代码随想录刷题复习day01

day01

数组-二分查找

class Solution {
    public int search(int[] nums, int target) {
        // 左闭右闭
        int left = 0;
        int right = nums.length - 1;
        int mid = 0;
        while (right >= left) {
            mid = left + (right - left) / 2;
            if (nums[mid] > target)
                right = mid - 1;
            else if (nums[mid] < target)
                left = mid + 1;
            else
                return mid;
        }
        return -1;

    }
}

数组要用[]

数组长度nums.length

中文分号

1.当nums[mid] != target时，应该更改区间范围，当前这个mid不应该考虑了，因为当前这个mid已经没有等于
target的可能性了**(左闭右闭的时候 right=mid不正确)**

2.考虑到算法逻辑上的合理性，在查找之前应该判断我们的目标元素在不在数组之中，不在的话直接返回-1，在的话才开始二分查找

// 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算
if (target < nums[0] || target > nums[nums.length - 1]) {
return -1;
}

3.(max- min) >> 1相当于(min + max) / 2

  if (nums[mid] > target)
                right = mid - 1;

链表-移除链表元素

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        ListNode dummyhead=new ListNode(-1);
        dummyhead.next=head;
        ListNode cur=dummyhead;
        while(cur.next!=null) {
            if(cur.next.val!=val) cur=cur.next;
            else cur.next=cur.next.next;
        }
        return dummyhead.next;
    }
}

1.移除是 cur.next=cur.next.next;而不是cur=cur.next.next;

2.定义虚拟头节点dummyhead统一操作

3.终止条件cur.next!=null，一直往下走是一个持续的过程用while

哈希表-有效字母异位词

定义一个存放26个小写字母的整数数组 int hash[26]

i=1，若索引1为字符’b’，则’b’-‘a’=1,则hash[1]++；hash索引1存放的是b出现的次数,最后比较数组 hash[26]时候
全0即可

class Solution {
    public boolean isAnagram(String s, String t) {
        int[] hash = new int[26];// 定义一个存放26个小写字母的整数数组hash
        if (s.length() == t.length()) {
            for (int i = 0; i < s.length(); i++) {
                hash[s.charAt(i) - 'a']++;
                hash[t.charAt(i) - 'a']--;
            }
        }
        else return false;
        for (int i = 0; i < 26; i++) {
            if (hash[i] != 0) {
                return false;
            }
        }
        return true;
    }
}

String类相关的API
s.charAt(i) 返回指定索引处char值
s.length() 返回字符串长度

字符串-反转字符串

取巧调用库函数

将字符数字遍历使用StringBuilder拼接然后reverse 再调用 s[i] = sb.charAt(i);

class Solution {
    public void reverseString(char[] s) {
        StringBuilder sb = new StringBuilder();
        for (char c : s) sb.append(c);
        sb.reverse();
        for (int i = 0; i < s.length; i++) {
            s[i] = sb.charAt(i);
        }
    }
}

如果一道题目使用库函数可以很简单的做出来，建议不要使用不然题目没啥意义

双指针

class Solution {
    public void reverseString(char[] s) {
        int left=0;
        int right=s.length-1;
        while(right>=left){
            char temp=s[left];
            s[left] = s[right];
            s[right] = temp;
            left++;
            right--;
        }
    }
}

栈与队列-用栈实现队列

class MyQueue {
    Stack<Integer> stackIn;
    Stack<Integer> stackOut;

    // 初始化两个栈
    public MyQueue() {
        stackIn = new Stack<>(); // 负责进栈
        stackOut = new Stack<>(); // 负责出栈
    }

    public void push(int x) {
        stackIn.push(x);// 压入入栈stackIn的栈顶
    }

    // pop 和push之前需要先判断栈是否为空
    public int pop() {
        // 一旦有输出操作，就需要把入栈内的元素全部压入出栈，然后在做相关操作
        while (!stackIn.empty()) {
            stackOut.push(stackIn.pop());
        }
        return stackOut.pop();
    }

    public int peek() {
        // 一旦有输出操作，就需要把入栈内的元素全部压入出栈，然后在做相关操作
        while (!stackIn.empty()) {
            stackOut.push(stackIn.pop());
        }
        return stackOut.peek();
    }

    public boolean empty() {
        // 两个栈为空才为空
        return (stackIn.empty() && stackOut.empty());
    }
}

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = new MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * boolean param_4 = obj.empty();
 */

一开始将stackIn 和 stackOut 在构造函数中被定义为局部变量，这样它们在构造函数结束时就会被销毁。应该将它们定义为类的成员变量。

在这里插入图片描述

二叉树1-二叉树的递归遍历

以下以前序遍历为例：

确定递归函数的参数和返回值：因为要打印出前序遍历节点的数值，所以参数里需要传入vector来放节点的数值，除了这一点就不需要再处理什么数据了也不需要有返回值，所以递归函数返回类型就是void，代码如下：

public void front(TreeNode root,List<Integer> res){//确定递归函数的参数及返回值

2.确定终止条件：在递归的过程中，如何算是递归结束了呢，当然是当前遍历的节点是空了，那么本层递归就要结束了，所以如果当前遍历的这个节点是空，就直接return，代码如下：

if(root==null) return;

3.确定单层递归的逻辑：前序遍历是中左右的顺序，所以在单层递归的逻辑，是要先取中节点的数值，代码如下：

//确定单层递归逻辑
    res.add(root.val);//中
    front(root.left,res);//左
    front(root.left,res);//右

单层递归的逻辑就是按照中左右的顺序来处理的，这样二叉树的前序遍历，基本就写完了，再看一下完整代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
// 前序遍历顺序：中-左-右 递归
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        front(root, res);
        return res;
    }
    public void front(TreeNode root,List<Integer> res){//确定递归函数的参数及返回值
    //确定终止条件
    if(root==null) return;
    //确定单层递归逻辑
    res.add(root.val);//中
    front(root.left,res);//左
    front(root.left,res);//右
    }
}

递归要严格按照三部曲来

res定义为全局变量，共同维护

搞清楚前序遍历为中-左-右

后序遍历：

public void back(TreeNode root, List<Integer> res) {// 1.确定递归函数的参数和返回值
if (root == null) return;// 2.确定终止条件
// 3.确定单层递归的逻辑
back(root.left, res);// 左
back(root.right, res);// 右
res.add(root.val);// 中
}

中序遍历:

public void mid(TreeNode root,List<Integer> res){// 1.确定递归函数的参数和返回值
if(root==null) return;// 2.确定终止条件
// 3.确定单层递归的逻辑
mid(root.left,res);//左
res.add(root.val);//中
mid(root.right,res);//右
}

回溯-组合

回溯基本介绍
递归+for循环
回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案
回溯可以解决哪些问题？
组合、切割、子集、排列、棋盘问题
如何理解回溯法？
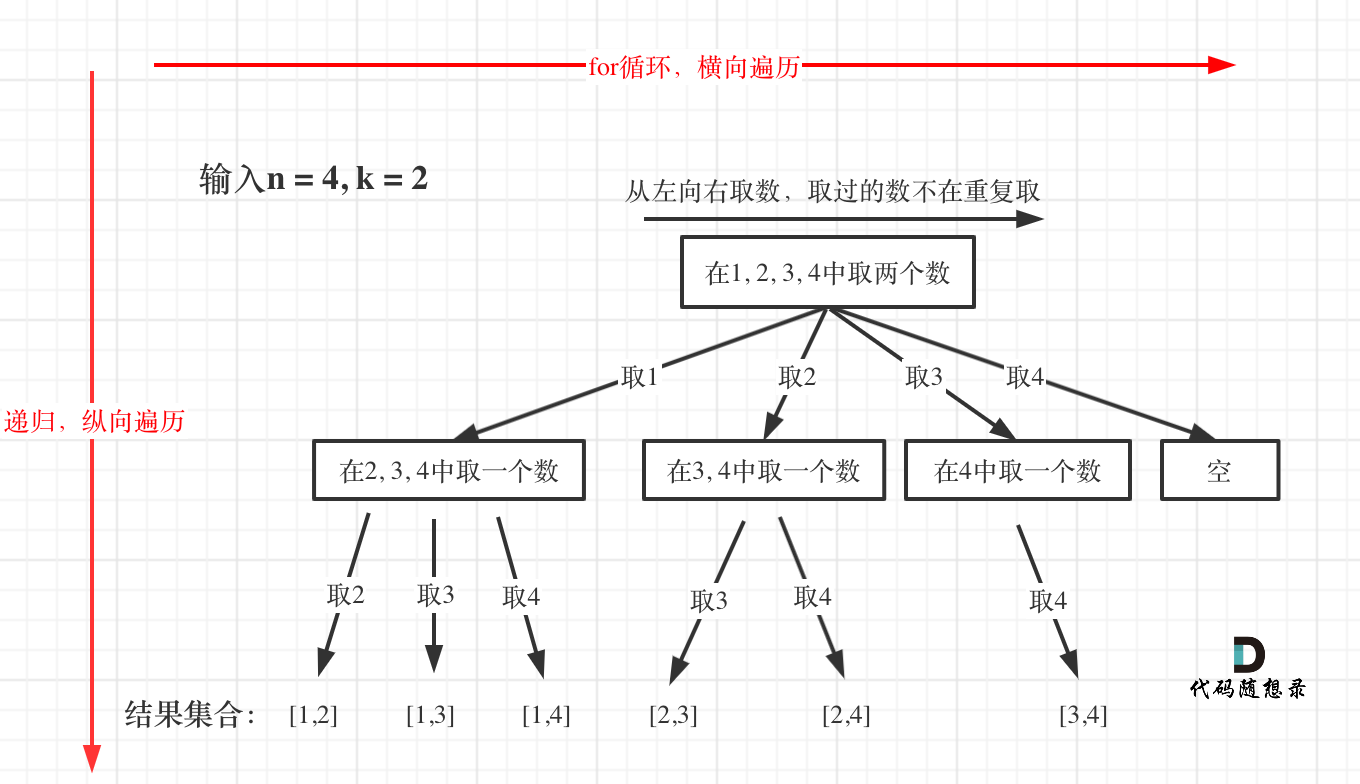
抽象成一种图形结构，所有的回溯法都可以抽象成一个树形结构（N叉树）
回溯算法通过递归来控制有多少层for循环，递归里的每一层就是一个for循环

严格按照回溯三部曲来

回溯法的搜索过程就是一个树型结构的遍历过程，在如下图中，可以看出for循环用来横向遍历，递归的过程是纵向遍历

77.组合1

class Solution {
    public List<List<Integer>> combine(int n, int k) {
        LinkedList<Integer> path = new LinkedList<>();// 用于存放符合条件的单一结果
        List<List<Integer>> res = new ArrayList<>();// 用于存放最后的结果集
        backtracking(n,k,1);
        return res;
    }

    void backtracking(int n, int k, int startIndex) { // 1.确定递归参数及返回值
        // path这个数组的大小如果达到k，说明我们找到了一个子集大小为k的组合了，在图中path存的就是根节点到叶子节点的路径。
        if (path.size() == k) { // 2.回溯函数终止条件
            res.add(new ArrayList<>(path));
            return;
        }
        // 3.单层递归逻辑
        for (int i = startIndex; i <= n; i++) {
            path.add(i);
            backtracking(n, k, i + 1);//递归下一层
            path.removeLast();//回溯的操作了，撤销本次处理的结果
        }

    }
}

1.path 和 res 应该是类的成员变量，这样在递归调用过程中可以正确地共享和更新它们。

2.res 的类型应该是 List<List<Integer>>，这样可以匹配 combine 方法的返回类型。

3.大多数剪枝操作都在for循环中的i的范围做文章的

for(int i=startIndex; i<=n-(k-path.size())+1;i++)

77.组合4

4.在回溯过程中不能直接将 path 添加到 res，这样没有创建 path 的副本。这会导致 res 中的所有列表元素最终都引用同一个 path 对象。因此，最后 res 中的所有元素都会是相同的，且等于最后一个 path 的状态

5.注意startIndex，代表下一层递归的起始搜索位置

二叉树2-二叉树的迭代遍历

我们先看一下前序遍历。

前序遍历是中左右，每次先处理的是中间节点，那么先将根节点放入栈中，然后将右孩子加入栈，再加入左孩子。

为什么要先加入右孩子，再加入左孩子呢？因为这样出栈的时候才是中左右的顺序。

动画如下：

二叉树前序遍历（迭代法）

// 前序遍历顺序：中-左-右，入栈顺序：中-右-左
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();// 定义一个栈用于存放节点
        stack.push(root);//把根节点压入栈
        while (!stack.isEmpty()) {// 非空时执行
            TreeNode node = stack.pop();//中节点出栈才会将子节点压入栈
            res.add(node.val);// 中
            if (node.right != null) {
                stack.push(node.right);// 右节点压入栈
            }
            if (node.left != null) {
                stack.push(node.left);// 左节点压入栈
            }
        }
        return res;
    }
}

后序

// 后序遍历顺序 左-右-中 入栈顺序：中-左-右 出栈顺序：中-右-左， 最后翻转结果
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();// 定义一个栈用于存放节点
        stack.push(root);//把根节点压入栈
        while (!stack.isEmpty()) {// 非空时执行
            TreeNode node = stack.pop();//中节点出栈才会将子节点压入栈
            res.add(node.val);// 中
            if (node.left != null) {// 左节点压入栈
                stack.push(node.left);
            }
            if (node.right != null) {// 右节点压入栈
                stack.push(node.right);
            }
        }
        Collections.reverse(res);//调用 Collections工具类反转数组
        return res;
    }
}

在这里插入图片描述

中序

中序：左右中

分析一下为什么刚刚写的前序遍历的代码，不能和中序遍历通用呢，因为前序遍历的顺序是中左右，先访问的元素是中间节点，要处理的元素也是中间节点，所以刚刚才能写出相对简洁的代码，因为要访问的元素和要处理的元素顺序是一致的，都是中间节点。

那么再看看中序遍历，中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了处理顺序和访问顺序是不一致的。

那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。

动画如下：

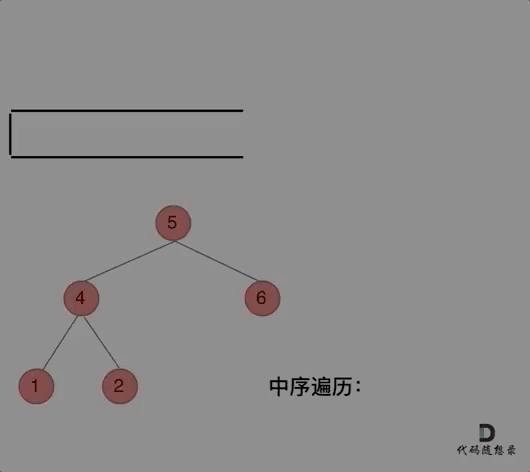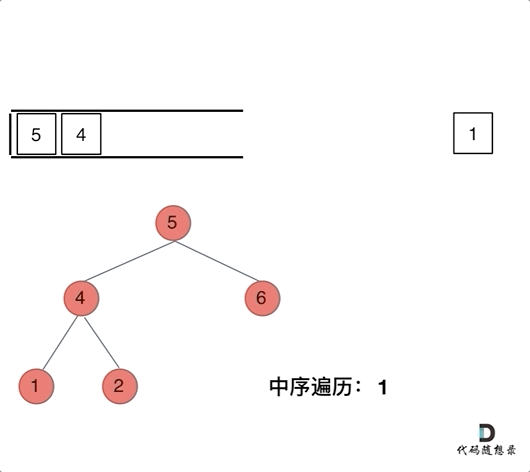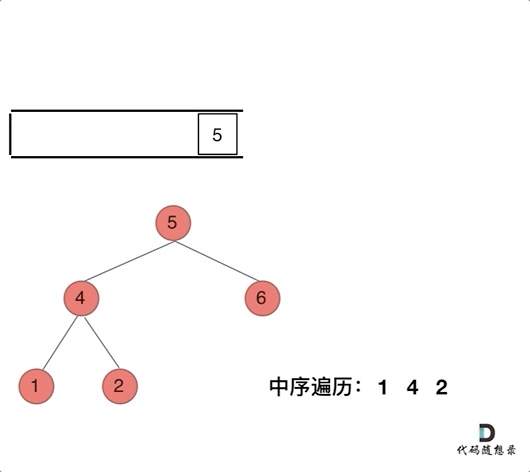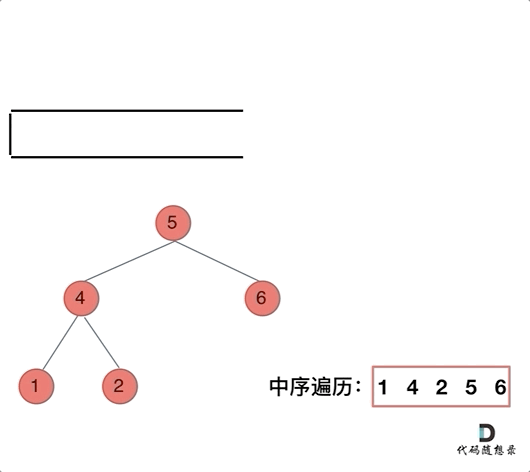
二叉树中序遍历（迭代法）

先中节点左节点全部加进去，然后逐个弹出做处理

指针 cur 从根节点开始，沿着左子树不断深入，当无法继续深入时，从栈中弹出节点，记录节点值，然后转向右子树。

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        
        while (cur != null || !stack.isEmpty()) {
            if (cur != null) {
                stack.push(cur); // 将访问的节点放进栈
                cur = cur.left;  // 左
            } else {
                cur = stack.pop(); // 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）
                result.add(cur.val); // 中
                cur = cur.right;     // 右
            }
        }
        
        return result;
    }
}

二叉树3-二叉树的层序遍历

层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。

需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。

而这种层序遍历方式就是图论中的广度优先遍历，只不过我们应用在二叉树上。

使用队列实现二叉树广度优先遍历，动画如下：

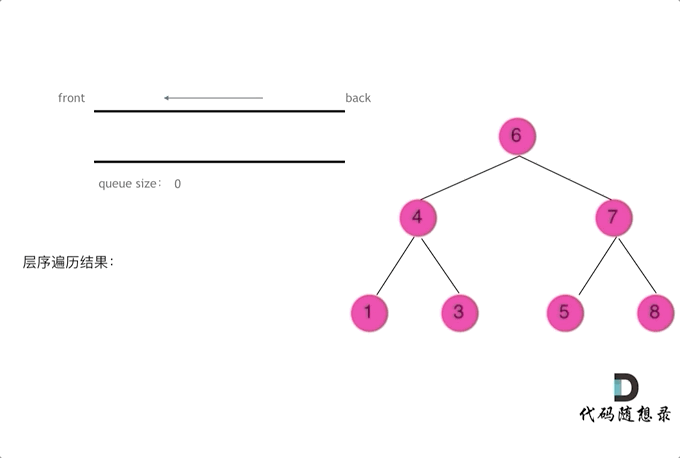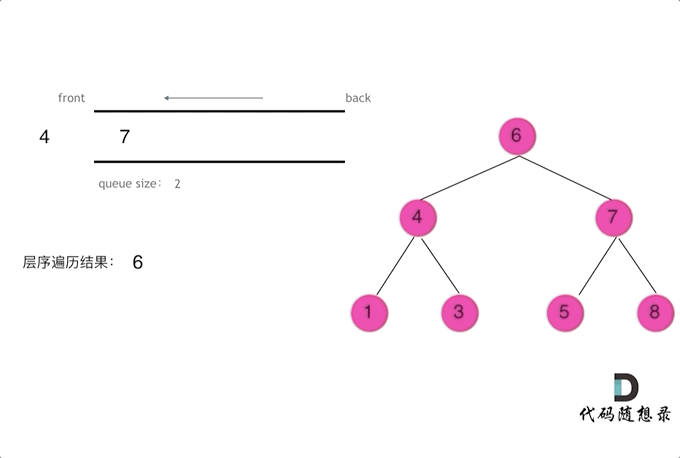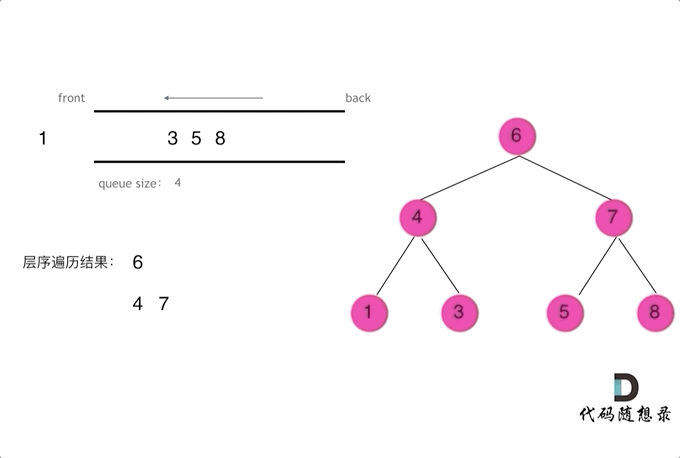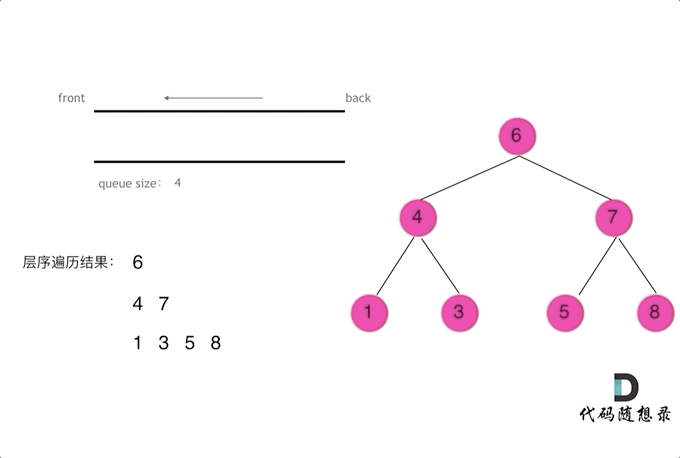
102二叉树的层序遍历

这样就实现了层序从左到右遍历二叉树。

代码如下：这份代码也可以作为二叉树层序遍历的模板

简洁形式

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) {
            return res; // 如果根节点为空，直接返回空的结果列表
        }
        Queue<TreeNode> que = new LinkedList<>();//双端队列
        que.offer(root); // 将根节点加入到队列中

        while(!que.isEmpty()){//非空时执行
         List<Integer> itemList = new ArrayList<>(); // 当前层的节点值列表
        int len=que.size();

        for(int i=1;i<=len;i++){
            TreeNode tempNode=que.poll();
            itemList.add(tempNode.val);
            if(tempNode.left!=null) que.offer(tempNode.left);
            if(tempNode.right!=null) que.offer(tempNode.right);
        }
        res.add(itemList);//将当前层的节点值列表加入到结果列表中
        }
        return res;
    }
}

为空的时候返回[]；而不是null；

因为是每一层遍历的时候都生成了一个itemList；所以后面可以直接res.add（itemList）

Queue

在这里插入图片描述

贪心-分发饼干

贪心算法一般分为如下四步：
1.将问题分解为若干个子问题
2.找出适合的贪心策略
3.求解每一个子问题的最优解
4.将局部最优解堆叠成全局最优解
这个四步其实过于理论化了，我们平时在做贪心类的题目很难去按照这四步去思考，真是有点“鸡肋”。
做题的时候，只要想清楚 局部最优是什么，如果推导出全局最优，其实就够了。

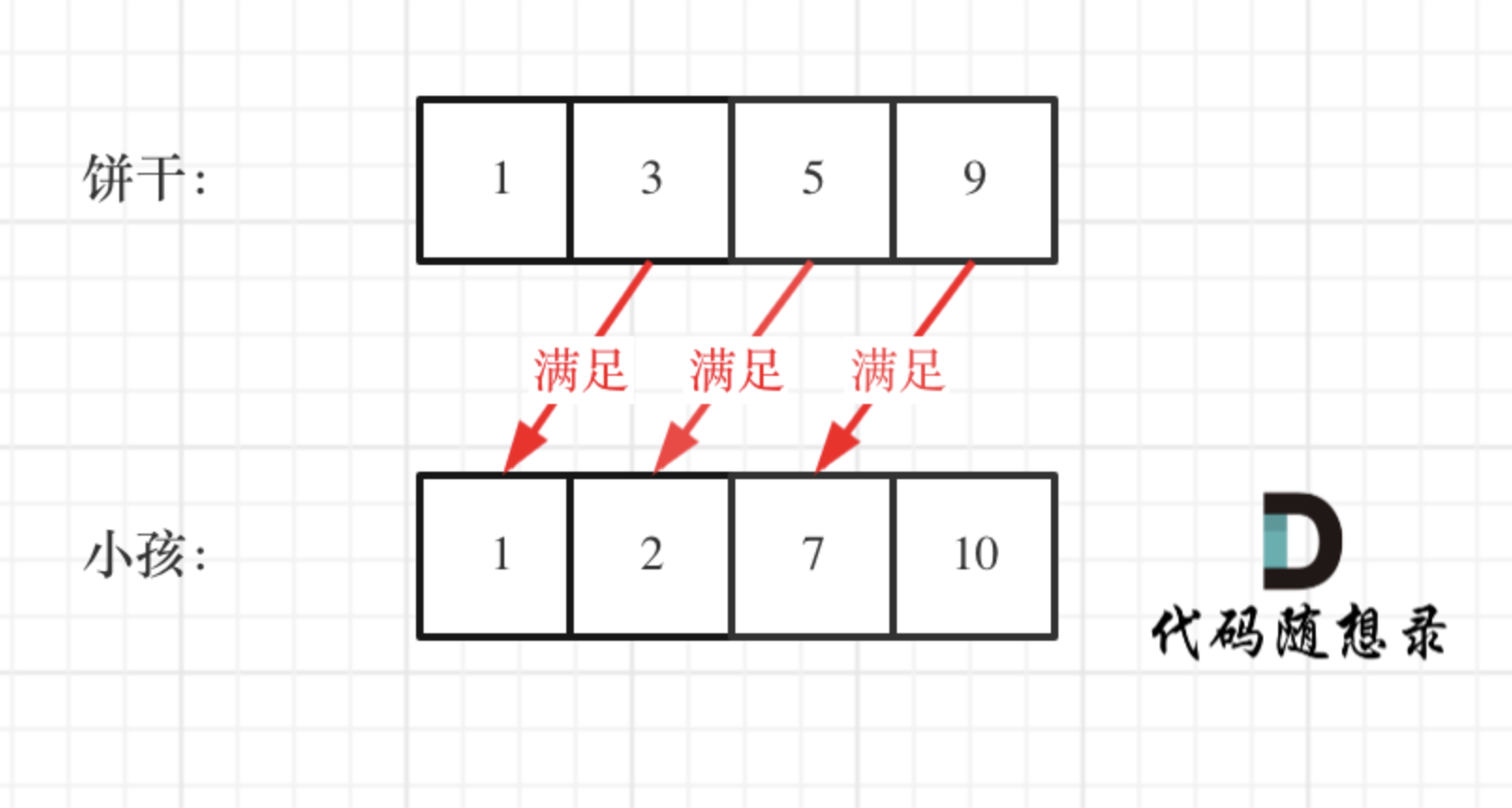
class Solution {
    // 思路2：优先考虑胃口，先喂饱大胃口     
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);//胃口
        Arrays.sort(s);//饼干尺寸
        int count = 0;
        int start = s.length - 1;
        // 遍历胃口   for 控制 胃口，里面的 if 控制饼干。
        for (int index = g.length - 1; index >= 0; index--) {
            if (start >= 0 && g[index] <= s[start]) {
                start--;
                count++;
            }
        }
        return count;
    }
}

动态规划1-斐波那契数

动规五部曲

动规五部曲：
这里我们要用一个一维dp数组来保存递归的结果
1.确定dp数组以及下标的含义
dp[i]的定义为：第i个数的斐波那契数值是dp[i]
2.确定递推公式
为什么这是一道非常简单的入门题目呢？
因为题目已经把递推公式直接给我们了：状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
3.dp数组如何初始化
题目中把如何初始化也直接给我们了，如下：
4.确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，dp[i]是依赖 dp[i - 1] 和 dp[i - 2]，那么遍历的顺序一定是从前到
后遍历的
5.举例推导dp数组
按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2]，我们来推导一下，当N为10的时候，dp数组应该是如下的数列：
0 1 1 2 3 5 8 13 21 34 55

class Solution {
    public int fib(int n) {
        if (n <= 1)
            return n;
        int[] dp = new int[n + 1];//一定是n+1个数，因为有一个0
        dp[0] = 0;
        dp[1] = 1;
        for (int index = 2; index <= n; index++) {
            dp[index] = dp[index - 1] + dp[index - 2];
        }
        return dp[n];
    }
}

//一定是n+1个数，因为有一个0

动态规划2-爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

1.确定dp数组以及下标的含义

dp[i]：爬到第i层楼梯，有dp[i]种方法

2.确定递推公式

如何可以推出dp[i]呢？

从dp[i]的定义可以看出，dp[i] 可以有两个方向推出来。

首先是dp[i - 1]，上i-1层楼梯，有dp[i - 1]种方法，那么再一步跳一个台阶不就是dp[i]了么。

还有就是dp[i - 2]，上i-2层楼梯，有dp[i - 2]种方法，那么再一步跳两个台阶不就是dp[i]了么。

那么dp[i]就是 dp[i - 1]与dp[i - 2]之和！

所以dp[i] = dp[i - 1] + dp[i - 2] 。

在推导dp[i]的时候，一定要时刻想着dp[i]的定义，否则容易跑偏。

这体现出确定dp数组以及下标的含义的重要性！

3.dp数组如何初始化

再回顾一下dp[i]的定义：爬到第i层楼梯，有dp[i]种方法。

那么i为0，dp[i]应该是多少呢，这个可以有很多解释，但基本都是直接奔着答案去解释的。

例如强行安慰自己爬到第0层，也有一种方法，什么都不做也就是一种方法即：dp[0] = 1，相当于直接站在楼顶。

但总有点牵强的成分。

那还这么理解呢：我就认为跑到第0层，方法就是0啊，一步只能走一个台阶或者两个台阶，然而楼层是0，直接站楼顶上了，就是不用方法，dp[0]就应该是0.

其实这么争论下去没有意义，大部分解释说dp[0]应该为1的理由其实是因为dp[0]=1的话在递推的过程中i从2开始遍历本题就能过，然后就往结果上靠去解释dp[0] = 1。

从dp数组定义的角度上来说，dp[0] = 0 也能说得通。

需要注意的是：题目中说了n是一个正整数，题目根本就没说n有为0的情况。

所以本题其实就不应该讨论dp[0]的初始化！

我相信dp[1] = 1，dp[2] = 2，这个初始化大家应该都没有争议的。

所以我的原则是：不考虑dp[0]如何初始化，只初始化dp[1] = 1，dp[2] = 2，然后从i = 3开始递推，这样才符合dp[i]的定义。

class Solution {
    // 常规方式
    public int climbStairs(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

单调栈-每日温度

请根据每日气温列表，重新生成一个列表。对应位置的输出为：要想观测到更高的气温，至少需要等待的天数。如果气温在这之后都不会升高，请在该位置用 0 来代替。

例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。

//单调栈：适合求解当前元素左边或者右边第一个比当前元素大/小的元素。强调找到

递增：找第一个比他大的

递减：找第一个比他小的

栈内存放下标，记录我们遍历过的元素，然后和当前遍历的元素作对比T[i] ？T[st.pop()]

思路

在这里插入图片描述

情况一：当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
情况二：当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
情况三：当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况

class Solution {
    // 版本 1
    public int[] dailyTemperatures(int[] temperatures) {

        int lens = temperatures.length;
        int[] res = new int[lens];

        /**
         * 如果当前遍历的元素 大于栈顶元素，表示 栈顶元素的 右边的最大的元素就是 当前遍历的元素，
         * 所以弹出 栈顶元素，并记录
         * 如果栈不空的话，还要考虑新的栈顶与当前元素的大小关系
         * 否则的话，可以直接入栈。
         * 注意，单调栈里 加入的元素是 下标。
         */
        Deque<Integer> stack = new LinkedList<>();
        stack.push(0);
        for (int i = 1; i < lens; i++) {

            if (temperatures[i] <= temperatures[stack.peek()]) { // 当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况，直接加入
                stack.push(i);
            } else {
                while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
                    res[stack.peek()] = i - stack.peek();// 当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况，表示栈顶元素的右边的最大的元素就是当前遍历的元素，所以弹出栈顶元素，并记录
                    stack.pop();
                }
                stack.push(i);
            }
        }

        return res;
    }
}

多态：

Deque<Integer> stack=new LinkedList<>();

Deque<Integer> stack = new LinkedList<>(); 确实是一个多态的例子。在Java中，多态性（Polymorphism）是指对象可以表现为多种形态，这通常通过继承和接口实现。在这个例子中，Deque 是一个接口，而 LinkedList 是一个实现了 Deque 接口的具体类。

具体分析如下：

接口和实现：Deque 是一个接口，定义了双端队列的行为。LinkedList 是一个类，实现了 Deque 接口（以及其他接口如 List 和 Queue），并提供了具体的实现。
多态性：通过使用 Deque<Integer> stack，你可以将任何实现了 Deque 接口的类的实例赋值给 stack。在这个例子中，stack 被赋值为 LinkedList<Integer> 的实例，但它也可以是其他实现了 Deque 接口的类的实例，如 ArrayDeque<Integer>。这种设计允许代码更加灵活和可扩展，因为你可以在不改变代码其他部分的情况下，改变 stack 的具体实现。
面向接口编程：这是一种良好的编程实践，称为面向接口编程。通过依赖接口而不是具体实现，代码变得更具灵活性和可维护性。

如何判断是递增还是递减的单调栈呢？

递增：找第一个比他大的

递减：找第一个比他小的

栈内存放下标，记录我们遍历过的元素，然后和当前遍历的元素作对比T[i] ？T[st.pop()]

图论-所有可能路径

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

示例 1：

输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

private List<List<Integer>> result = new ArrayList<>(); // 收集符合条件的路径
private List<Integer> path = new ArrayList<>(); // 0节点到终点的路径

DFS深度优先搜索

1.确认递归函数，参数

首先我们dfs函数一定要存一个图，用来遍历的，还要存一个目前我们遍历的节点，定义为x,下标

至于单一路径，和路径集合可以放在全局变量，那么代码是这样的：

private List<List<Integer>> result = new ArrayList<>(); // 收集符合条件的路径
private List<Integer> path = new ArrayList<>(); // 0节点到终点的单一路径
    // x：目前遍历的节点
    // graph：存当前的图
    private void dfs(int[][] graph, int x)

2.确认终止条件

什么时候我们就找到一条路径了？

当目前遍历的节点为最后一个节点的时候，就找到了一条，从出发点到终止点的路径。

当前遍历的节点，我们定义为x，最后一点节点，就是 graph.length - 1（因为题目描述是找出所有从节点 0 到节点 n-1 的路径并输出）。

所以但 x 等于 graph.size() - 1 的时候就找到一条有效路径。代码如下：

  // 要求从节点 0 到节点 n-1 的路径并输出，所以是 graph.length - 1
        if (x == graph.length - 1) { // 找到符合条件的一条路径
            result.add(new ArrayList<>(path));// 收集有效路径
            return;
        }

3.处理目前搜索节点出发的路径

接下来是走当前遍历节点x的下一个节点。

首先是要找到 x节点链接了哪些节点呢？遍历方式是这样的：

 for (int i = 0; i < graph[x].length; i++) { // 遍历节点n链接的所有节点

接下来就是将选中的x所连接的节点，加入到单一路径来。

path.add(graph[x][i]); // 遍历到的节点加入到路径中来

一些录友可以疑惑这里如果找到x 链接的节点的，例如如果x目前是节点0，那么目前的过程就是这样的：

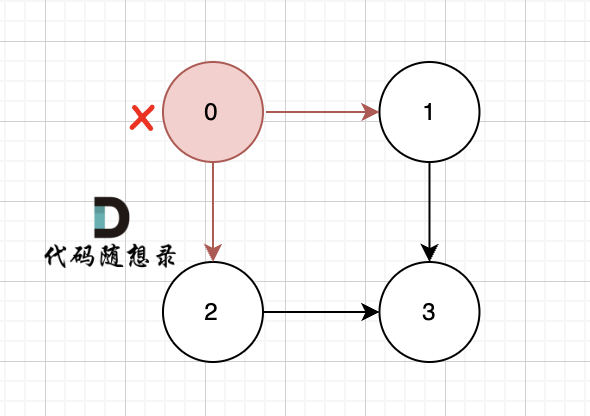
二维数组中，graph[x] [i] 都是x链接的节点，当前遍历的节点就是 graph[x][i] 。

进入下一层递归

dfs(graph, graph[x][i]); // 进入下一层递归

最后就是回溯的过程，撤销本次添加节点的操作。该过程整体代码：

 for (int i = 0; i < graph[x].length; i++) { // 遍历节点n链接的所有节点
            path.add(graph[x][i]); // 遍历到的节点加入到路径中来
            dfs(graph, graph[x][i]); // 进入下一层递归
            path.remove(path.size() - 1); // 回溯，撤销本节点
          //或者这么写： path.removeLast(); // 回溯，撤销本节点
        }

DFS

//dfs
class Solution {
    private List<List<Integer>> result = new ArrayList<>(); // 收集符合条件的路径
    private List<Integer> path = new ArrayList<>(); // 0节点到终点的路径

    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        path.add(0); // 无论什么路径已经是从0节点出发
        dfs(graph, 0); // 开始遍历
        return result;
    }

    // x：目前遍历的节点
    // graph：存当前的图
    private void dfs(int[][] graph, int x) {
        // 要求从节点 0 到节点 n-1 的路径并输出，所以是 graph.length - 1
        if (x == graph.length - 1) { // 找到符合条件的一条路径//   从0---->3
            result.add(new ArrayList<>(path));// 收集有效路径
            return;
        }
        for (int i = 0; i < graph[x].length; i++) { // 遍历节点n链接的所有节点
            path.add(graph[x][i]); // 遍历到的节点加入到路径中来 0->1  //21行回来 变成0->1->3 r 到了15行 result加入0->1->3路径 return回21，撤销
            dfs(graph, graph[x][i]); // 进入下一层递归 进入节点1
            path.removeLast(); // 回溯，撤销本节点
        }
    }
}