0、前言

动态矩阵控制（Dynamic Matrix Control，DMC）是一种典型的模型预测控制方法，其不需要被控对象的数学模型，只需要获取被控对象的阶跃响应序列即可实现控制效果，但其需要被控对象是渐近稳定的。

1、稳定 SISO 系统的阶跃响应模型

考虑单输入单输出（Signal Input Signal Output，SISO）系统，其传递函数为
$$G(s)=\frac{y(s)}{u(s)}\text{\hspace{1em}(1)}$$

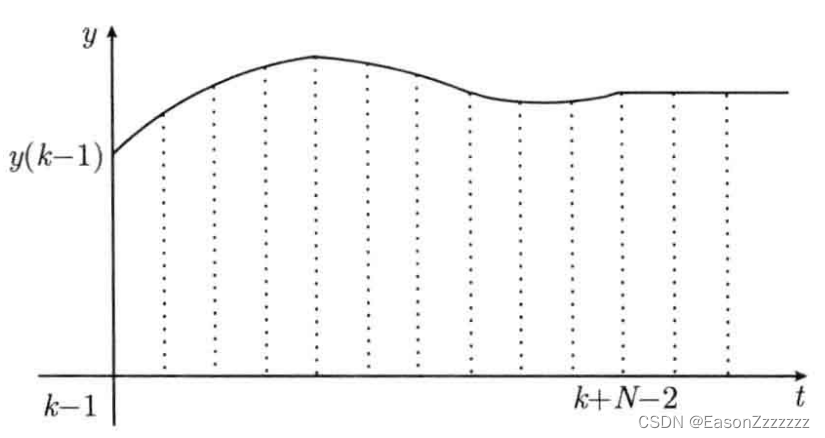
首先考虑当输入不变时，系统的非零初始状态响应
如图所示（系统过渡过程时间为 $N$ 个采样间隔）

系统在 $k+N-2$ 以后进入稳态，输出保持不变，定义 $k-1$ 时刻的未来 $N$ 步输出为
$$Y(k-1)=\left\{\begin{array}{c}{\left[\begin{array}{ccccc}y(k-1)& y(k)& \cdots & y(k+N-3)& y(k+N-2)\end{array}\right]}^T\\ \Delta u(k+i)=0,i=-1,0,\cdots ,N-2\end{array}\right\}\text{\hspace{1em}(2)}$$

我们称 $Y(k-1)$ 为系统在 $k-1$ 时刻的 “ 状态 ”。它的物理意义为：在输入不变条件下系统的非零初始状态响应的 $N$ 步输出，即系统无外部输入的 “ 自由响应 ” 的 $N$ 步输出为状态变量的 $N$ 个分量。

因此定义 $k$ 时刻的状态变量为
$$Y(k)=\left\{\begin{array}{c}{\left[\begin{array}{ccccc}y(k)& y(k+1)& \cdots & y(k+N-2)& y(k+N-1)\end{array}\right]}^T\\ \Delta u(k+i)=0,i=0,1,\cdots ,N-1\end{array}\right\}\text{\hspace{1em}(3)}$$

当 $\Delta u(k-1)=0$ 时 $Y(k)$ 与 $Y(k-1)$ 之间的关系为
$$Y(k)=M_{ss}Y(k-1)\text{\hspace{1em}(4)}$$

其中
$$M_{ss}=\left[\begin{array}{cccccc}0& 1& 0& \cdots & 0& 0\\ 0& 0& 1& \cdots & 0& 0\\ ⋮& ⋮& ⋮& & ⋮& ⋮\\ 0& 0& 0& \cdots & 0& 1\\ 0& 0& 0& \cdots & 0& 1\end{array}\right]\text{\hspace{1em}(5)}$$

这就是稳定 SISO 系统的不变输入非零初始状态响应。

接着考虑当初始状态为零时，系统的输入响应
在系统平衡状态下做一个单位阶跃响应实验，得到系统的输出响应如图所示。

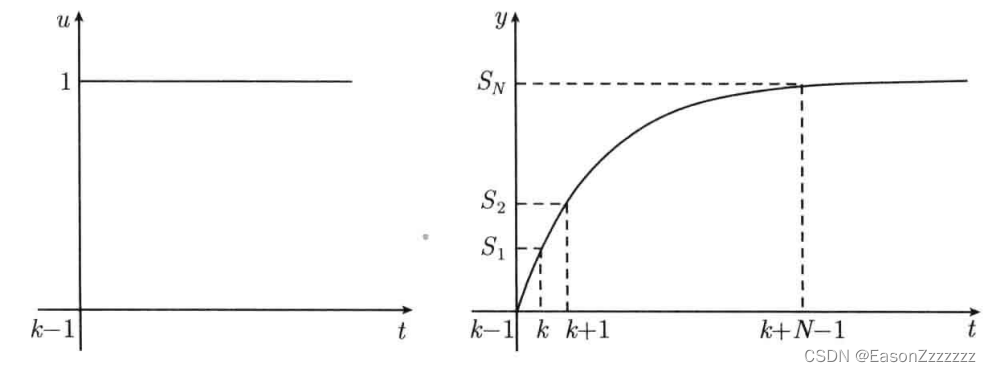
采样得到系统零初始条件下单位阶跃响应序列为
{ 0 , s 1 , s 2 , ⋯   , s N , s N , ⋯   } (6) \lbrace 0,s_1,s_2,\cdots,s_N,s_N,\cdots\rbrace\tag{6} {0,s1​,s2​,⋯,sN​,sN​,⋯}(6)

由线性系统的齐次性，对任意的输入变化 $\Delta u(k-1)$，系统的响应序列为
{ 0 , s 1 , s 2 , ⋯   , s N , s N , ⋯   } ⋅ Δ u ( k − 1 ) (6) \lbrace 0,s_1,s_2,\cdots,s_N,s_N,\cdots\rbrace\cdot\Delta u(k-1)\tag{6} {0,s1​,s2​,⋯,sN​,sN​,⋯}⋅Δu(k−1)(6)

记单位阶跃响应系数矩阵为
$$S={\left[\begin{array}{c}{s}_1\\ s_2\\ ⋮\\ s_N\end{array}\right]}_{N\times 1}\text{\hspace{1em}(7)}$$

则零初始状态下，系统对任意输入的响应可以描述为
$$Y(k)=S\Delta u(k-1)\text{\hspace{1em}(8)}$$

由于线性系统满足叠加性，因此，由（4）和（8）得到，在非零初始状态下系统对任意输入变化的响应为
$$\boxed{Y(k)=M_{ss}Y(k-1)+S\Delta u(k-1)}\text{\hspace{1em}(9)}$$

其中初始条件为
$$Y(0)={\left[\begin{array}{c}y(0)\\ ⋮\\ y(0)\end{array}\right]}_{N\times 1}\text{\hspace{1em}(10)}$$

而系统在 $k$ 时刻的输出为
$$\boxed{y(k)=CY(k)}\text{\hspace{1em}(11)}$$

其中
$$C={\left[\begin{array}{cccc}1& 0& \cdots & 0\end{array}\right]}_{1\times N}\text{\hspace{1em}(12)}$$

综上，（9）和（11）就是系统的单位阶跃响应模型。

2、SISO 系统的动态矩阵控制（DMC）

2.1、被控系统描述

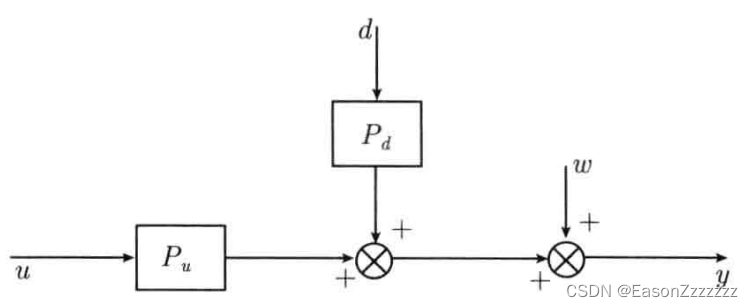
如图所示为被控系统，$u$ 为控制输入，$y$ 为输出，$d$ 为可以测量的外部干扰，$w$ 为不能测量的外部干扰，$P_u$ 为输入 $u$ 到输出 $y$ 的传递函数，$P_d$ 为可测量干扰 $d$ 到输出 $y$ 的传递函数。设控制输入 $u$ 和可测量干扰 $d$ 对输出 $y$ 的单位阶跃响应系数矩阵分别为
$$S_u=\left[\begin{array}{c}{s}_1^u\\ s_2^u\\ ⋮\\ s_N^u\end{array}\right],S_d=\left[\begin{array}{c}{s}_1^d\\ s_2^d\\ ⋮\\ s_N^d\end{array}\right],\text{\hspace{1em}(13)}$$

由于线性系统满足齐次性和叠加性，因此，由（9）可以得出带可测干扰的单位阶跃响应模型为
$$\begin{array}{rl}Y(k)& =M_{ss}Y(k-1)+S_u\Delta u(k-1)+S_d\Delta d(k-1)\\ y(k)& =CY(k)\end{array}\text{\hspace{1em}(14)}$$

2.2、状态估计

由于单位阶跃响应模型（14）的状态不是全部可以测量的（只有第一个分量是可以测量的）。因此，需要对状态进行估计，用估计的状态作为初始条件预测系统未来的动态。

在 $k-1$ 时刻，由（14）计算 $k$ 时刻的状态，记为 $Y(k|k-1)$，即
$$Y(k|k-1)=M_{ss}\hat{Y}(k-1)+S_u\Delta u(k-1)+S_d\Delta d(k-1)\text{\hspace{1em}(15)}$$

其中，$\hat{Y}(k-1)$ 是 $k-1$ 时刻对状态的估计。计算 $k$ 时刻的输出为
$$y(k|k-1)=CY(k|k-1)\text{\hspace{1em}(16)}$$

在 $k$ 时刻的测量值为 $y(k)$，与计算值之差为 $y(k)-y(k|k-1)$。以这个误差作为校正量，得到校正后的状态分量如下：
$$\begin{array}{rl}\hat{y}(k|k)& =y(k|k-1)+[y(k)-y(k|k-1)],\\ \hat{y}(k+1|k)& =y(k+1|k-1)+[y(k)-y(k|k-1)],\\ ⋮,& \\ \hat{y}(k+N-1|k)& =y(k+N-1|k-1)+[y(k)-y(k|k-1)].\end{array}\text{\hspace{1em}(17)}$$

记
$$\hat{Y}(k)={\left[\begin{array}{c}\hat{y}(k|k)\\ \hat{y}(k+1|k)\\ ⋮\\ \hat{y}(k+N-1|k)\end{array}\right]}_{N\times 1}\text{\hspace{1em}(18)}$$

则上式变为
$$\hat{Y}(k)=Y(k|k-1)+K_I(y(k)-y(k|k-1)),其中K_I={\left[\begin{array}{c}1\\ ⋮\\ 1\end{array}\right]}_{N\times 1}\text{\hspace{1em}(19)}$$

将（15）和（16）代入（19），得
$$\begin{array}{rl}\hat{Y}(k)& =Y(k|k-1)+K_I(y(k)-y(k|k-1))\\ & =(I-K_{I}C)Y(k|k-1)+K_{I}y(k)\\ & =(I-K_{I}C)M_{ss}\hat{Y}(k-1)+K_{I}y(k)+(I-K_{I}C)S_u\Delta u(k-1)+(I-K_{I}C)S_d\Delta d(k-1)\end{array}\text{\hspace{1em}(20)}$$

这是一个典型的状态估计器方程，其中
$$(I-K_{I}C)M_{ss}={\left[\begin{array}{cccccc}0& 0& 0& 0& \cdots & 0\\ 0& -1& 1& 0& \cdots & 0\\ 0& -1& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮& & ⋮\\ 0& -1& 0& 0& \cdots & 1\\ 0& -1& 0& 0& \cdots & 1\end{array}\right]}_{N\times N}\text{\hspace{1em}(21)}$$

可以证明，$(I-K_{I}C)M_{ss}$ 的所有特征值均位于单位圆内，因此，估计器（20）是名义渐近稳定的。

3、预测方程

采用 基于状态空间模型的无约束预测控制 相同的方法推导预测方程。

对系统未来 $p$ 步输出的预测可以由下面的预测方程计算：
$$Y_p(k+1|k)=\mathcal{M}\hat{Y}(k)+{\mathcal{S}}_u\Delta U(k)+{\mathcal{S}}_d\Delta d(k)$$

其中，
$$\begin{array}{rl}& \mathcal{M}={\left[\begin{array}{ccccccccc}0& C_c& 0& 0& 0& \cdots & 0& \cdots & 0\\ 0& 0& C_c& 0& 0& \cdots & 0& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& & ⋮\\ 0& 0& \cdots & 0& C_c& \cdots & 0& \cdots & 0\end{array}\right]}_{p\times N}\\ & {\mathcal{S}}_d={\left[\begin{array}{c}{C}_c{S}_1^d\\ C_c{S}_2^d\\ ⋮\\ C_c{S}_p^d\end{array}\right]}_{p\times 1}\\ & {\mathcal{S}}_u={\left[\begin{array}{ccccc}{C}_c{S}_1^u& 0& 0& \cdots & 0\\ C_c{S}_2^u& C_c{S}_1^u& 0& \cdots & 0\\ ⋮& ⋮& ⋮& & ⋮\\ C_c{S}_m^u& C_c{S}_{m-1}^u& \cdots & \cdots & C_c{S}_1^u\\ ⋮& ⋮& ⋮& & ⋮\\ C_c{S}_p^u& C_c{S}_{p-1}^u& \cdots & \cdots & C_c{S}_{p-m+1}^u\end{array}\right]}_{p\times m}\end{array}$$