前言
作为电子系统必不可少的信号源,在很大程度上决定了系统的性能, 因而常称之为电子系统的“心脏”。传统的信号源采用振荡器, 只能产生少数几种波形,自动化程度较低,且仪器体积大,灵活性与准确度差。而现在要求信号源能产生波形的种类多、频率高,而且还要体积小、可靠性高、操作灵活、使用方便及可由计算机控制。
直接数字频率合成(DDS)是近年来发展起来的一种新的频率合成技术,其主要优点是相对带宽很大,频率转换时间极短(可小于20 ns),频率分辨率很高,全数字化结构便于集成,输出相位连续可调,且频率、相位和幅度均可实现程控。
DDS建立在采样定理基础上,首先对需要产生的波形进行采样,将采样值数字化后存入存储器作为查找表,然后通过查表读取数据,再经D/A转换器转换为模拟量,将保存的波形重新合成出来。DDS与基于PLL的频率合成器相比具有简便、精确、快速、廉价和灵活等优点。
DDS 能够与计算机技术紧密结合在一起,克服了模拟频率合成和锁相频率合成等传统频率合成技术电路复杂、设备体积较大、成本较高的不足,因此它是一种很有发展前途的频率合成技术。DDS 技术现已在接收机本振、信号发生器、通信系统、雷达系统等方面得到广泛应用。数字频率合成器作为一种信号产生装置己经越来越受到人们的重视,它可以根据用户的要求产生相应的波形,具有重复性好、实时性强等优点,己经逐步取代了传统的函数发生器。本文的目的是设计开发出一个能产生正弦波的信号源,直接数字频率合成技术是研制该系统的关键技术。
1 系统设计
1.1设计要求
技术指标:
(1)输出波形:正弦函数(改变存储器波形数据可实现任意函数波形发生器)。
(2)输出电压峰峰值:10V。
(3)输出频率:80Hz—5120Hz
(4)分辨率:80Hz
二个按钮分别用来选择增减频率字。
四个数码管显示输出的当前频率。
1.2方案论证
DDS基本原理框图如图1.2.1所示:它主要由相位累加器、波形存储器、D/A 转换器和低通滤波器构成。
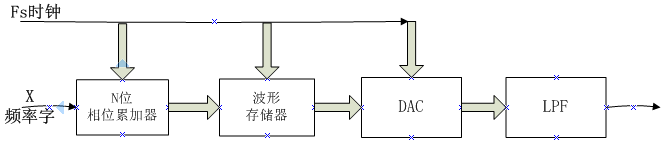
图1.2.1
DDS 工作时,在时钟脉冲Fs的控制下对频率控制字X 用累加器进行处理以得到相应的相位码,然后由相位码寻址波形存储器进行相位码―幅度编码变换,再经过D/A 数模变换器得到相应的阶梯波,最后经过低通滤波器对阶梯波进行平滑处理即可得到由频率控制字X决定的频率可调的输出波形。参考频率源一般是高稳定的晶体振荡器,用于DDS 中各部件的同步工作,因此DDS 输出的合成信号频率稳定度与晶体振荡器是相同的。在标准频率参考源的控制下,频率控制字X可决定相应的相位增量,相位累加器则以步长X进行线性累加,相位累加器积满时就会产生一次溢出,从而完成一个周期性动作,这个动作周期即是DDS合成信号的一个周期。
在使用FPGA 设计DDS 时,要在满足系统要求和保持DDS 原有优点的基础上,尽量减少硬件复杂性,降低电路的面积和功耗,提高芯片速度。综合以上考虑,所设计DDS 的系统结构框图如图1.2.2 所示:
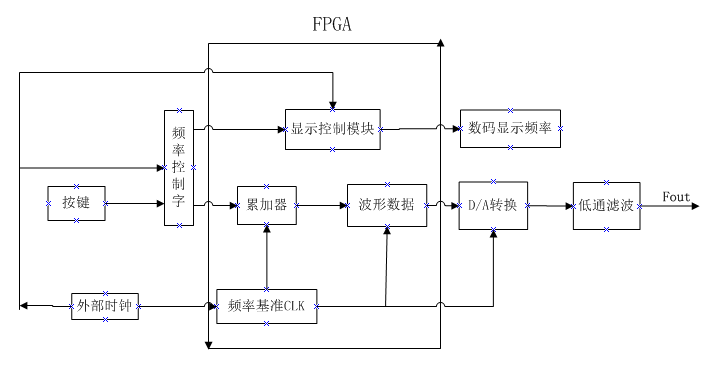
图1.2.2
取时钟频率为输出正弦波最高频率的4倍。即Fclk=4*Fmax=4*5120=20480Hz。由于使用的FPGA芯片的晶振频率为16.384MHz,所以需要对其进行分频操作,地址范围Ymax=Fclk/F=20480/80=256。因此对每个正弦波采样256点。假设波峰为FFH,波谷为00H,每个采样点的取值可由公式Y=128*Sin(2π*)+128算出。
2 单元电路设计
2.1 FPGA实验板
FPGA实验板上存储了256个采样值并输出给后级的DAC电路。同时通过2个按键和4位数码管实现频率字增减和显示。芯片使用ALTERA的EP1C6T144C8N。利用其丰富的I /O 资源, 并行处理数据。具有高密度、高速度、多功能、低功耗、设计灵活方便、可反复编程等特点。
2.2 DAC0832模块
DAC0832芯片以其价格低廉、接口简单、转换控制容易等优点,在嵌入式应用系统中得到广泛的应用。本设计中,DAC0832把FPGA实验板输出的8路数字信号转换成模拟信号,原理图如图2.2.1所示:
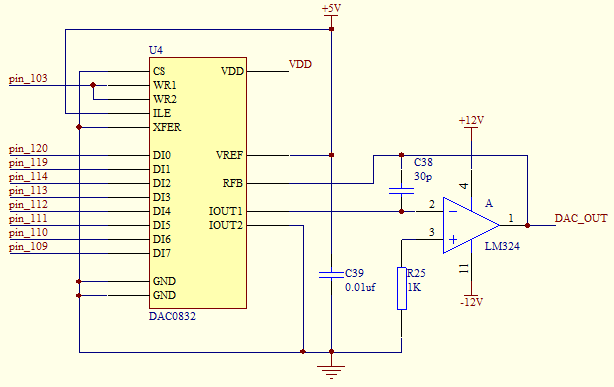
图2.2.1
D/A转换结果采用电流形式输出。若需要相应的模拟电压信号,可通过一个高输入阻抗的线性运算放大器实现。运放的反馈电阻可通过RFB端引用片内固有电阻,也可外接。
2.3三阶低通滤波器
DAC0832模块输出的信号含有高次谐波分量,需要用滤波器滤除。本设计采用三阶低通滤波器,该滤波器由一个二阶巴特沃斯低通滤波器和一个一阶无源RC低通滤波器组成。其原理图如图2.3.1所示:
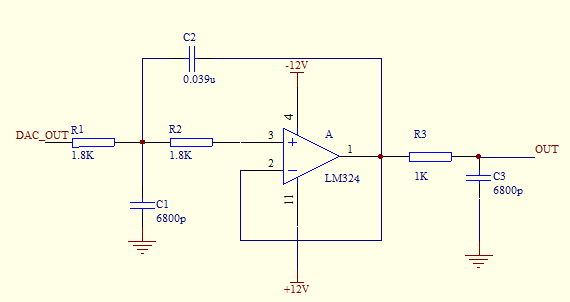
图2.3.1
取截止频率略高于一次谐波频率(5.4KHz),由公式Fc1=,Fc2=,计算得R1=R2=1.8K,C1=C3=6800p,C2=0.039u,R3=4.3K
3 软件设计
3.1软件工作流程图
软件工作流程图如图3.1.1所示
图 3.1.1
程序综合报告


4 系统调试
采用分模块调试的方法,先观察FPGA实验板上数码管是否正常显示,按键能否增减频率字,然后用示波器测是否有输出信号。再接上DAC0832模块,看DAC_OUT输出端是否输出阶梯形状的波形,如果波形有出入,则是程序的问题。
程序修改后。把DAC_OUT接到三阶低通滤波器输入端,看输出端是否为正弦波,若波形有棱角或顶部尖锐,说明滤波器对高次谐波分量的衰减还不够,改变滤波器中的元件参数,直到输出正确的正弦波。
观察示波器测得的波形,频率误差极小,波形无失真,满足课题要求。
总结
通过这个课题使我们掌握了DDS的工作原理以及优势。与传统正弦波振荡器相比,DDS的精度更高,抗干扰能力强,修改波形时无需重新设计电路,只要修改采样点的电压值即可。相对于基于PLL的频率合成器,DDS的结构更简单,设计周期更短。
由于所用FPGA的晶振频率远比输出波形高,可加大采样频率,使用更高位数的DAC芯片,进一步提高输出波形的频率分辨率。除此以外,若想要获得更多波形,可以输入其采样值,然后设计一个波形切换功能。也可以对输出的正弦波进行信号处理,获得其他的波形。
参考文献
[1] 薛文 DDS 任意波形发生器的设计与实现[D]。南京:南京理工大学,2004。22~31。
[2] 韩军功 基于DDS 的任意波形发生器的研制[D]。西安:西安电子科技大学,2002。
[3] 卢毅,赖杰 VHDL 与数字电路设计[M]。北京:科学出版社,2001。
附录
元器件清单
FPGA实验板 x1
芯片:LM324 x1, DAC0832 x1
电阻:1k x2, 1.8k x2
电容:30p x1, 6800pf x2, 0.01uf x1, 0.039uf x1