1. 引言

本文是"计算机图形和深度学习模型NeRF详解"系列文章的续篇，进一步深入探讨了NeRF的核心技术。NeRF作为一项突破性技术，因其能够从有限的2D图像中重建出完整的3D场景，而在多个领域，如医学成像、3D场景重建、动画、场景重照明和深度估计等，引起了极大的兴趣。

在前一部分，我们对NeRF的基础知识和所用数据集有了初步了解。本篇则专注于NeRF算法如何利用稀疏图像集合捕捉3D场景的详细实现过程。教程内容被合理划分为多个部分，涵盖了NeRF的介绍、数据输入流程、射线生成、采样点设置、多层感知器在NeRF中的应用、体积渲染技术、光度损失计算以及NeRF的高级特性，如位置编码和分层采样等，构建了一个全面而系统的学习路径。

本文的亮点在于，它不仅阐述了NeRF的理论基础，还通过代码示例和实践练习，帮助读者深刻理解并应用NeRF技术。通过深入阅读和练习，读者将能够掌握NeRF的工作机制和操作方法，为进一步的探索和应用打下坚实的基础。

此外，本文还提供了源代码的下载链接，方便读者在实践过程中进行参考。整体来看，这是一篇内容丰富、结构清晰、实用性强的教程，对于希望深入了解和学习NeRF技术的读者来说，是一份极具价值的资源。

2.NeRF模型

让我们探讨这篇论文的出发点。假设你手头有一组特定视角下的图像，它们捕捉了一个场景。你的目标是利用这些图像，从一个新的视角创造出该场景的图像。这涉及到新颖图像合成领域，就像图1所展示的那样。

图1：新视角的产生

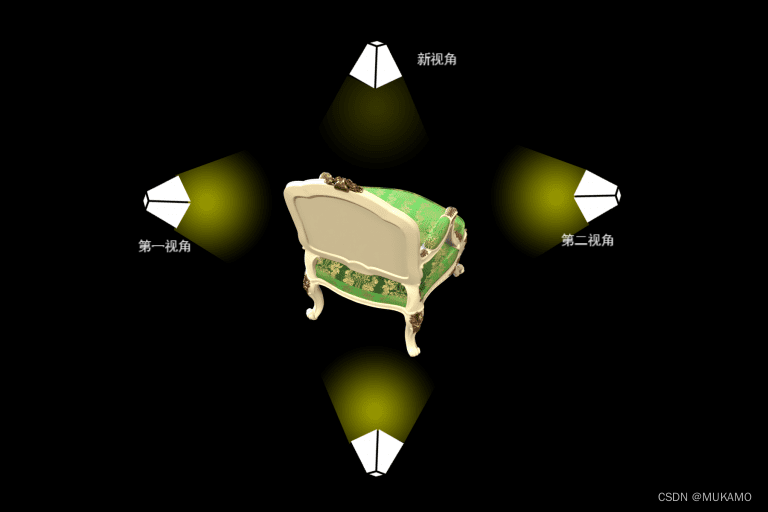
我们首先想到的新颖视角合成的解决方案可能是在训练数据集上使用生成对抗网络（GAN）。使用GAN，我们将自己限制在图像的二维空间内。

然而，Mildenhall等人（2020年）提出了一个简单的问题。

为什么不直接从图像中捕捉整个三维景观呢？

让我们花点时间来吸收这个想法。

我们现在面临的是一个转变后的问题陈述。从新颖视角合成，我们已经转向了从一组稀疏的二维图像中捕获三维场景。

这个新的问题陈述也将作为解决新颖视角合成问题的一种方法。如果我们手头有三维景观，生成一个新的视角有多困难呢？

请注意，NeRF并不是第一个解决这个问题的方法。它的前身使用了各种方法，包括卷积神经网络（CNN）和基于梯度的网格优化。然而，根据论文，这些方法由于空间和时间复杂度的增加，无法扩展到更高的分辨率。NeRF的目标是优化一个底层的连续体积场景函数。

如果你一开始没有完全理解这些术语，请不要担心。博客的其余部分致力于详细分解这些主题，并逐一解释它们。

我们从一组稀疏的图像及其对应的相机元数据（方向和位置）开始。接下来，我们希望实现整个场景的三维表示，如图2所示。

图2：3D场景图像（来源：改编自Mildenhall等人，2020年，第5页，图2）

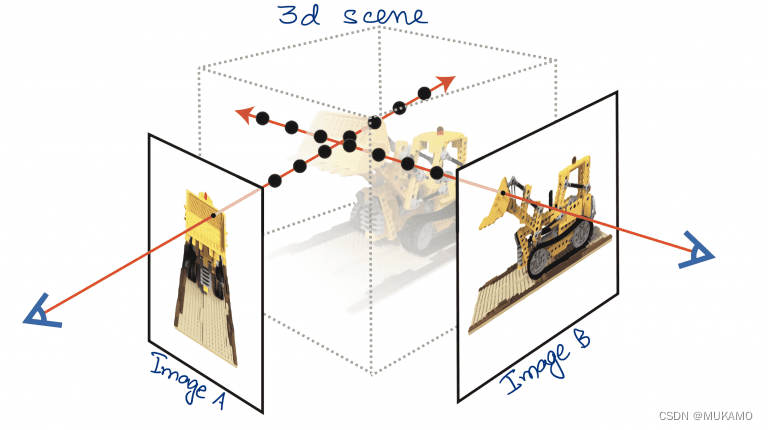
NeRF的步骤可以通过以下图表来可视化：

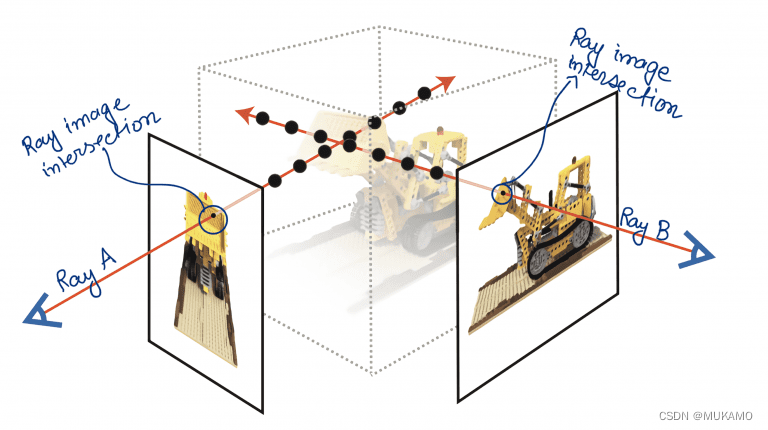
生成射线：在这个步骤中，我们通过图像的每个像素点发射射线。射线（射线A和射线B）是图中的红线（如图4所示），它们与图像相交并穿过三维盒子（场景）。翻译并改写如下：

在NeRF的流程中，我们首先进行的是射线生成阶段：这一阶段涉及从图像的每个像素点发射出射线。如图4中的红色线条所示，这些射线（例如射线A和射线B）与图像相交，并延伸穿过整个三维空间（场景）。

图3：光线穿过图像并穿越3D场景（来源：改编自Mildenhall等人，2020年，第5页，图2）

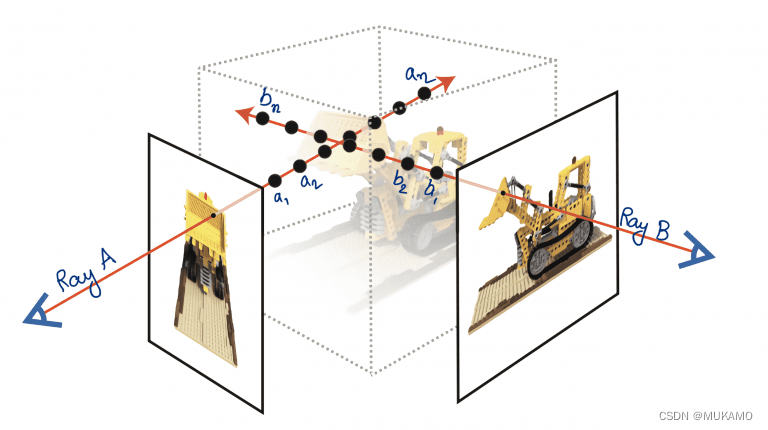
2.1.采样点

在NeRF的采样点阶段，我们沿着射线在图5中展示的位置选取一系列点，记为（$a_1,a_2,a_3,\dots ,a_n$）。这些点沿着射线分布，它们在三维空间中定位，位于场景的三维盒子内。

图4：从光线中采样点（来源：改编自Mildenhall等人，2020年，第5页，图2）

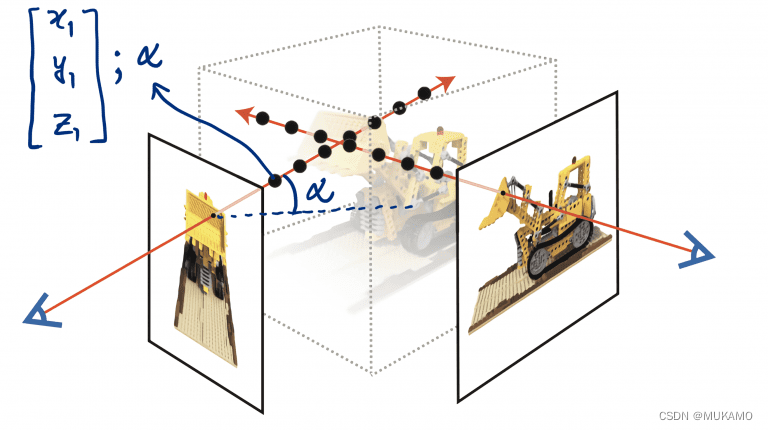
在图5中，我们可以看到每个采样点都具有一个特定的三维坐标位置（x, y, z），并且它们都具有一个方向分量（𝛼），这个方向分量与射线的走向紧密相连。这意味着每个点的方向性与其所处射线的指向是一致的。

图5：每个点的空间位置和方向（来源：改编自Mildenhall等人，2020年，第5页，图2）

2.2.深度学习

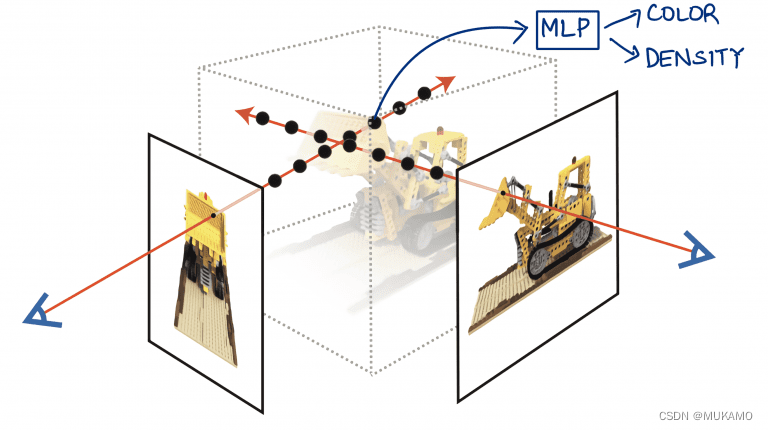
在深度学习阶段，我们把这些采样点送入一个多层感知器网络（如图6），以此来预测每个点的颜色和密度值。

图6：点送入多层感知机（MLP）中（来源：改编自Mildenhall等人，2020年，第5页，图2）

2.3.体积渲染

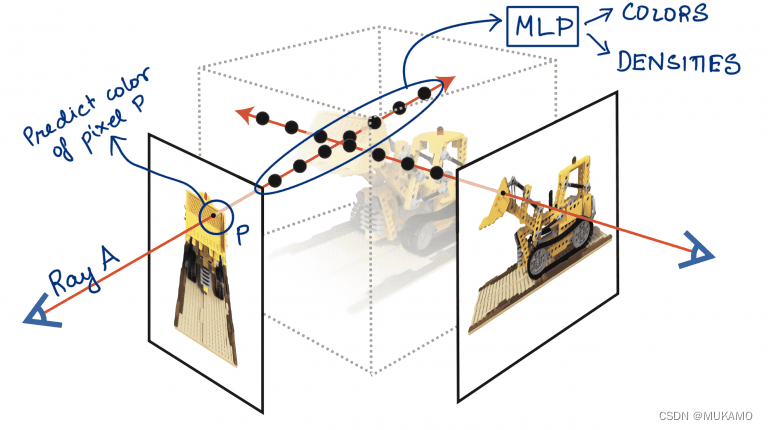
在体积渲染阶段，我们专注于一条特定的射线，比如射线A。我们将这条射线上的所有采样点数据输入到多层感知器中，以获取每个点的颜色和密度信息，这在图7中有所展示。一旦我们得到了这些点的颜色和密度，就可以利用传统的体积渲染方法（将在后续部分详细解释），来预测射线穿过的图像像素，即像素P的颜色。这种方法允许我们综合考虑沿射线的所有采样点信息，从而生成新视角下的图像像素颜色。

图7：体积渲染过程（来源：改编自Mildenhall等人，2020年，第5页，图2）

2.4.计算光度损失

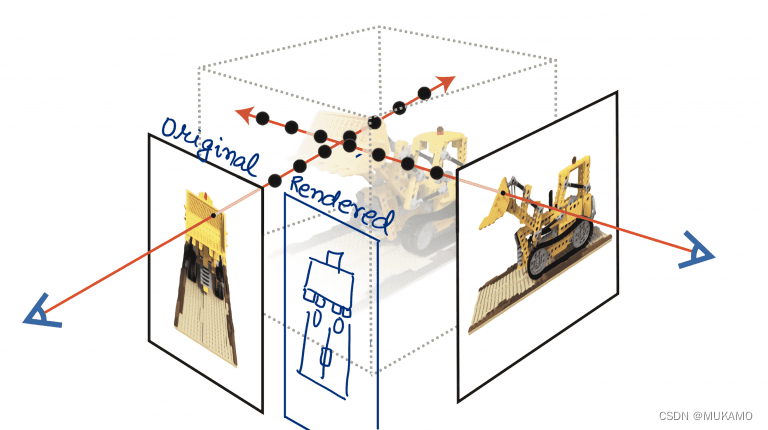
在光度损失计算中，我们比较预测的像素颜色与实际观察到的像素颜色之间的差异，这种差异被定义为光度损失。如图8所示，通过评估这种差异，我们可以对多层感知器网络进行反向传播操作，目的是为了减少预测误差，优化网络参数，从而最小化整体的光度损失。这个过程是深度学习中常见的优化手段，有助于提高模型的预测准确性。

图8：计算光度损失（来源：改编自Mildenhall等人，2020年，第5页，图2）

3.数据输入管道

现在，我们对NeRF有了一个高层次的认识。但在深入讨论算法之前，我们需要先构建一个输入数据的流程。

根据之前的教程，我们知道我们的数据集中包含了图像及其对应的相机方向信息。因此，我们现在需要创建一个能够产生图像和相应射线的数据管道。

在本节中，我们将利用tf.data API逐步构建这个数据管道。tf.data是一个确保数据集高效构建和使用的API。如果你需要关于tf.data的入门知识，可以参考相关教程。

3.1. 设置

# import the necessary packages
from tensorflow.io import read_file
from tensorflow.image import decode_jpeg
from tensorflow.image import convert_image_dtype
from tensorflow.image import resize
from tensorflow import reshape
import tensorflow as tf
import json

3.2.数据导入

def read_json(jsonPath):
    # 打开json文件
    with open(jsonPath, "r") as fp:
        # 读取json数据
        data = json.load(fp)
    
    # 返回数据
    return data

首先，我们在代码的第2至8行导入了构建数据管道所需的必要库：

• tensorflow用于数据管道的构建
• json用于读取和操作JSON格式的数据

接着，我们在第10至17行定义了一个名为read_json的函数，它接受指向JSON文件的路径（jsonPath）并解析该文件，返回解析后的数据结构。

在第12行，我们调用open函数以读取模式打开指定的JSON文件。获取文件对象后，在第14行利用json.load函数来读取并解析JSON数据。解析完成后，第17行将解析得到的数据作为返回值输出。

def get_image_c2w(jsonData, datasetPath):  
    # 定义一个列表来存储图像路径  
    imagePaths = []  
      
    # 定义一个列表来存储相机到世界矩阵（camera-to-world matrices）  
    c2ws = []  
  
    # 遍历数据中的每一帧  
    for frame in jsonData["frames"]:  
        # 获取图像文件名  
        image_file_name = frame["file_path"]  
        # 替换文件名中的相对路径为完整的数据集路径  
        # 注意：这里假设json中的file_path是相对路径，并需要将其替换为完整的绝对路径  
        # 这里使用字符串替换方法可能不太准确，应该根据具体文件结构来决定如何构建完整路径  
        # 例如，如果file_path是"images/0001.jpg"，则可能需要拼接datasetPath和file_path  
        # 这里假设datasetPath已经是包含"images"文件夹的完整路径  
        # imagePath = os.path.join(datasetPath, image_file_name)  
        # 考虑到注释中直接进行了字符串替换，这里我们暂时保持这种简单替换方式  
        # 但是需要注意，如果数据集路径中有多个部分或者存在目录层级，则需要使用正确的路径拼接方式  
        # 这里仅作为示例，假设datasetPath是一个文件夹路径，不包含文件名中的"images"部分  
        imagePath = image_file_name.replace(".", datasetPath)  # 注意：这里可能不是正确的路径拼接方式  
        # 添加完整的图像路径（包括文件扩展名）到列表中  
        imagePaths.append(f"{imagePath}.png")  # 这里假设所有图像都是png格式，并且json中未提供扩展名  
  
        # 获取相机到世界矩阵  
        c2w = frame["transform_matrix"]  # 注意：这里将变量名从c2ws更改为c2w，因为每次迭代只需要一个矩阵  
        c2ws.append(c2w)  
      
    # 返回图像文件名列表和相机到世界矩阵列表  
    return (imagePaths, c2ws)

这段代码定义了一个名为 get_image_c2w 的函数，其作用是从 JSON 数据和数据集路径中提取图像路径和相应的相机到世界矩阵。以下是代码的功能描述：

1. 定义函数：get_image_c2w 函数接收两个参数，jsonData（包含数据帧的 JSON 对象）和 datasetPath（数据集的路径）。

2. 初始化列表：

   • imagePaths：用于存储图像的完整路径。
   • c2ws：用于存储每帧的相机到世界矩阵。

3. 遍历数据帧：使用 for 循环遍历 jsonData 中的 “frames” 列表，每一项代表一帧数据。

4. 处理图像路径：

   • 从每帧数据中获取 image_file_name。
   • 将相对路径替换为完整的数据集路径。这里假设 image_file_name 是相对于数据集路径的相对路径，并将其替换为绝对路径。注意，这里的替换方法可能需要根据实际的文件结构进行调整。
   • 将处理后的图像路径添加到 imagePaths 列表中，并假设所有图像格式为 png。

5. 处理相机到世界矩阵：

   • 从每帧数据中获取 transform_matrix，即相机到世界的变换矩阵。
   • 将矩阵添加到 c2ws 列表中。

6. 返回结果：函数返回一个包含图像路径列表和相机到世界矩阵列表的元组。

代码中的一些注意点：

• 路径拼接方法可能需要根据实际的文件系统结构进行调整，以确保正确地构建图像的完整路径。
• 假设 JSON 数据中的 file_path 是相对于某个 “images” 目录的路径，而 datasetPath 已经包含了这个目录的完整路径。
• 函数中的变量名 c2w 用于表示单个矩阵，而 c2ws 用于表示存储所有矩阵的列表。
• 代码中的注释强调了在实际应用中可能需要更精确的文件路径处理方法，而不仅仅是简单的字符串替换。

这个函数是数据处理流程的一部分，通常用于准备训练数据，将 JSON 格式的元数据转换为可用于机器学习模型的格式。

为了在使用tf.data.Dataset对象时对数据集进行必要的转换以供模型使用，我们采用了map方法。这个方法接收一个tf.data.Dataset对象和一个将要应用于数据集中每个元素的函数。

后续部分，定义了一些函数，这些函数与map方法结合使用，目的是对数据集中的数据进行适当的转换处理。

import tensorflow as tf  
  
class GetImages():  
    def __init__(self, imageWidth, imageHeight):  
        # 定义图像的宽度和高度  
        self.imageWidth = imageWidth  
        self.imageHeight = imageHeight  
  
    def __call__(self, imagePath):  
        # 读取图像文件  
        image_string = tf.io.read_file(imagePath)  
  
        # 解码JPEG图像字符串  
        image = tf.image.decode_jpeg(image_string, channels=3)  
  
        # 将图像数据类型从uint8转换为float32  
        image = tf.image.convert_image_dtype(image, tf.float32)  
  
        # 调整图像大小到配置中的高度和宽度  
        image = tf.image.resize(image, [self.imageHeight, self.imageWidth])  
  
        # 不需要reshape，因为resize已经返回了正确形状的Tensor  
  
        # 返回图像  
        return image  
  
# 使用示例  
get_images = GetImages(imageWidth=256, imageHeight=256)  
image = get_images('path/to/your/image.jpg')

在我们深入下一步之前，让我们解释一下为什么我们决定创建一个包含__call__方法的类，而不是简单地创建一个能够用map函数应用的函数。

原因在于，传递给map的函数只能接受数据集中的单个元素，这是一个限制条件，我们需要找到方法来绕过它。

为了解决这个问题，我们设计了一个类，该类可以包含一些属性（例如imageWidth和imageHeight），这些属性将在函数调用时使用。

这段代码定义了一个名为 GetImages 的类，它用于处理图像读取和预处理的步骤。以下是代码的功能描述：

1. 导入TensorFlow：首先，代码导入TensorFlow库。

2. 定义 GetImages 类：

   • 类初始化函数 __init__ 接收图像的宽度和高度作为参数，并保存这些值以供后续使用。

3. 定义 __call__ 方法：

   • 这个方法接收一个图像路径 imagePath 作为参数。
   • 使用 tf.io.read_file 读取图像文件的字符串。
   • 使用 tf.image.decode_jpeg 解码JPEG图像字符串，指定 channels=3 来确保图像是三通道的。
   • 使用 tf.image.convert_image_dtype 将图像的数据类型从 uint8 转换为 float32，这通常是为了后续处理（如归一化）的需要。
   • 使用 tf.image.resize 调整图像大小到指定的 imageHeight 和 imageWidth。

4. 返回处理后的图像：处理后的图像通过 return 语句返回。

5. 使用示例：

   • 创建 GetImages 类的实例 get_images，指定图像的宽度和高度为256像素。
   • 调用 get_images 实例，传入图像路径 'path/to/your/image.jpg'，这将触发 __call__ 方法并返回处理后的图像。

这个类的设计模式允许它的行为类似于函数，通过 __call__ 方法可以直接调用类的实例，这在处理图像数据时提供了一种方便和灵活的方式。通过这种方式，可以轻松地将图像读取和预处理集成到数据管道中。

3.3.生成射线

在计算机图形学领域，光线的路径可以通过一个参数化公式来表示：

$$\vec{r}(t)=\vec{o}+t\vec{d}$$

在这个公式中：

• $\vec{r}(t)$表示光线在参数 (t) 处的位置。
• $\vec{o}$是光线的起始点，即原点。
• $\vec{d}$是表示光线方向的单位向量。
• t是一个参数，可以视为时间或其他连续变量。

在NeRF的实现中，我们创建光线是通过将图像平面上的像素点作为光线的原点，并且将通过该像素点到达相机光圈的直线定义为光线的方向。这一过程在图9中有详细的图示说明。

图9：射线生成过程

我们能够利用简单的方程式来确定相机坐标系下二维图像中每个像素的具体位置。
$$u=f\frac{x_c}{z_c}+o_x\Rightarrow x_c=z_c\frac{u-o_x}{f}$$
$$v=f\frac{y_c}{z_c}+o_y\Rightarrow y_c=z_c\frac{v-o_y}{f}$$
在前面的内容中，我们已经掌握了如何轻松确定像素点作为原点的位置，但要获取光线的方向则涉及到一些更复杂的问题。
$${\tilde{x}}_c=C_{ex}\times {\tilde{X}}_w\Rightarrow {\tilde{X}}_w={C_{ex}}^{-1}\times {\tilde{X}}_c$$

我们需要的相机到世界坐标系的转换矩阵，即逆矩阵$C_{ex}^{-1}$，可以直接从数据集中提取得到。
$${C_{ex}}^{-1}=\left[\begin{array}{cccc}{r}_{11}^{\prime }& r_{12}^{\prime }& r_{13}^{\prime }& t_x^{\prime }\\ r_{21}^{\prime }& r_{22}^{\prime }& r_{23}^{\prime }& t_y^{\prime }\\ r_{31}^{\prime }& r_{32}^{\prime }& r_{33}^{\prime }& t_z^{\prime }\\ 0& 0& 0& 1\end{array}\right]$$
在定义光线的方向向量时，我们并不需要整个从相机到世界坐标系的矩阵。我们真正需要的是矩阵的上半部分，即3x3的旋转矩阵，它负责定义相机的朝向。
$$R_{ex}^{\prime }=\left[\begin{array}{ccc}{r}_{11}^{\prime }& r_{12}^{\prime }& r_{13}^{\prime }\\ r_{21}^{\prime }& r_{22}^{\prime }& r_{23}^{\prime }\\ r_{31}^{\prime }& r_{32}^{\prime }& r_{33}^{\prime }\end{array}\right]$$
有了旋转矩阵，我们可以通过以下方程来计算单位方向向量：
$$\vec{d}=\frac{R_{ex}^{\prime }\times X_c}{|R_{ex}^{\prime }\times X_c|}$$
困难的计算部分已经结束。接下来是简单的部分，我们将使用相机到世界矩阵中的平移向量作为光线的起始点。
$$t_{ex}^{\prime }=\left[\begin{array}{c}{t}_x^{\prime }\\ t_y^{\prime }\\ t_z^{\prime }\end{array}\right]$$
让我们看看如何将这个转换为代码。我们将继续使用pyimagesearch/data.py文件。

在Python中，如果你有一个旋转矩阵（通常是3x3的矩阵），并且你想要从这个矩阵中提取单位方向向量，你可以这样做。但是，需要注意的是，旋转矩阵本身并不直接表示一个单位方向向量，而是表示一个坐标系相对于另一个坐标系的旋转。然而，如果你知道旋转矩阵是如何构建的（例如，它可能从某个方向向量开始），那么你可以从该矩阵中提取信息。

class GetRays:  
    def __init__(self, focalLength, imageWidth, imageHeight, near, far, nC):  
        # 定义焦距、图像宽度和图像高度  
        self.focalLength = focalLength  
        self.imageWidth = imageWidth  
        self.imageHeight = imageHeight  
  
        # 定义近点和远点的边界值  
        self.near = near  
        self.far = far  
  
        # 定义粗模型中的样本数量  
        self.nC = nC  
  
    # 这里可以添加其他方法来生成光线，例如根据像素位置和相机参数计算光线的原点和方向  
  
    # 示例方法：计算给定像素位置的光线的原点和方向  
    def get_ray(self, pixel_x, pixel_y):  
        # 根据相机参数和像素位置计算光线的原点和方向（这里仅展示伪代码）  
        # 假设图像平面位于相机坐标系中z=focalLength的位置  
        # 原点（o）通常位于图像平面的中心，并可以通过像素位置进行调整  
        # 方向（d）是连接相机中心和像素点的单位向量  
  
        # 计算原点（这里仅给出示例公式，实际计算可能更复杂）  
        # origin = ...  
  
        # 计算方向（这里仅给出示例公式，实际计算可能更复杂）  
        # direction = ...  
  
        # 返回光线的原点和方向  
        return origin, direction  
  
# 使用示例  
# 假设我们有一个相机对象，并知道其参数  
rays_obj = GetRays(focalLength=50, imageWidth=640, imageHeight=480, near=0.1, far=10.0, nC=64)  
  
# 我们可以使用上述的get_ray方法来获取某个像素位置的光线  
# 注意：get_ray方法在这里是伪代码，你需要根据实际的相机模型和图像平面位置来实现它  
# ray_origin, ray_direction = rays_obj.get_ray(pixel_x=320, pixel_y=240)

这段代码是一个类的 __call__ 方法，它根据相机到世界的变换矩阵计算图像中每个像素对应的世界空间中的射线。以下是代码的功能描述：

1. 创建图像尺寸网格：使用 tf.meshgrid 函数创建图像宽度和高度的网格，用于后续计算每个像素对应的射线。

2. 定义相机坐标系中的坐标：计算图像平面上每个像素点的相机坐标系坐标 (xCamera, yCamera)。这里假设图像的中心是原点，焦距是图像宽度或高度的一半，这可能需要根据实际相机参数进行调整。

3. 定义相机向量：将 xCamera 和 yCamera 与 -1 组合，形成指向图像平面负 z 方向的相机向量 xCyCzC。这里 yCamera 前加了负号，以匹配可能与图像坐标系相反的相机坐标系 y 轴。

4. 从 camera2world 矩阵中提取旋转和平移信息：

   • rotation：从 camera2world 矩阵中提取的3x3旋转矩阵，用于将相机坐标转换为世界坐标。
   • translation：从 camera2world 矩阵中提取的平移向量，表示相机在世界坐标系中的位置。

5. 射线计算说明：注释中提到，此 __call__ 方法只计算了部分射线信息。完整的射线信息，包括射线的原点和方向，通常需要进一步的计算才能得到。

这个方法是3D场景理解和渲染流程的一部分，它将相机坐标系下的像素坐标转换为对应的世界空间射线，这些射线对于体积渲染和3D场景重建至关重要。通过这种方法，可以从2D图像数据中推断出3D场景的结构。

def __call__(self, camera2world):  
    """  
    根据相机到世界的变换矩阵，计算图像中每个像素对应的世界空间中的射线  
  
    参数:  
        camera2world: 相机到世界的变换矩阵，形状为 (4, 4)  
  
    返回:  
        无返回值，但会计算图像像素对应的世界空间射线，通常用于后续渲染等步骤  
    """  
    # 创建图像尺寸的网格  
    (x, y) = tf.meshgrid(  
        tf.range(self.imageWidth, dtype=tf.float32),  
        tf.range(self.imageHeight, dtype=tf.float32),  
        indexing="xy",  
    )  
  
    # 定义相机坐标系中的坐标  
    # 这里的计算假设图像中心是原点，焦距为图像宽度/高度的一半（需要根据实际情况调整）  
    xCamera = (x - self.imageWidth * 0.5) / self.focalLength  
    yCamera = (y - self.imageHeight * 0.5) / self.focalLength  
  
    # 定义相机向量，从相机出发指向图像平面的负z方向  
    # 注意，yCamera前面加上了负号，因为图像坐标系和相机坐标系y轴方向可能相反  
    xCyCzC = tf.stack([xCamera, -yCamera, -tf.ones_like(x)], axis=-1)  
  
    # 从camera2world矩阵中切片得到旋转矩阵和平移向量  
    # 旋转矩阵是camera2world的前3行前3列  
    rotation = camera2world[:3, :3]  
    # 平移向量是camera2world的前3行最后一列  
    translation = camera2world[:3, -1]  
  
    # 注意：此函数仅计算了部分信息，完整的射线信息（如原点和方向）通常还需要进一步计算

__call__: 当我们调用这个方法时，需要传入一个相机到世界的矩阵。这个方法会计算并返回：

• rayO: 表示光线起始点的集合。
• rayD: 表示光线方向的向量集合。
• tVals: 沿光线采样的点的集合。

在代码的第79至83行，我们根据图像的尺寸创建了一个网格，这个网格对应于我们在图10中看到的图像平面。

随后，在第86和87行，我们利用之前推导出的公式来计算得到每个像素点在相机坐标系中的位置。
$$u=f\frac{x_c}{z_c}+o_x\Rightarrow x_c=z_c\frac{u-o_x}{f}$$
$$v=f\frac{y_c}{z_c}+o_y\Rightarrow y_c=z_c\frac{v-o_y}{f}$$
在代码的第90和91行，我们创建了一个齐次坐标表示，将相机坐标 $(x_C,y_C,z_C)$ 堆叠起来形成向量 $x_C{y}_C{z}_C$。

接着，在第95和96行，我们从相机到世界的矩阵中分解出旋转矩阵和相机的平移向量，以便用于后续的光线追踪计算。

import tensorflow as tf  
  
# 假设 xCyCzC 是相机坐标系下的坐标，rotation 是从相机坐标系到世界坐标系的旋转矩阵  
# translation 是从相机坐标系到世界坐标系的平移向量  
  
# 扩展相机坐标以添加一个批次维度（假设 xCyCzC 的形状是 [H, W, 3]）  
# 将相机坐标扩展为 [H, W, 1, 3]  
xCyCzC = xCyCzC[..., None, :]  
  
# 获取世界坐标系下的坐标  
# 将相机坐标通过旋转矩阵变换到世界坐标系  
xWyWzW = xCyCzC * rotation  
  
# 计算射线的方向向量  
# 对 xWyWzW 进行求和（沿着最后一个维度），得到方向向量的原始长度  
rayD = tf.reduce_sum(xWyWzW, axis=-1, keepdims=True)  
# 对方向向量进行归一化，得到单位方向向量  
rayD = rayD / tf.norm(rayD, axis=-1, keepdims=True)  
  
# 计算射线的原点向量  
# 将平移向量 broadcast 到与 rayD 相同的形状  
# 注意：如果 TensorFlow 版本较旧，可能需要使用 tf.tile 替代 tf.broadcast_to  
rayO = tf.broadcast_to(translation, tf.shape(rayD))  
  
# 从射线中获取样本点  
# 生成从 near 到 far 的等距值作为 t 值  
tVals = tf.linspace(self.near, self.far, self.nC)  
# 根据 rayO 的形状确定噪声的形状，并生成随机噪声  
noiseShape = list(rayO.shape[:-1]) + [self.nC]  
noise = (tf.random.uniform(shape=noiseShape) *   
         (self.far - self.near) / self.nC)  
# 将噪声添加到 t 值中  
tVals = tVals + noise  
  
# 返回射线的原点、方向和样本点  
# 注意：可能需要调整 tVals 的形状，以匹配 rayO 和 rayD 的形状  
# 这里假设 rayO 和 rayD 的形状是 [H, W, 1, 3]，则 tVals 也应该是 [H, W, 1, nC]  
tVals = tf.expand_dims(tVals, axis=-2)  # 确保 tVals 与 rayO 和 rayD 维度匹配  
return (rayO, rayD, tVals)

这段代码是一个用于生成射线及其样本点的过程，这些射线用于3D场景的体积渲染。以下是代码的功能描述：

1. 导入TensorFlow：首先，代码导入TensorFlow库。

2. 扩展相机坐标：xCyCzC 是一个形状为 [H, W, 3] 的张量，表示相机坐标系下的坐标点。代码通过添加一个新的维度，将其扩展为 [H, W, 1, 3]，为后续的批处理操作做准备。

3. 获取世界坐标：使用旋转矩阵 rotation 将相机坐标 xCyCzC 转换到世界坐标系 xWyWzW。

4. 计算射线方向向量：通过对 xWyWzW 沿最后一个维度求和并归一化，得到射线的方向向量 rayD。

5. 计算射线原点向量：使用 translation 作为平移向量，将其扩展（broadcast）到与 rayD 相同的形状 rayO，作为射线的原点。

6. 生成样本点：代码使用 tf.linspace 生成从近平面 self.near 到远平面 self.far 的等间距 t 值，这些 t 值用于定义射线上的样本点。

7. 添加噪声：为增加样本点的随机性，代码生成与 tVals 形状相同的随机噪声，并将其添加到 tVals 中。

8. 调整样本点形状：确保 tVals 的形状与 rayO 和 rayD 匹配，以便可以用于后续的体积渲染计算。

9. 返回结果：函数返回射线的原点 rayO、方向 rayD 以及样本点 tVals。

这个过程是NeRF算法的一部分，用于设置从相机出发穿过3D场景的射线，并在这些射线上定义一系列的样本点，这些点将被用于估计场景的颜色和密度。通过这种方式，可以从一组稀疏的2D图像中重建出3D场景。

3.4.采样

完成光线生成之后，接下来的步骤是从这些光线中提取样本化的三维空间点。我们有两种建议的方法来实现这一过程。

均匀间隔采样点：这个方法顾名思义，就是按照均匀的间隔在光线上进行点的采样，这种采样方式在图10中有所展示。

图10：固定间隔采样
采样公式如下：
$$t_i=i\frac{t_f-t_n}{N}$$

光线上的$t_f$和$t_n$分别表示最远和最近的采样点。我们将光线均匀划分为( N )个间隔相等的部分，每个划分点即为采样点。

随机采样点：这种方法中，我们在采样过程中加入了随机性。通过从光线上的随机位置采样点，可以使模型接触到更多样化的数据，这有助于提高模型的泛化能力，从而获得更佳的输出效果。这种采样策略在图12中有详细说明。

图11：随机采样

随机采样公式如下：
$$t_i=U[t_n\frac{i-1}{N}(t_f-t_n),t_n+\frac{i}{N}(t_f=t_n)]$$
在这种方法中，我们采用均匀采样的方式，即在两个连续采样点之间的区域随机选择一个点作为新的采样点。

4.建立模型

4.1.构建NeRF层

采样点的每个实例都具有五个维度。它们的空间位置由一个三维向量（x, y, z）定义，而方向则由一个二维向量（$\theta ,\varphi$）定义。Mildenhall等人（2020年）建议使用3D笛卡尔坐标系下的单位向量 $d$来表达观察方向。

这些五维的采样点输入到多层感知器（MLP）中。在论文中，由这些带有五维采样点的光线构成的场被称为神经辐射场。

MLP网络的任务是预测每个输入采样点的颜色$c$和体积密度$\sigma$。其中，颜色指的是该点的红（r）、绿（g）、蓝（b）颜色值。体积密度可以理解为光线在该点处遇到一个无限小粒子的概率密度。

MLP的具体网络结构在图12中有所展示。

图12：MLP（多层感知机）架构

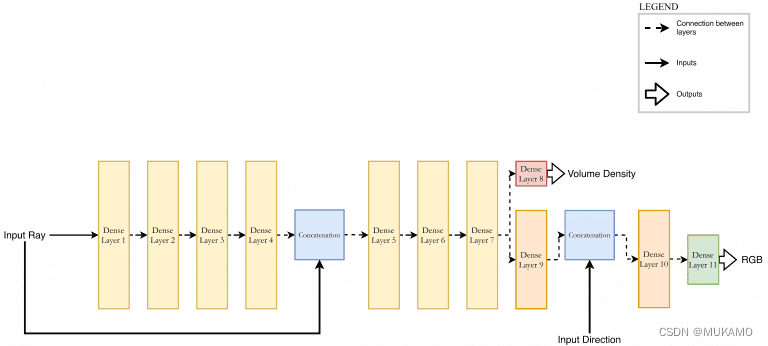
特别需要指出的是：

为了实现多视角的一致性表示，网络被设计为仅基于位置向量 $x$来预测体积密度 $\sigma$，而对于RGB颜色$c$的预测，则同时考虑了位置和观察方向。

在掌握了这些理论知识之后，我们可以开始着手在TensorFlow中实现NeRF的架构。接下来，我们将打开 pyimagesearch/nerf.py 文件，进一步深入了解其实现细节。

# 导入必要的包  
# Dense：用于添加全连接层  
# concatenate：用于合并多个张量（通常是特征向量）  
# Input：用于实例化输入张量  
# Model：用于实例化模型  
  
from tensorflow.keras.layers import Dense  
from tensorflow.keras.layers import concatenate  
from tensorflow.keras import Input  
from tensorflow.keras.models import Model  # 修正：这里应该明确地从 keras.models 导入 Model  

from tensorflow.keras.layers import Input, Dense, concatenate  
from tensorflow.keras.models import Model  
  
def get_model(lxyz, lDir, batchSize, denseUnits, skipLayer):  
    # 构建射线的输入层  
    # shape中的None表示可以处理任意长度的射线，2 * 3 * lxyz + 3 是每个射线样本的维度  
    rayInput = Input(shape=(None, None, None, 2 * 3 * lxyz + 3),  
                     batch_size=batchSize, name='ray_input')  # 添加name属性以便后续引用  
  
    # 构建射线方向的输入层  
    # 2 * 3 * lDir + 3 是每个射线方向样本的维度  
    dirInput = Input(shape=(None, None, None, 2 * 3 * lDir + 3),  
                     batch_size=batchSize, name='dir_input')  # 添加name属性以便后续引用  
  
    # 创建MLP的输入  
    x = rayInput  
  
    # 循环构建全连接层  
    for i in range(8):  
        # 构建一个全连接层  
        x = Dense(units=denseUnits, activation="relu", name=f'dense_{i}')(x)  
  
        # 检查是否需要包含残差连接  
        if i % skipLayer == 0 and i > 0:  
            # 注入残差连接  
            x = concatenate([x, rayInput], axis=-1, name=f'residual_{i}')  
  
    # 获取sigma值  
    sigma = Dense(units=1, activation="relu", name='sigma')(x)  
  
    # 创建特征向量  
    feature = Dense(units=denseUnits, name='feature')(x)  
  
    # 将特征向量与方向输入合并，并通过一个全连接层  
    feature = concatenate([feature, dirInput], axis=-1, name='feature_dir_concat')  
    x = Dense(units=denseUnits//2, activation="relu", name='dense_after_concat')(feature)  
  
    # 获取rgb值  
    rgb = Dense(units=3, activation="sigmoid", name='rgb')(x)  
  
    # 创建NeRF模型  
    nerfModel = Model(inputs=[rayInput, dirInput],  
                      outputs=[rgb, sigma],  
                      name='nerf_model')  # 添加name属性以便后续引用  
  
    # 返回NeRF模型  
    return nerfModel

这段代码定义了一个函数 get_model，用于构建用于Neural Radiance Fields（NeRF）的多层感知器（MLP）模型。以下是代码的功能描述：

1. 导入必要的Keras层和模型：从tensorflow.keras.layers导入Input, Dense, concatenate，从tensorflow.keras.models导入Model。

2. 函数定义：get_model函数接受以下参数：

   • lxyz：用于xyz坐标位置编码的维度数。
   • lDir：用于方向向量位置编码的维度数。
   • batchSize：数据的批量大小。
   • denseUnits：MLP中每个全连接层的单元数。
   • skipLayer：设置残差连接的层间隔。

3. 构建输入层：

   • rayInput：射线的输入层，其形状由外部参数决定，包含批次大小和射线样本的维度。
   • dirInput：射线方向的输入层，同样包含批次大小和方向样本的维度。

4. 构建MLP：

   • 使用for循环创建多个全连接层（Dense），每层使用ReLU激活函数。
   • 根据skipLayer参数，每间隔一定层数就添加一次残差连接，增强模型的学习能力。

5. 计算体积密度：通过一个全连接层计算并获取体积密度sigma。

6. 创建特征向量：通过一个全连接层创建特征向量。

7. 合并特征向量和方向输入：将特征向量与射线方向输入dirInput合并。

8. 进一步处理合并后的特征：通过另一个全连接层进一步处理合并后的特征。

9. 计算RGB值：最后通过一个全连接层计算RGB值，使用Sigmoid激活函数将值压缩到0-1范围内。

10. 创建NeRF模型：使用Model类创建NeRF模型，将输入层和输出层（RGB和sigma）结合起来。

11. 返回模型：返回构建好的NeRF模型。

此函数是NeRF实现的核心，负责构建用于预测给定射线和方向的颜色和体积密度的神经网络模型。通过这种方法，可以从稀疏的2D图像中合成新的3D视图。

4.2.体积渲染

在本节中，我们探讨了如何执行体积渲染技术。我们利用多层感知器（MLP）预测出的颜色和体积密度来绘制三维场景。

将网络的预测结果应用到传统的体积渲染公式中，以此来确定一个特定点的颜色。例如，下面的公式就是用来实现这一目的的：

$$C(r)={\int }_{t_n}^{t_f}T(t)\sigma (r(t))c(r(t),d)dt$$

这看起来可能有点复杂，让我们将这个公式拆解成几个简单的部分。

• $C(r)$代表物体某点的颜色。

• $r(t)=o+td$ 代表射入网络的光线，其中各个变量的含义如下：

  • -$o$ 表示光线的起点。
  • -$d$表示光线的方向。
  • $t$表示近点和远点之间用于积分的均匀采样集合。

• $\sigma (r(t))$是体积密度，也可以理解为光线在点 ( t ) 处结束的微分概率。

• $c(r(t))$是光线在点 ( t ) 处的颜色。

这些构成了公式的基础部分。除此之外，还有一个额外的项 $T(t)$：
$T(t)=\exp \left(-{\int }_{t_n}^t\sigma (r(s))ds\right)$
这表示从近点$t_n$到当前点$t$ 沿光线的透射率。可以将其视为衡量光线穿透3D空间到某点的能力的指标。

现在，当我们将所有项结合在一起时，我们就能够完全理解这个公式了。

$C(r)={\int }_{t_n}^{t_f}T(t)\sigma (r(t))c(r(t),d)dt$

在3D空间中，物体的颜色被定义为在视平面的近点$t_n$和远点$t_f$之间对所有点 $t$进行采样时，透射率$T(t)$、体积密度$\sigma (r(t))$、当前点的颜色 $c(r(t))$ 以及光线方向 $d$的积分之和。

接下来，让我们看看如何在代码中表达这个过程。首先，我们将查看 pyimagesearch/utils.py 文件中的 render_image_depth 函数。

import tensorflow as tf  
  
# 假设 BATCH_SIZE, IMAGE_HEIGHT, IMAGE_WIDTH 已经在外部定义  
# 这些变量表示批次大小、图像高度和图像宽度  
  
def render_image_depth(rgb, sigma, tVals):  
    """  
    根据RGB颜色值、sigma值和tVals值渲染图像和深度图  
  
    Args:  
        rgb (Tensor): RGB颜色值，形状为 [BATCH_SIZE, IMAGE_HEIGHT, IMAGE_WIDTH, 3]  
        sigma (Tensor): sigma值，形状为 [BATCH_SIZE, IMAGE_HEIGHT, IMAGE_WIDTH, num_samples]  
        tVals (Tensor): t值（射线上的点），形状为 [BATCH_SIZE, IMAGE_HEIGHT, IMAGE_WIDTH, num_samples+1]  
  
    Returns:  
        tuple: 包含三个元素的元组，分别是渲染后的图像、深度图和权重  
  
    """  
    # 压缩sigma的最后一个维度  
    sigma = sigma[..., 0]  # 形状变为 [BATCH_SIZE, IMAGE_HEIGHT, IMAGE_WIDTH]  
  
    # 计算相邻tVals之间的差值  
    delta = tVals[..., 1:] - tVals[..., :-1]  # 形状变为 [BATCH_SIZE, IMAGE_HEIGHT, IMAGE_WIDTH, num_samples-1]  
  
    # 创建一个与delta相同形状的tensor，但最后一个维度为1，并填充最后一个维度为1e10  
    # 用于确保最后一个tVals点后的alpha为0  
    deltaShape = [tf.shape(rgb)[0], IMAGE_HEIGHT, IMAGE_WIDTH, 1]  # 使用tf.shape(rgb)[0]代替硬编码的BATCH_SIZE  
    delta = tf.concat(  
        [delta, tf.fill(deltaShape, 1e10)], axis=-1  
    )  # 形状变为 [BATCH_SIZE, IMAGE_HEIGHT, IMAGE_WIDTH, num_samples]  
  
    # 从sigma和delta值计算alpha  
    alpha = 1.0 - tf.exp(-sigma * delta)  
  
    # 计算指数项，以便更容易地进行后续计算  
    expTerm = 1.0 - alpha  
    epsilon = 1e-10  # 防止log(0)的情况  
  
    # 计算透射率和射线点的权重  
    # 透射率是光线通过每个点而不被遮挡的概率的累积乘积  
    transmittance = tf.math.cumprod(expTerm + epsilon, axis=-1, exclusive=True)  
    weights = alpha * transmittance  
      
    # 从射线的点构建图像和深度图  
    # 使用权重和RGB值加权求和得到图像  
    image = tf.reduce_sum(weights[..., None] * rgb, axis=-2)  # 形状变为 [BATCH_SIZE, IMAGE_HEIGHT, IMAGE_WIDTH, 3]  
    # 使用权重和tVals值加权求和得到深度图  
    depth = tf.reduce_sum(weights * tVals, axis=-1)  # 形状变为 [BATCH_SIZE, IMAGE_HEIGHT, IMAGE_WIDTH]  
      
    # 返回渲染后的图像、深度图和权重  
    return (image, depth, weights)

这段代码定义了一个名为 render_image_depth 的函数，其作用是根据由神经网络预测得到的RGB颜色值、体积密度（sigma）和沿射线的采样点（tVals）来渲染图像和深度图。以下是代码的功能描述：

1. 函数定义：

   • 函数接受四个参数：rgb（预测的RGB颜色值），sigma（体积密度），tVals（射线上的采样点）。

2. 参数说明：

   • rgb: 四维张量，形状为 [BATCH_SIZE, IMAGE_HEIGHT, IMAGE_WIDTH, 3]，代表批次中每张图片的RGB颜色值。
   • sigma: 四维张量，形状为 [BATCH_SIZE, IMAGE_HEIGHT, IMAGE_WIDTH, num_samples]，代表每条射线上样本点的体积密度。
   • tVals: 四维张量，形状为 [BATCH_SIZE, IMAGE_HEIGHT, IMAGE_WIDTH, num_samples+1]，代表射线上包括近点和远点的所有采样点的t值。

3. sigma处理：将sigma张量的最后一个维度压缩，以便只考虑每个样本点的体积密度。

4. 计算delta：计算tVals中相邻点之间的差值，用于后续计算沿射线的体积密度的累积效应。

5. 填充delta：在delta张量的最后一维后面添加一个值很大的数（1e10），确保在最后一个样本点之后的alpha值为0。

6. 计算alpha：根据sigma和delta计算alpha值，表示光线在每个样本点处被吸收的比例。

7. 计算累积透射率：使用expTerm和一个小的epsilon值来计算累积透射率，表示光线从视平面的近点到当前点的透射概率。

8. 计算权重：将alpha值与累积透射率相乘，得到每个样本点的权重。

9. 构建图像和深度图：

   • 图像：使用权重对RGB值进行加权求和，得到最终的渲染图像。
   • 深度图：使用权重对tVals进行加权求和，得到每张图片的深度图。

10. 返回结果：函数返回一个包含渲染后的图像、深度图和权重的元组。

此函数是体积渲染过程中的关键步骤，它将神经网络的预测结果转化为可视化的图像和深度信息，为3D场景的理解提供了重要信息。

4.3.光度损失

我们称NeRF使用的损失函数为光度损失。它是通过比较合成图像的颜色与真实图像的颜色来计算的。从数学上讲，这可以表示为：

$$\begin{gathered} \mathcal{L}=\sum _i^N||{\mathcal{I}}_i-{\hat{\mathcal{I}}}_i|{|}_2^2 \\ \mathbf{\theta }={\arg \min }_{\mathbf{\theta }}\mathcal{L} \end{gathered}$$

其中，$\mathcal{I}$是真实图像，$\hat{\mathcal{I}}$ 是合成图像。当这个函数应用于整个流程时，它仍然是完全可微的。这使得我们能够使用反向传播来训练模型参数（$\mathbf{\theta }$）。

5.总结

本文深入探讨了Neural Radiance Fields（NeRF）的核心技术和实现细节，作为“计算机图形和深度学习模型NeRF详解”系列文章的续篇，提供了一个全面而系统的学习路径。NeRF作为一种创新的3D场景重建技术，从有限的2D图像中重建出完整的3D场景，对医学成像、3D场景重建、动画、场景重照明和深度估计等多个领域产生了深远的影响。

5.1.核心概念和算法流程

• NeRF模型：介绍了NeRF的出发点，即从一组特定视角下的图像中合成新视角的图像，涉及新颖图像合成领域。
• 数据输入流程：详细划分了教程内容，包括数据输入流程、射线生成、采样点设置等。
• 多层感知器（MLP）：在NeRF中的应用，预测每个输入采样点的颜色和体积密度。
• 体积渲染技术：利用MLP预测的颜色和体积密度进行3D场景的渲染。
• 光度损失：通过比较合成图像与真实图像的颜色差异来计算损失，优化模型参数。

5.2.实践和代码实现

• 代码示例：提供了代码示例和实践练习，帮助读者深刻理解并应用NeRF技术。
• 源代码下载：提供了源代码的下载链接，方便读者在实践过程中进行参考。

5.3.技术亮点

• 多视角一致性：通过限制网络仅根据位置预测体积密度，同时允许颜色预测考虑位置和观察方向，增强了模型的多视角一致性。
• 实用性强：内容丰富、结构清晰，对于希望深入了解和学习NeRF技术的读者来说，是一份极具价值的资源。

本文不仅阐述了NeRF的理论基础，还通过具体的实现步骤和代码示例，为读者提供了一个从理论到实践的完整指南。随着3D场景重建和计算机图形学技术的不断发展，NeRF及其相关技术将继续在多个领域发挥重要作用。希望本文能为读者在探索NeRF技术的道路上提供坚实的基础和有价值的指导。