[导读]：超平老师的Scratch蓝桥杯真题解读系列在推出之后，受到了广大老师和家长的好评，非常感谢各位的认可和厚爱。作为回馈，超平老师计划推出《Python蓝桥杯真题解析100讲》，这是解读系列的第86讲。

独立农作物区域，本题是2022年4月17日举办的第13届蓝桥杯青少组Python编程省赛真题编程部分第6题，13届一共举办了两次省赛，这是第一次省赛。题目要求对于被划分为N x M块的农田，编程计算出有几块独立的农作物区域。

先来看看题目的要求吧。

一.题目说明

编程实现：

有一块农田被划分为N × M块，农作物和杂草分布生长在农田中，其中农作物使用大写字母R表示，杂草使用大写字母X表示。

请计算出农田中有几块独立的农作物区域（独立的农作物区域指该区域上下左右都被杂草围住，且N × M以外的区域都是杂草）。

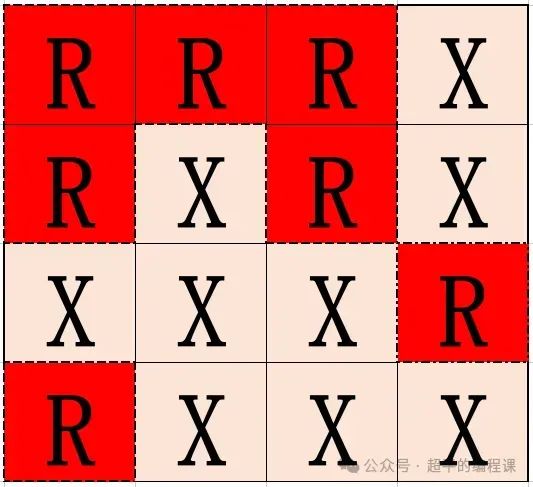
例如：N = 4 , M = 4 , 4 × 4的农田中农作物和杂草分布如下图，这块4 × 4的农田中有3块独立的农作物区域（红色的3部分）。

输入描述：

第一行输入两个整数N和M（1 ≤ N ≤ 100 ， 1 ≤ M ≤ 100 ），N表示农田的行数，M表示农田的列数，且两个正整数之间以一个英文逗号隔开。

接下来的N行每行包括M个字符（字符只能为R或X），R表示农作物，X表示杂草，字符之间以一个英文逗号隔开。

输出描述：

输出一个整数，表示N × M的农田中有几块独立的农作物区域。

输入样例：

4, 4

R, R, R, X

R, X, R, X

X, X, X, R

R, X, X, X

输出样例：

3

二.思路分析

这是一道经典的算法题，涉及的知识点包括循环、条件、二维列表、枚举算法、递归和DFS算法等。

这其实是一个经典的岛屿问题，什么是岛屿问题呢？

对于本题中所描述的调整规则，如何保证调整次数最少呢，这其中又有什么规律和奥妙呢？

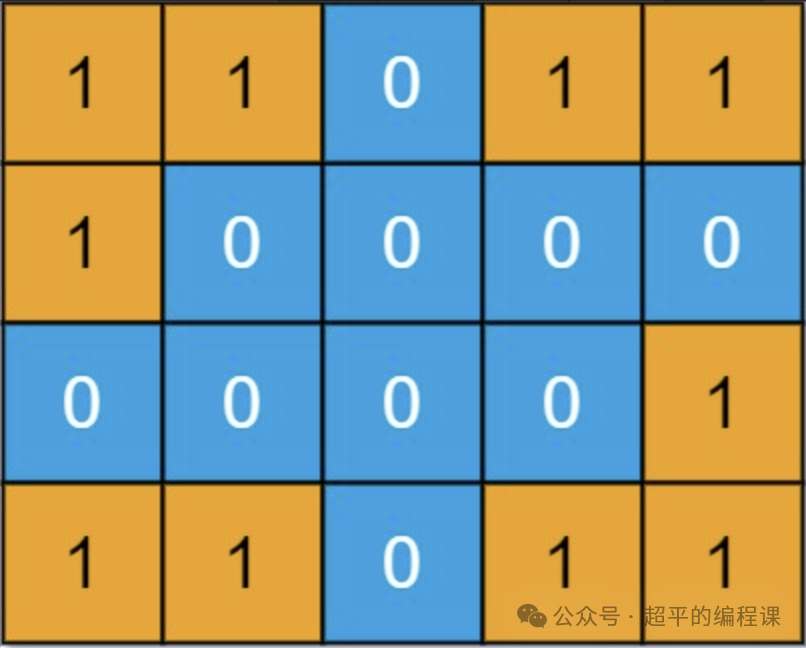
岛屿问题是一类与图、矩阵等数据结构相关的计算机科学问题，通常涉及在由1和0组成的二维矩阵中寻找连接在一起的'1'（代表陆地）形成的岛屿的数量、面积或其他特征。

岛屿问题的典型场景是给定一个二维矩阵，其中1表示陆地，0表示水域，岛屿是由水平和垂直连接的陆地格子组成的。

岛屿问题通常可以细分为以下几类：

• 计算岛屿数量：给定一个二维矩阵，计算其中岛屿的数量，即由'1'组成的相连区域的个数。

• 计算岛屿面积：在给定的二维矩阵中，计算每个岛屿的面积是多少，即由'1'组成的区域的格子数。

• 最大岛屿面积：在二维网格上找到最大的岛屿，即具有最大面积的岛屿。

• 判断岛屿边界：判断岛屿的周围是否有水域，即判断岛屿的边界情况。

本题描述的场景，就是第一种，只不过这里用R表示农作物，X表示杂草，要计算的是农作物区域的数量，其本质是一样的。

解决岛屿问题，通常会使用如下3种经典算法：

• 深度优先搜索（DFS）：通过深度优先搜索算法遍历二维网格中的每个格子，对未访问的陆地格子进行深度优先搜索，以识别形成的岛屿。

• 广度优先搜索（BFS）：使用广度优先搜索算法，从陆地格子开始向外层扩展，以识别和计算岛屿。

• 并查集（Union Find）：使用并查集数据结构来表示不同区域的连接情况，以组织和计算岛屿数量。

其中，DFS算法相对更简单和直观，理解起来也比较容易，对于初学者来说是最佳选择，所以，超平老师将重点介绍DFS算法的实现方法。

DFS，即深度优先搜索，是Depth First Search的简写，它是一种用于遍历或搜索树或图的算法，早在19世纪就被用于解决迷宫问题。

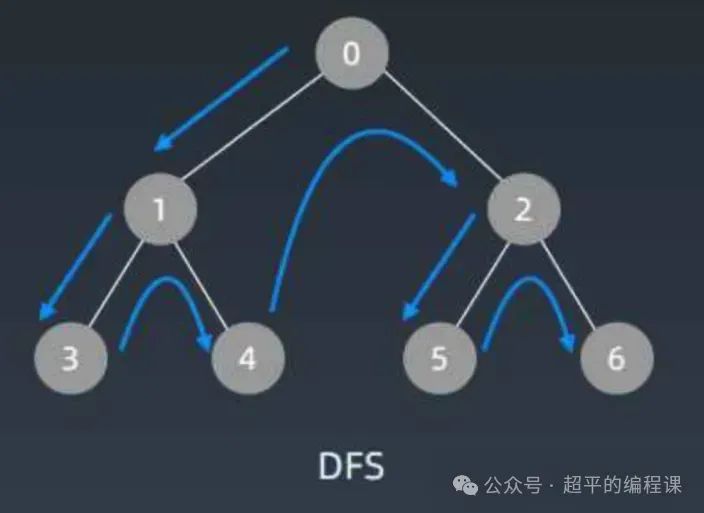
DFS算法的核心思想是尽可能深地探索图的分支，直到无法继续为止，然后回溯并探索其他分支，在代码层面，主要是通过递归来实现。

为了更好地理解DFS过程，我们举例来说明，以第一个单元格grid[0][0]为例，如下：

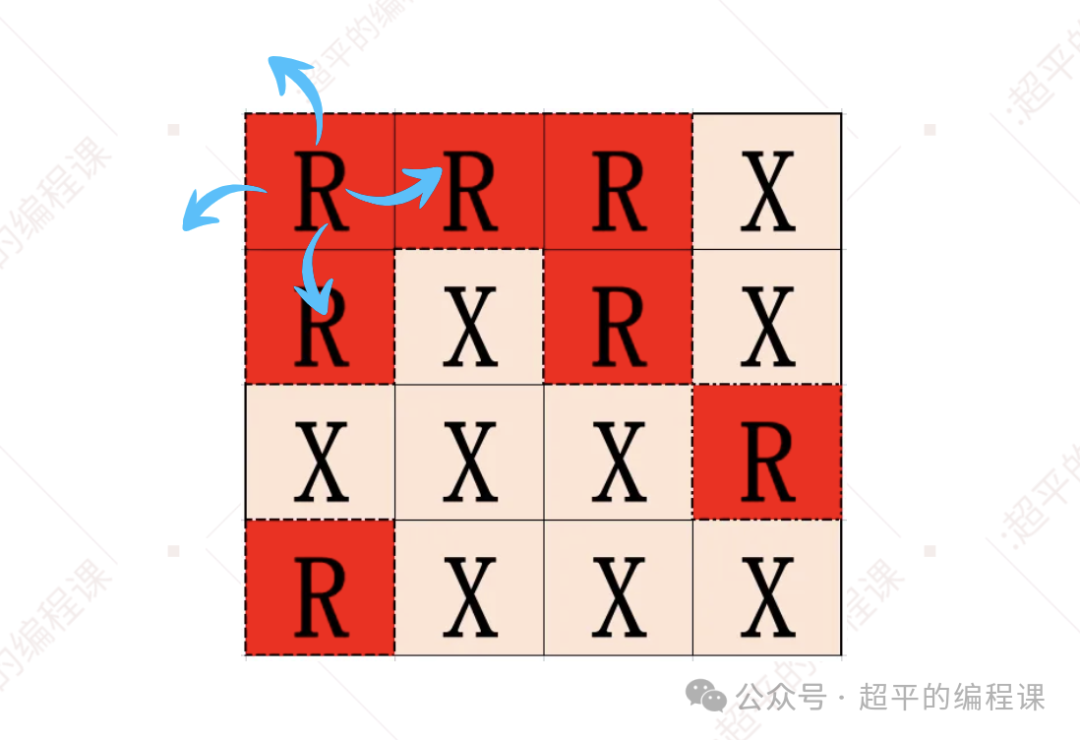
grid[0][0] = "R"，生长的是农作物，说明找到了一块农作物区域，因此我们需要将它周围的农作物单元格都找出来。

这就需要沿着4个方向进行搜索，如下：

• 左：左边没有单元格了，直接返回；

• 上：上面也没有单元格了，直接返回；

• 右：右边的单元格是农作物R，就以同样的方式递归处理；

• 下：下边的单元格是农作物R，以同样的方式递归处理；

先处理右方grid[0][1]，它也需要向上下左右4个方向进行搜索，如图：

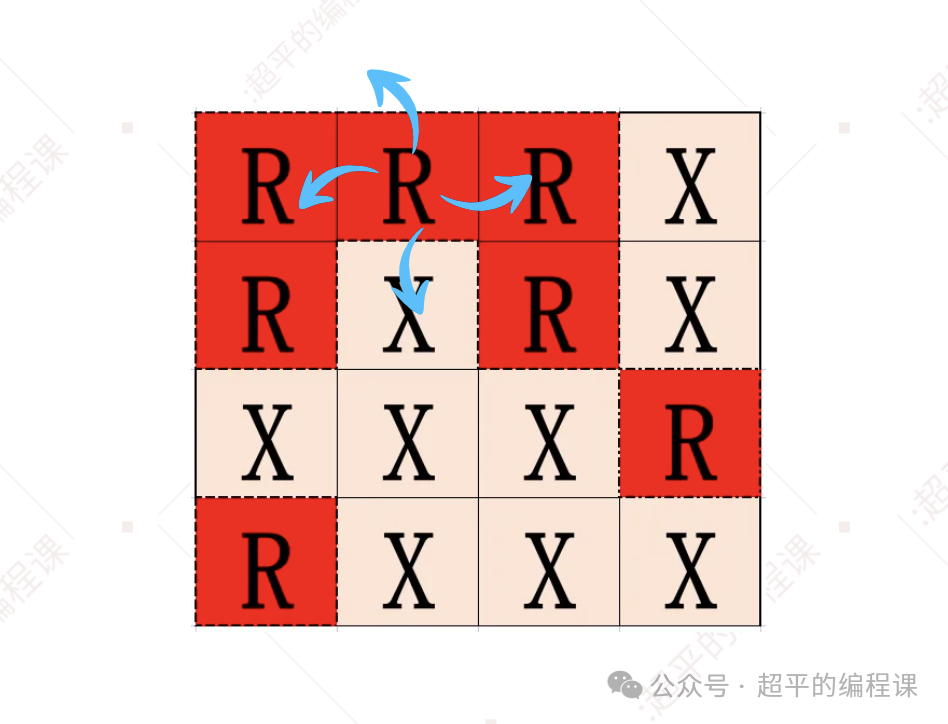
这时会遇到一个非常棘手的问题，它左边的单元格grid[0][0]已经处理过了，如果再向左搜索，就会陷入死循环。

因此，我们在处理grid[0][0]时，就需要将其变成X，也就是常说的淹掉（或者感染），如图：

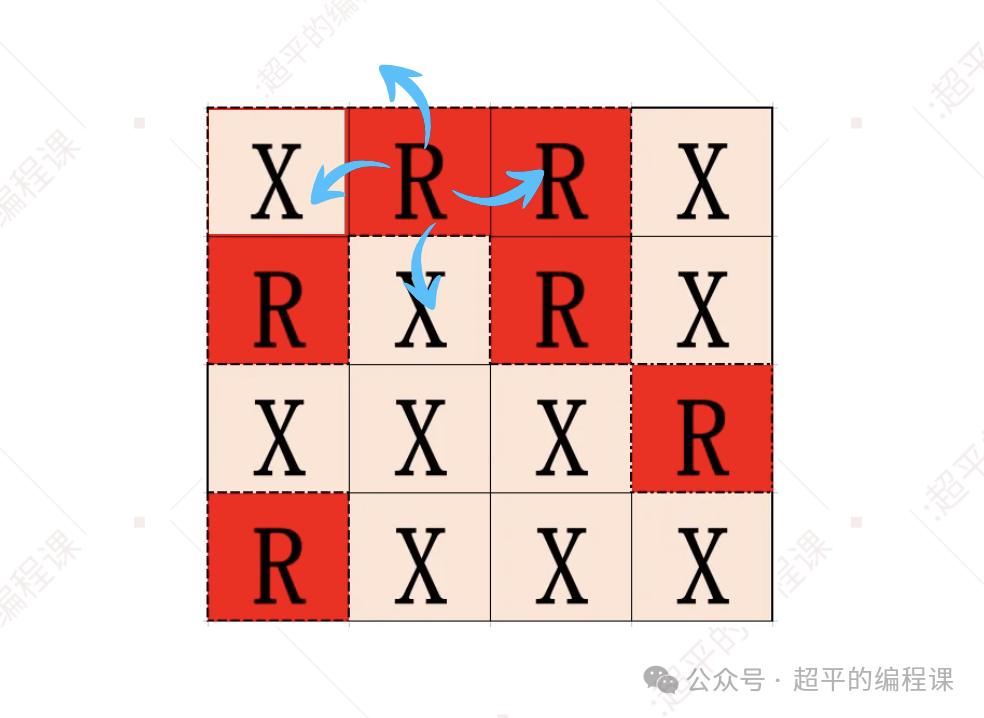
对于单元格grid[0][1]，继续沿着4个方向进行搜索，如下：

• 左：左边的单元格是草地X，直接返回；

• 上：上面也没有单元格了，直接返回；

• 右：右边的单元格是农作物R，以同样的方式递归处理；

• 下：下边的单元格是草地X，直接返回；

同时，将当前单元格grid[0][1]也变成草地X，然后递归处理右边的单元格grid[0][2]，如图：

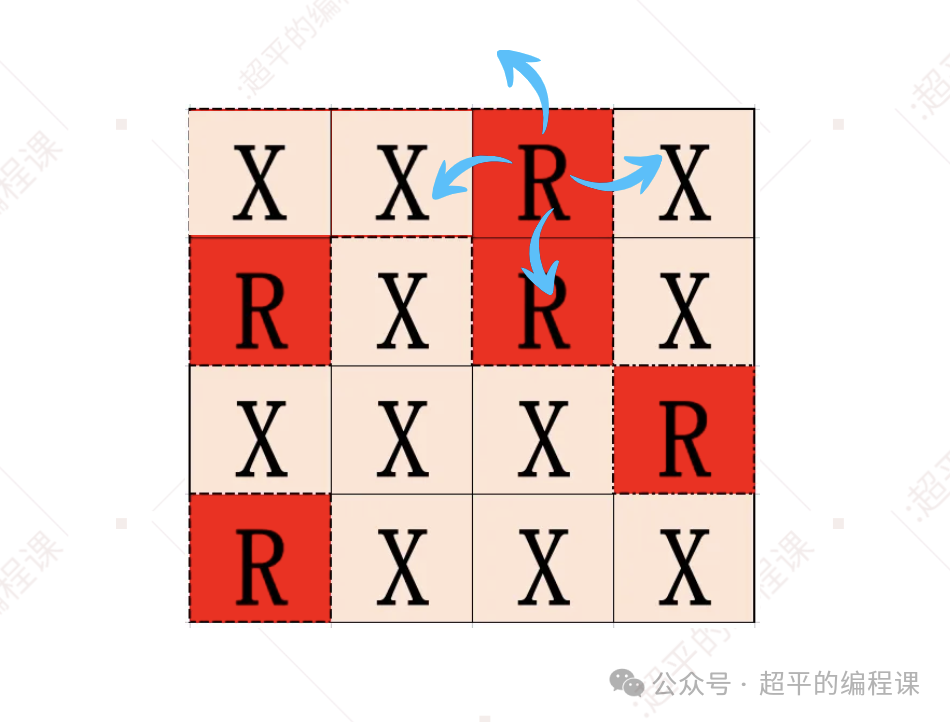
仍然沿着4个方向进行搜索，如下：

• 左：左边的单元格是草地X，直接返回；

• 上：上面也没有单元格了，直接返回；

• 右：右边的单元格是草地X，直接返回；

• 下：下边的单元格是农作物R，以同样的方式递归处理；

将当前单元格grid[0][2]淹掉，变成草地X，然后再递归处理下边的单元格grid[1][2]，如图：

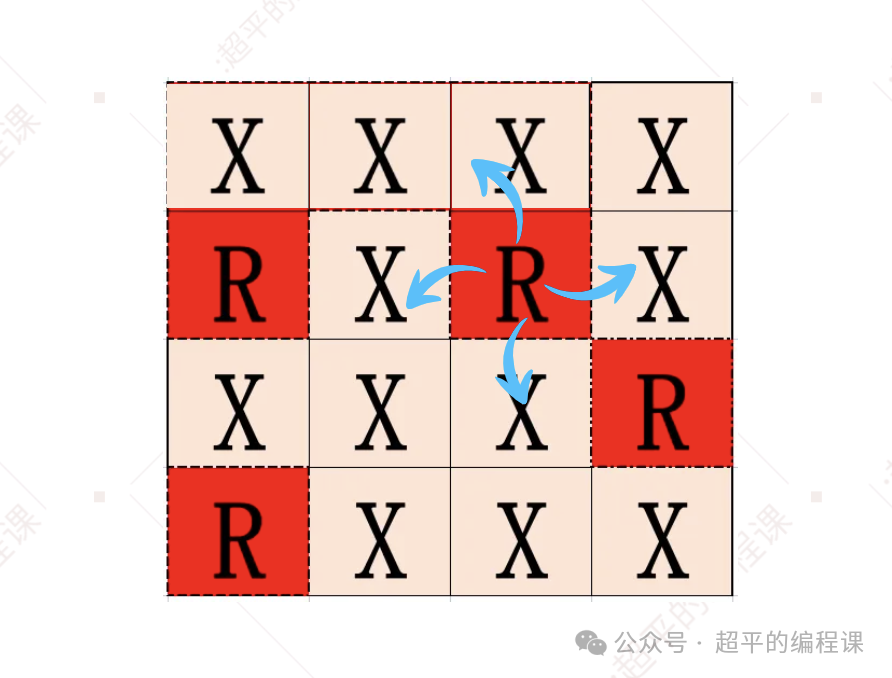
还是沿着4个方向进行搜索，此时四周全都是草地X，直接返回，同时将当前单元格grid[1][2]淹掉，变成草地X。

然后再回到grid[0][0]，处理它下方的单元格grid[1][0]，如图：

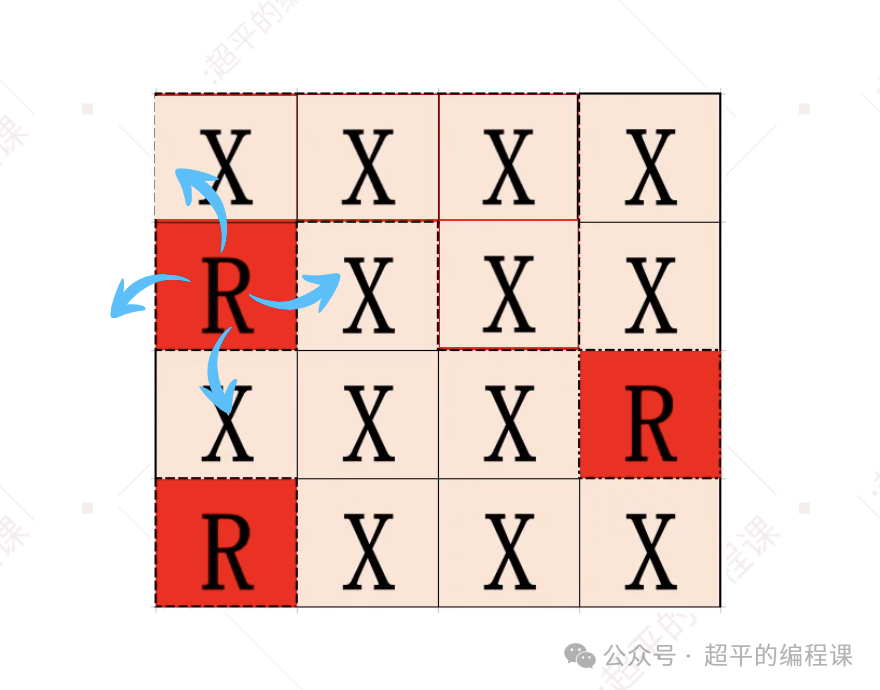
对于grid[1][0]来说，左边没有单元格，其它3个方向都是草地X，直接返回，同时将当前单元格grid[1][0]淹掉，变成草地X，如图：

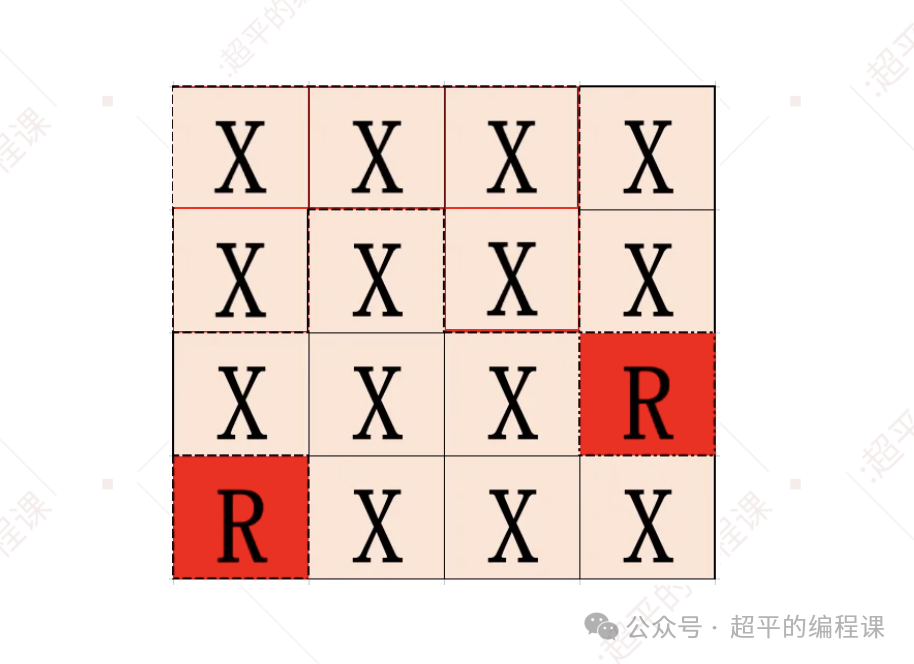
如此一来，第一块农作物区域就处理完了，然后再以同样的方式来处理其他的农作物区域。

注意，在处理每一个单元格的时候，都需要沿着4个方向进行搜索，对于每个方向，都会重复同样的操作，一搜到底，颇有点不到黄河心不死的味道，这就是DFS算法的精髓。

思路有了，接下来，我们就进入具体的编程实现环节。

三.编程实现

根据上面的思路分析，我们分两步编写程序：

• 定义DFS函数

• 统计农作物区域数量

1. 定义DFS函数

根据前面的思路分析，定义DFS函数如下：

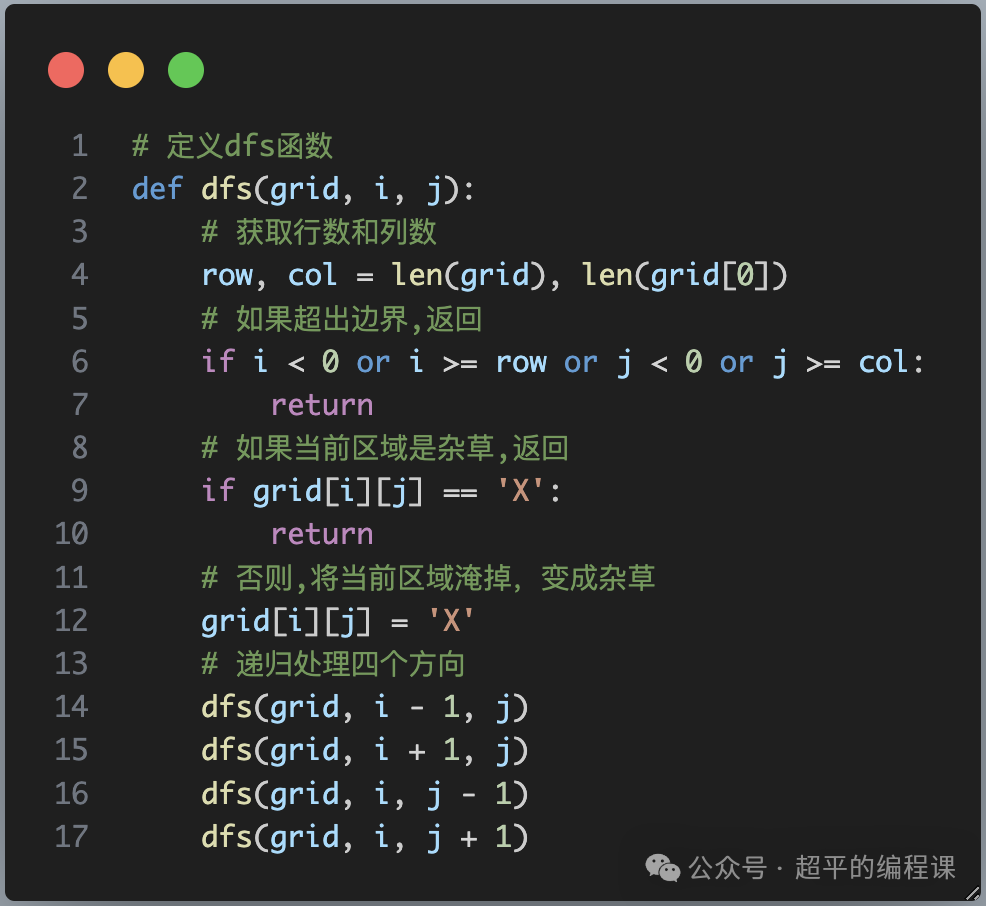
代码不多，强调3点：

1). 要彻底理解DFS函数的真实含义，它的作用是对于二维表格中的单元格(i, j)，如果是农作物区域（字符为R），则将和它连在一起的所有单元格都变成杂草区域（字符为X），这就是所谓淹掉函数（感染函数）的含义；

2). 对于给定的i和j，需要考虑两个特殊情况，一是越界了，二是当前区域是杂草，它们是递归函数的出口，两个条件的顺序很重要，不能颠倒，否则会出现越界错误，也可以合并为一个条件，如下：

if i < 0 or i >= row or j < 0 or j >= col or grid[i][j] == 'X'

3). 一旦发现当前单元格是农作物（R），那么就将其淹掉，变成杂草（X），然后通过递归，将一整片农作物区域都变成杂草，从而避免重复处理，陷入死循环。

2. 统计农作物区域数量

有了DFS函数，就可以按照从上到下、从左到右的顺序遍历每一个单元格，代码如下：

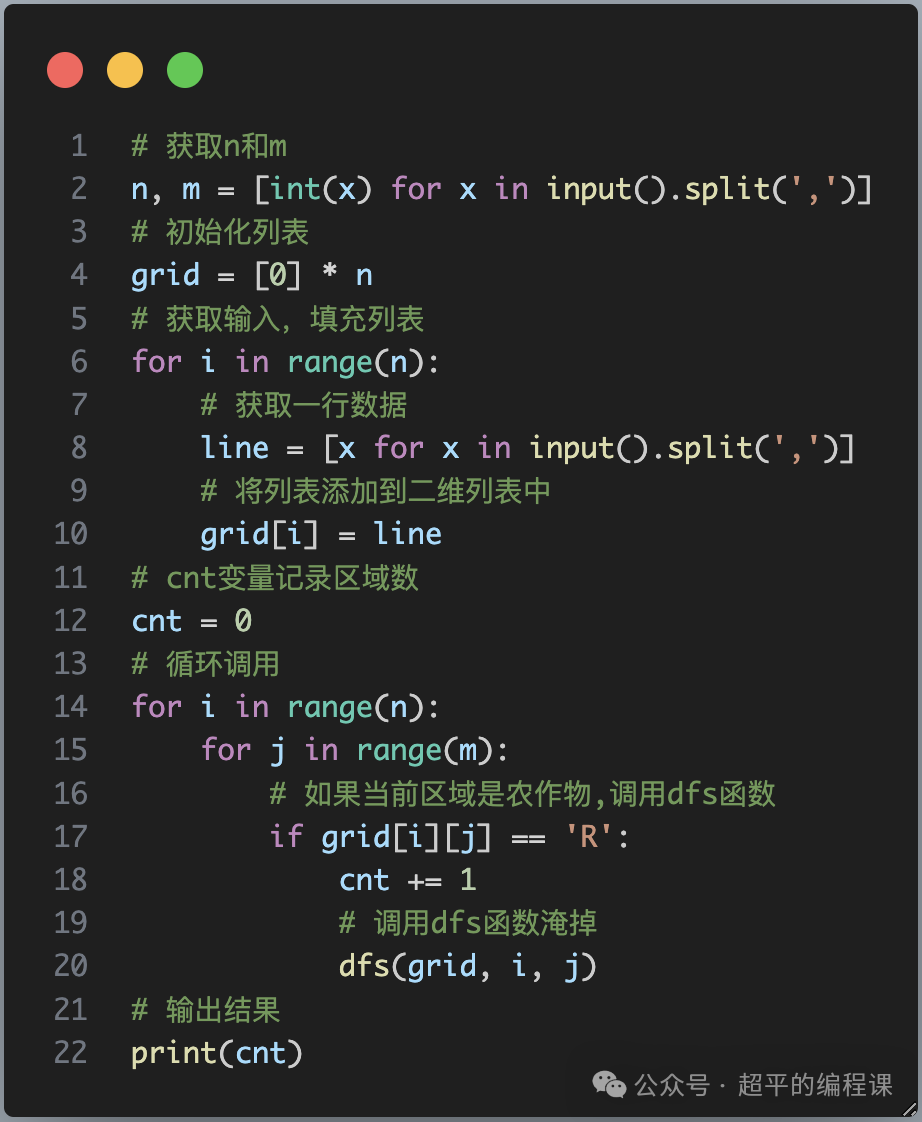
代码不算多，说明两点：

1). grid是一个n x m的二维列表，先通过循环获取输入的n行字符；

2). 统计农作物区域时，需要遍历每一个单元格，如果当前区域是农作物，就说明找到了一块农作物区域，将cnt增加1，然后调用dfs函数将这一片农作物都淹掉，变成杂草。

至此，整个程序就全部完成了，你可以输入不同的数据来测试效果啦。

四.总结与思考

本题代码在23行左右，涉及到的知识点包括：

• 循环语句；

• 条件语句；

• 二维列表；

• 枚举算法；

• 递归函数；

• DFS算法；

作为本次测评的最后一题，本题代码不少，难度也比较大。关键点有两个，一是对递归函数的理解和运用，二是对DFS函数的深入理解。

递归是一种强大的机制，它本身就能够帮我们做很多事情，我们只需要确定两点，一是如何进行递归，二是递归的结束条件。

对于岛屿问题，递归是向上下左右4个方向进行的，结束条件也非常简单，就是一旦越界，立刻结束。

DFS函数是本题的重点，我们不能仅仅停留在具体的代码层面，而是要将其抽象出来，深入理解其作用。

为了更好的理解，建议大家多使用淹掉函数（或感染函数）来描述，形象生动，便于理解。

实际上，所有岛屿问题的解决方法都是类似的，而DFS函数是解决这类问题的关键。因此，一定要深入理解并掌握DFS函数的定义及使用。

岛屿问题不仅在计算机科学领域中常见，还在地理信息系统、图像分析、游戏开发等领域有着广泛的应用。

你还有什么好的想法和创意吗，也非常欢迎和超平老师分享探讨。

如果你觉得文章对你有帮助，别忘了点赞和转发，予人玫瑰，手有余香😄

需要源码的，可以移步至“超平的编程课”gzh。