【Python机器学习实战】 | 基于空气质量监测数据，采用多层神经网络预测PM2.5浓度

🎩 欢迎来到技术探索的奇幻世界👨‍💻

📜 个人主页：@一伦明悦-CSDN博客

✍🏻 作者简介： C++软件开发、Python机器学习爱好者

🗣️ 互动与支持：💬评论 👍🏻点赞 📂收藏 👀关注+

如果文章有所帮助，欢迎留下您宝贵的评论，

点赞加收藏支持我，点击关注，一起进步！

引言

多层网络是一种深度学习模型，也称为深度神经网络（Deep Neural Network, DNN）。它由多个神经网络层（或称为隐藏层）组成，每一层包含多个神经元（或节点），用于逐层提取和学习输入数据的特征表示。

结构与组成

输入层（Input Layer）：

接收原始数据作为输入，每个特征通常对应输入层中的一个节点。输入层的节点数量由数据的特征维度决定。

隐藏层（Hidden Layers）：

在输入层和输出层之间的层级称为隐藏层。每个隐藏层由多个神经元组成，每个神经元与上一层的所有神经元相连，形成完全连接（全连接）的结构。隐藏层的数量和每层的神经元数量是多层网络的核心组成部分。
每个隐藏层通过激活函数（如ReLU、Sigmoid等）对输入进行非线性变换，使得网络能够学习非线性关系和复杂模式。

输出层（Output Layer）：

提供最终的预测或分类结果。输出层的神经元数量通常取决于问题的需求，如二分类问题可能只有一个神经元输出概率，多分类问题则有多个神经元对应不同类别的概率。

工作原理

前向传播（Forward Propagation）：

输入数据从输入层经过每个隐藏层到达输出层的过程。每一层的输出作为下一层的输入，通过权重矩阵和偏置向量进行线性变换，并经过激活函数得到非线性变换的结果。

反向传播（Backward Propagation）：

通过损失函数衡量模型预测与真实值的差异，然后利用反向传播算法调整每一层的权重和偏置，从而最小化损失函数。这一过程使用梯度下降法或其变种来更新网络参数。

主要优势

学习复杂特征：多层网络能够学习数据中的多层次特征表示，从而提升模型对复杂模式和关系的表达能力。

非线性建模：通过每层的非线性激活函数，多层网络能够处理非线性关系，适用于各种复杂的数据分布和任务。

自动特征学习：通过层层传递学习，网络可以自动发现和提取数据中的高级特征，减少手工特征工程的需求。

应用领域

图像识别与处理：如卷积神经网络（CNN）在图像分类、目标检测等任务中的广泛应用。

自然语言处理：如循环神经网络（RNN）和其变种（如长短时记忆网络LSTM）在语言建模、文本生成等方面的成功应用。

推荐系统：通过学习用户行为和物品特征，提供个性化推荐。

多层网络作为深度学习的基础模型，在各种领域都展示了强大的建模能力和应用潜力，对于处理复杂的数据和任务具有重要意义。

正文

01-直观展示不同激活函数下输入变量和输出变量间的关系

这段代码是用来展示神经网络中常见的激活函数对应的分类或回归面的可视化效果。以下是对代码各部分的详细解释：
导入模块和设置绘图参数
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
导入必要的库，包括NumPy用于数值计算，Matplotlib用于绘图，以及Matplotlib的3D绘图工具。
import warnings
warnings.filterwarnings(action='ignore')
%matplotlib inline
plt.rcParams['font.sans-serif'] = ['SimHei']  # 解决中文显示乱码问题
plt.rcParams['axes.unicode_minus'] = False
设置绘图环境，包括忽略警告、内联显示图形、设置中文字体和解决负号显示问题。
绘制Logistic函数
v = np.linspace(-10, 10, 100)
y = 1 / (1 + np.exp(-v))
plt.plot(v, y)
plt.xlabel("V")
plt.ylabel("1 / (1 + np.exp(-V))")
plt.grid(True, linestyle='-.')
plt.savefig("../4.png", dpi=500)
绘制Logistic函数的图像，用于展示激活函数的典型形式，以及如何处理输入v。
绘制三种激活函数对应的分类或回归面
x1 = np.linspace(-5, 5, 20)
x2 = np.linspace(-5, 5, 20)
X1, X2 = np.meshgrid(np.linspace(x1.min(), x1.max(), 20), np.linspace(x2.min(), x2.max(), 20))
创建二维网格数据，用于在X1和X2平面上绘制三维图形。
w = [1/np.sqrt(2), 1/np.sqrt(2)]
V = w[0]*X1 + w[1]*X2 + 0.5
Y = 1 / (1 + np.exp(-V))
绘制Logistic激活函数的分类或回归面。其中，V是感知机模型中的线性组合，Y是Logistic函数应用于V后的输出。
fig = plt.figure(figsize=(20, 6))
ax1 = fig.add_subplot(131, projection='3d')
ax1.plot_wireframe(X1, X2, Y, linewidth=0.5)
ax1.plot_surface(X1, X2, Y, alpha=0.3)
ax1.set_xlabel('X1')
ax1.set_ylabel('X2')
ax1.set_zlabel('Y')
ax1.set_title('感知机的分类或回归面(logistic激活函数)')
创建一个包含三个子图的大图，分别展示Logistic、tanh和ReLU激活函数对应的分类或回归面。
Y = (np.exp(V) - np.exp(-V)) / (np.exp(V) + np.exp(-V))
ax2 = fig.add_subplot(132, projection='3d')
ax2.plot_wireframe(X1, X2, Y, linewidth=0.5)
ax2.plot_surface(X1, X2, Y, alpha=0.3)
ax2.set_xlabel('X1')
ax2.set_ylabel('X2')
ax2.set_zlabel('Y')
ax2.set_title('感知机的分类或回归面(tanh激活函数)')
绘制tanh激活函数对应的分类或回归面。
Y = np.zeros((V.shape))
id = np.where(V > 0)
Y[id] = V[np.where(V > 0)]
ax3 = fig.add_subplot(133, projection='3d')
ax3.plot_wireframe(X1, X2, Y, linewidth=0.5)
ax3.plot_surface(X1, X2, Y, alpha=0.3)
ax3.set_xlabel('X1')
ax3.set_ylabel('X2')
ax3.set_zlabel('Y')
ax3.set_title('感知机的分类或回归面(relu激活函数)')
plt.savefig("../4.png", dpi=500)
绘制ReLU激活函数对应的分类或回归面。在这里，Y根据ReLU的定义来确定每个点的值。
通过这些代码，可以直观地展示不同激活函数如何影响神经网络的输出结果，以及它们在处理不同数据模式时的表现。

#本章需导入的模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pylab import *
import matplotlib.cm as cm
import warnings
warnings.filterwarnings(action = 'ignore')
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.metrics import zero_one_loss,r2_score,mean_squared_error
import sklearn.neural_network as net

v=np.linspace(-10,10,100)
y=1/(1+np.exp(-v))
plt.plot(v,y)
plt.xlabel("V")
plt.ylabel("1/(1+np.exp(-V))")
plt.grid(True, linestyle='-.')
plt.savefig("../4.png", dpi=500)   

x1=np.linspace(-5,5,20)
x2=np.linspace(-5,5,20)
X1,X2= np.meshgrid(np.linspace(x1.min(),x1.max(),20), np.linspace(x2.min(),x2.max(),20))
w=[1/np.sqrt(2),1/np.sqrt(2)]
V=w[0]*X1+w[1]*X2+0.5
Y=1/(1+np.exp(-V))
fig = plt.figure(figsize=(20,6))
ax1 = fig.add_subplot(131, projection='3d')      
ax1.plot_wireframe(X1,X2,Y,linewidth=0.5)
ax1.plot_surface(X1,X2,Y,alpha=0.3)
ax1.set_xlabel('X1')
ax1.set_ylabel('X2')
ax1.set_zlabel('Y')
ax1.set_title('感知机的分类或回归面(logistic激活函数)')

Y=(np.exp(V)-np.exp(-V))/(np.exp(V)+np.exp(-V))
ax2 = fig.add_subplot(132, projection='3d')      
ax2.plot_wireframe(X1,X2,Y,linewidth=0.5)
ax2.plot_surface(X1,X2,Y,alpha=0.3)
ax2.set_xlabel('X1')
ax2.set_ylabel('X2')
ax2.set_zlabel('Y')
ax2.set_title('感知机的分类或回归面(tanh激活函数)')
#fig.subplots_adjust(hspace=0.5)
fig.subplots_adjust(wspace=0)

Y=np.zeros((V.shape))
id=np.where(V>0)
Y[id]=V[np.where(V>0)]
ax3 = fig.add_subplot(133, projection='3d')      
ax3.plot_wireframe(X1,X2,Y,linewidth=0.5)
ax3.plot_surface(X1,X2,Y,alpha=0.3)
ax3.set_xlabel('X1')
ax3.set_ylabel('X2')
ax3.set_zlabel('Y')
ax3.set_title('感知机的分类或回归面(relu激活函数)')
plt.savefig("../4.png", dpi=500)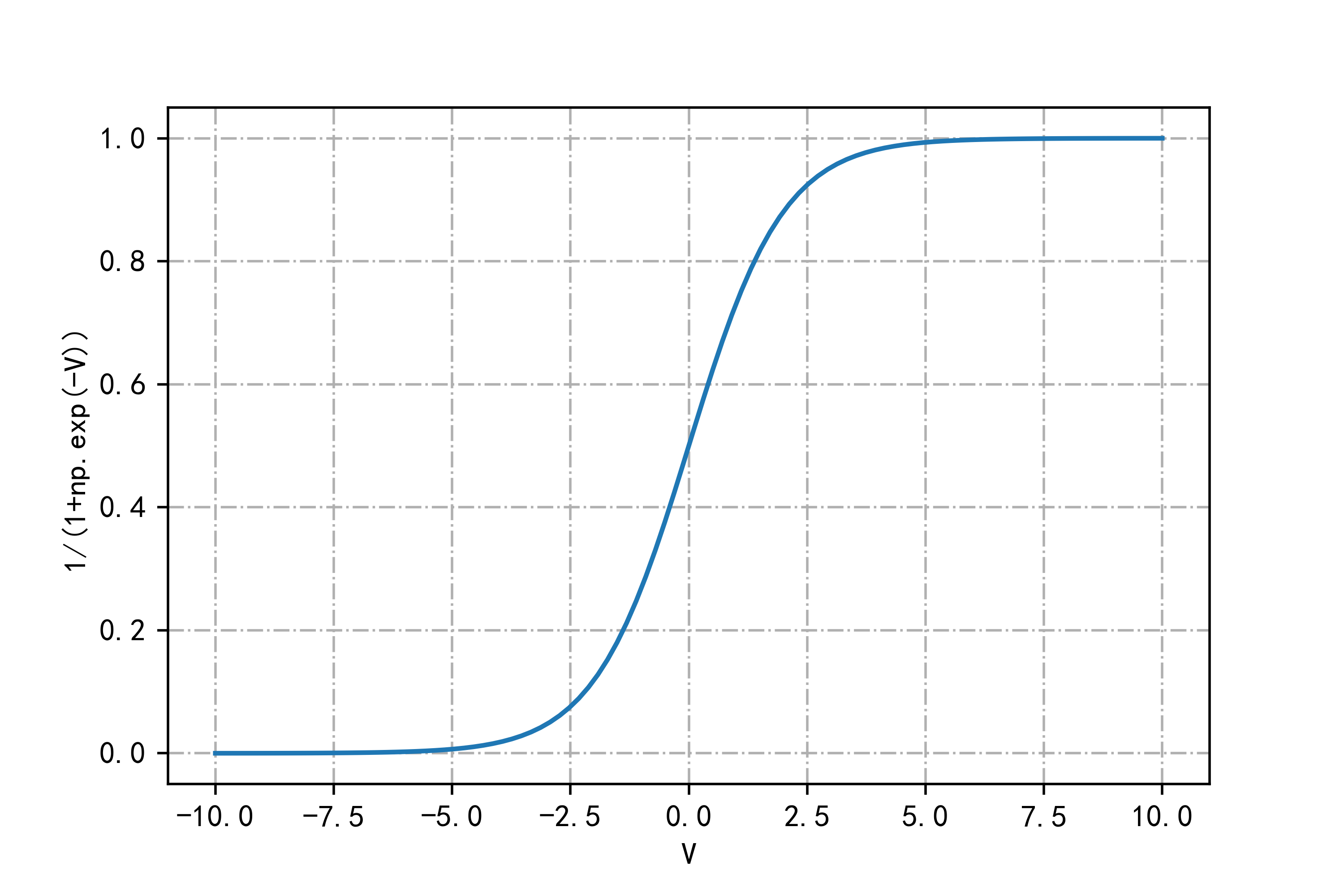

02-多层感知机的分类边界

这段代码是用来演示多层感知机（MLP）在二维空间中的分类边界。让我们逐步解释代码的作用：

导入模块：

numpy, pandas, matplotlib.pyplot, pylab等常见数据处理和可视化模块。
matplotlib.cm 用于颜色映射。
warnings 用于忽略警告信息。
%matplotlib inline 设置 Jupyter Notebook 中的图形直接显示。
plt.rcParams 设置字体和坐标轴显示参数。
Axes3D 是用于绘制三维图形的类。
make_circles 是用来生成环形数据集的函数。
其他是用于评估模型性能的指标和导入多层感知机模型的类。

生成数据集：

使用 make_circles 函数生成包含两类样本的环形数据集 X 和对应的标签 Y。

设置网格数据：

使用 meshgrid 创建二维平面网格 X1, X2，用于绘制分类边界。

创建子图和颜色映射：

使用 plt.subplots 创建包含4个子图的图形窗口，每个子图展示不同的模型配置。
plt.cm.Spectral 用于生成一组颜色，用于绘制数据点和分类边界。
markers 列表定义了用于不同类别数据点的标记形状。

循环不同的神经网络配置：

使用 for 循环迭代不同的隐藏层节点数目和子图位置 (H, L)。
对于每个配置 (hn, H, L)：
创建 MLPClassifier 模型，并用环形数据 X, Y 进行拟合。
预测网格上的所有点 X0 的分类结果 Y0。
在子图中绘制预测结果，其中每个类别用不同颜色表示，背景为灰色或者玫瑰色。

子图设置和保存：

设置每个子图的标题、坐标轴标签和背景数据点的显示。
最后通过 plt.savefig 将绘制好的图形保存为文件。

总体来说，这段代码展示了如何使用多层感知机模型对环形数据进行分类，并通过不同配置的模型展示了不同的分类边界效果，同时通过可视化帮助理解神经网络在数据分类任务中的应用和效果。

#本章需导入的模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pylab import *
import matplotlib.cm as cm
import warnings
warnings.filterwarnings(action = 'ignore')
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.metrics import zero_one_loss,r2_score,mean_squared_error
import sklearn.neural_network as net

N=800
X,Y=make_circles(n_samples=N,noise=0.2,factor=0.5,random_state=123)
unique_lables=set(Y)
X1,X2= np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),50),np.linspace(X[:,1].min(),X[:,1].max(),50))
X0=np.hstack((X1.reshape(len(X1)*len(X2),1),X2.reshape(len(X1)*len(X2),1)))

fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(15,12))
colors=plt.cm.Spectral(np.linspace(0,1,len(unique_lables)))
markers=['o','*']
for hn,H,L in [(1,0,0),(2,0,1),(4,1,0),(30,1,1)]:
    NeuNet=net.MLPClassifier(hidden_layer_sizes=(hn,),random_state=123)
    NeuNet.fit(X,Y)
    Y0=NeuNet.predict(X0)
    axes[H,L].scatter(X0[np.where(Y0==0),0],X0[np.where(Y0==0),1],c='mistyrose')
    axes[H,L].scatter(X0[np.where(Y0==1),0],X0[np.where(Y0==1),1],c='lightgray')
    axes[H,L].set_xlabel('X1')
    axes[H,L].set_ylabel('X2')
    axes[H,L].set_title('多层感知机的分类边界(层数=%d,隐藏节点数=%d,错误率=%.2f)'%(NeuNet.n_layers_,hn,1-NeuNet.score(X,Y)))
    for k,col,m in zip(unique_lables,colors,markers):
        axes[H,L].scatter(X[Y==k,0],X[Y==k,1],color=col,s=30,marker=m) 
plt.savefig("../4.png", dpi=500)

运行结果如下图所示：

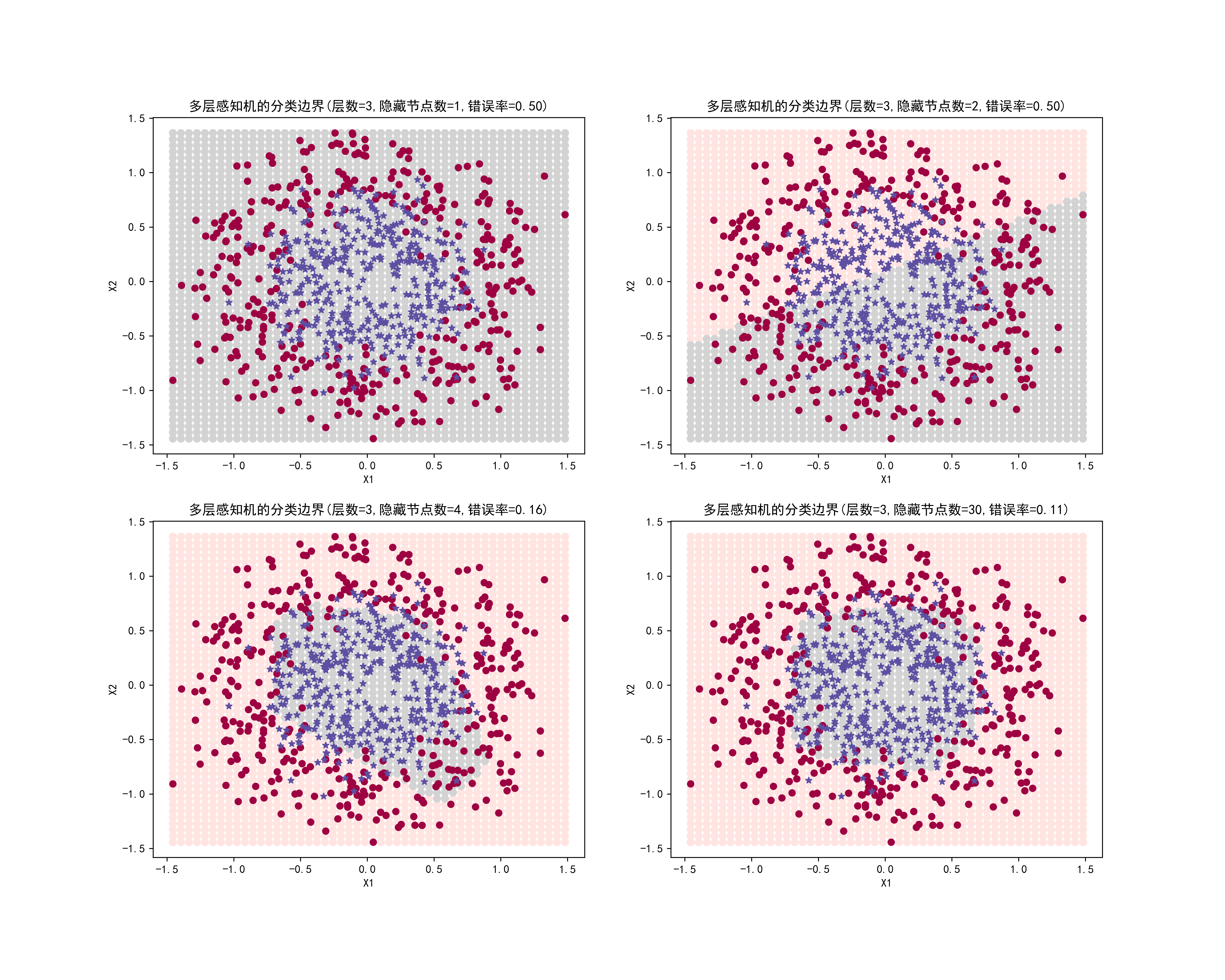
03-可视化手写体阿拉伯数字

这段代码主要用于分析多层感知机（MLP）在处理手写数字数据集（邮政编码数据）时的表现，以及不同配置下隐藏层节点数对模型性能的影响。

导入模块：

导入了常用的数据处理、可视化和机器学习模块，如 numpy, pandas, matplotlib.pyplot 等。
使用 matplotlib.cm 和 pylab 进行颜色映射和图形显示设置。
忽略了警告信息以及设置了中文显示的相关参数。

读取数据集：

使用 pd.read_table 从文件 ‘邮政编码数据.txt’ 中读取数据，该数据集包含手写数字的像素数据。
分别将特征 X 和标签 Y 提取出来，其中 X 是像素特征，Y 是对应的数字标签。

显示部分样本：

随机选择25个样本，并以5x5的子图形式展示在一个大图中。
每个子图显示一个手写数字的灰度图像，使用 plt.imshow 函数展示像素数据。

划分训练集和测试集：

使用 train_test_split 函数将数据集划分为训练集和测试集，其中训练集占60%。
X_train, X_test, Y_train, Y_test 分别是训练集和测试集的特征和标签。

模型训练与评估：

针对不同的隐藏层节点数 nodes 和激活函数 acts 进行组合，使用 for 循环进行训练和评估。
对于每个节点数 node 和激活函数 act：
创建 MLPClassifier 模型，并在训练集上拟合。
计算并记录训练误差和测试误差（错误率）到 errTrain 和 errTest 数组中。

绘制误差曲线：

使用 plt.plot 绘制隐藏节点数 nodes 与训练误差、测试误差的关系曲线。
曲线分为两种激活函数 (relu 和 logistic) 下的训练误差和测试误差。
添加标题、坐标轴标签、刻度和图例，最终通过 plt.savefig 将图形保存为文件。

综上所述，这段代码展示了如何使用多层感知机模型处理手写数字数据集，通过不同的节点数和激活函数组合，分析和比较模型在训练和测试数据上的表现，帮助选择最优的模型配置。

#本章需导入的模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pylab import *
import matplotlib.cm as cm
import warnings
warnings.filterwarnings(action = 'ignore')
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.metrics import zero_one_loss,r2_score,mean_squared_error
import sklearn.neural_network as net

data=pd.read_table('邮政编码数据.txt',sep=' ',header=None)
X=data.iloc[:,1:-1]
Y=data.iloc[:,0]
#print(Y.unique())
np.random.seed(1)
ids=np.random.choice(len(Y),25)
plt.figure(figsize=(8,8))
for i,item in enumerate(ids):
    img=np.array(X.iloc[item,]).reshape((16,16))
    plt.subplot(5,5,i+1)
    plt.imshow(img,cmap=cm.gray_r)
plt.show()
plt.savefig("../4.png", dpi=500)  

X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.60, random_state=123)
#NeuNet=net.MLPClassifier(activation='logistic',solver='sgd',batch_size=50)
nodes=np.arange(1,20,2)
acts=['relu','logistic']
errTrain=np.zeros((len(nodes),2))
errTest=np.zeros((len(nodes),2))
for i,node in enumerate(nodes):
    for j,act in enumerate(acts):
        NeuNet=net.MLPClassifier(hidden_layer_sizes=(node,),activation=act,random_state=1)
        NeuNet.fit(X_train,Y_train)
        errTrain[i,j]=1-NeuNet.score(X_train,Y_train)
        errTest[i,j]=1-NeuNet.score(X_test,Y_test)
        
plt.plot(nodes,errTest[:,0],label="relu激活(测试误差)",linestyle='-')
plt.plot(nodes,errTest[:,1],label="logistic激活(测试误差)",linestyle='-.')
plt.plot(nodes,errTrain[:,0],label="relu激活(训练误差)",linestyle='-',linewidth=0.5)
plt.plot(nodes,errTrain[:,1],label="logistic激活(训练误差)",linestyle='-.',linewidth=0.5)
plt.title('隐藏节点数与误差')
plt.xlabel('隐藏节点数')
plt.ylabel('误差')
plt.xticks(nodes)
plt.legend()
plt.savefig("../4.png", dpi=500)

运行结果如下图所示：

04-基于空气质量监测数据，采用多层神经网络预测PM2.5浓度

这段代码主要用于分析多层感知机（MLP）在处理北京市空气质量数据时的表现，比较不同激活函数（ReLU和Logistic）下模型的损失曲线和性能评估。

导入模块：

导入了必要的数据处理、可视化和机器学习模块，如 numpy, pandas, matplotlib.pyplot 等。
设置了中文显示和解决负号显示问题的参数。

读取和预处理数据集：

使用 pd.read_excel 从文件 ‘北京市空气质量数据.xlsx’ 中读取数据。
进行数据预处理，将0值替换为NaN，并删除含有NaN的行，同时筛选出符合条件的数据（PM2.5 <= 200 和 SO2 <= 20）。
提取特征 X（包括 SO2、CO、NO2 和 O3）和目标变量 Y（PM2.5）。

划分训练集和测试集：

使用 train_test_split 函数将数据集划分为训练集和测试集，其中训练集占70%。

模型训练与评估：

针对两种不同的激活函数（ReLU 和 Logistic）进行循环：
创建 MLPRegressor 模型，并在训练集上拟合。
使用训练好的模型预测测试集上的结果，计算预测值与真实值之间的 R² 分数。
绘制每种激活函数下的损失曲线 (NeuNet.loss_curve_)，标注测试集的 R² 分数。

绘制损失曲线：

将两种激活函数的损失曲线以及一个额外配置的多层神经网络（四层网络）的损失曲线绘制在同一图中。
添加图例、标题、坐标轴标签，并通过 plt.savefig 将图形保存为文件。

通过这段代码，可以直观地比较不同激活函数在多层感知机模型中的性能表现，帮助选择最适合处理北京市空气质量数据的模型配置和参数设置。

#本章需导入的模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pylab import *
import matplotlib.cm as cm
import warnings
warnings.filterwarnings(action = 'ignore')
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.metrics import zero_one_loss,r2_score,mean_squared_error
import sklearn.neural_network as net

data=pd.read_excel('北京市空气质量数据.xlsx')
data=data.replace(0,np.NaN)
data=data.dropna()
data=data.loc[(data['PM2.5']<=200) & (data['SO2']<=20)]
X=data[['SO2','CO','NO2','O3']]
Y=data['PM2.5']
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.70, random_state=123)

acts=['relu','logistic']
lts=['-','-.']
for lt,act in zip(lts,acts):
    NeuNet=net.MLPRegressor(activation=act,random_state=123,hidden_layer_sizes=(100,))
    NeuNet.fit(X_train,Y_train)
    Y_pred=NeuNet.predict(X_test)
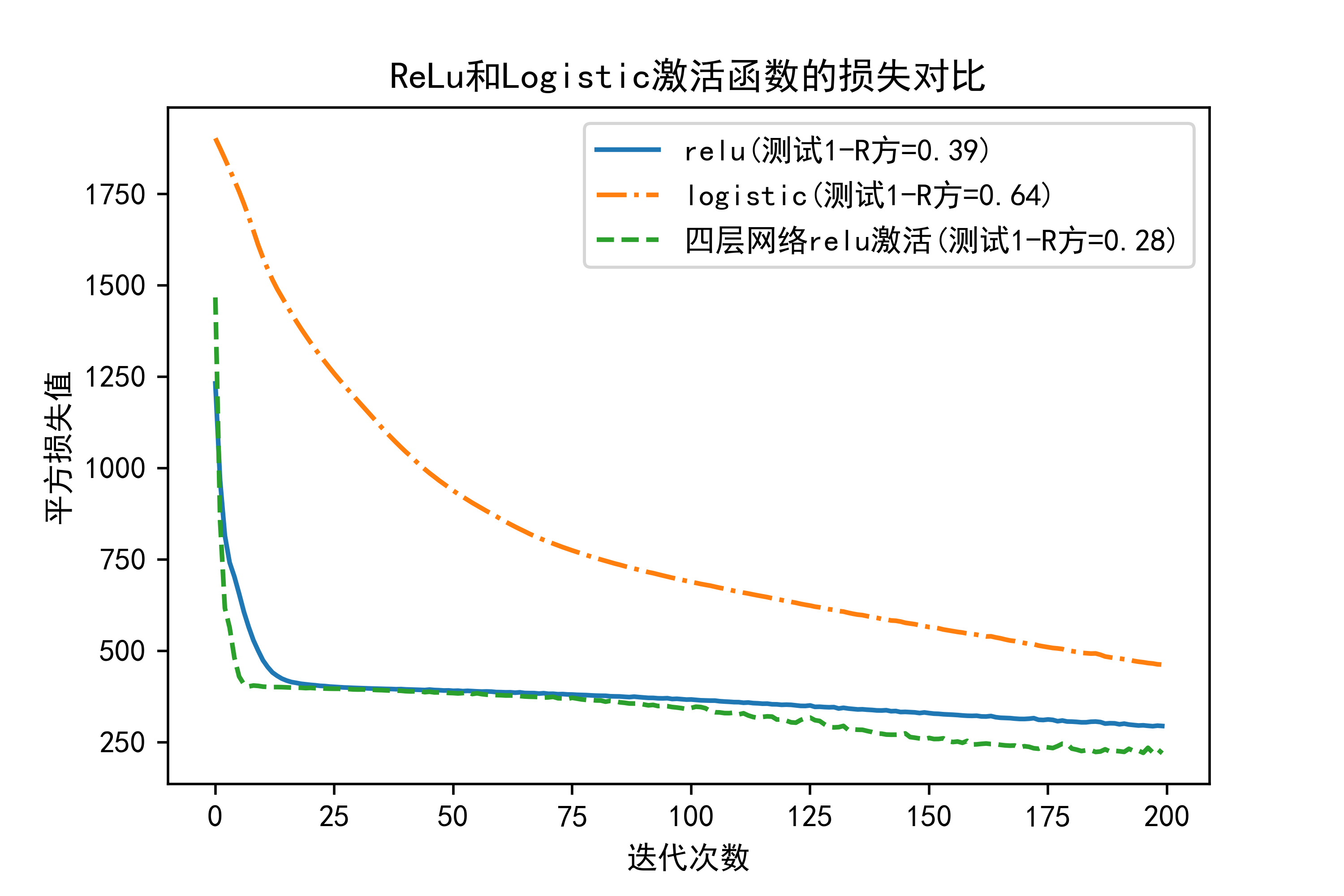
    plt.plot(NeuNet.loss_curve_,label=act+"(测试1-R方=%.2f)"%(1-r2_score(Y_test,Y_pred)),linestyle=lt)
NeuNet = net.MLPRegressor()
NeuNet=net.MLPRegressor(activation='relu',random_state=123,hidden_layer_sizes=(100,50))
NeuNet.fit(X_train,Y_train)
Y_pred=NeuNet.predict(X_test)
plt.plot(NeuNet.loss_curve_,label="四层网络relu激活(测试1-R方=%.2f)"%(1-r2_score(Y_test,Y_pred)),linestyle='--')
plt.legend()
plt.title("ReLu和Logistic激活函数的损失对比")
plt.xlabel("迭代次数")
plt.ylabel("平方损失值")
plt.savefig("../4.png", dpi=500)

运行结果如下图所示：