[机器学习算法]线性回归

news2024/11/24 9:35:47

1. 理解基本概念

在开始学习线性回归之前，确保理解以下基本概念：

自变量（特征）：用来预测因变量（目标）的输入变量。
因变量（目标）：需要预测的输出变量。
回归系数：线性回归模型中每个特征对应的权重。
残差：预测值与真实值之间的差异。

这些概念构成了理解线性回归模型的基础。

2. 学习算法原理

学习线性回归模型的原理涉及以下几个重要方面：

模型表达式：线性回归模型假设因变量与自变量之间是线性关系，表达为：
y=β0+β1x1+β2x2+...+βnxn+ϵ
其中，y 是因变量，x1,x2,...,xn 是自变量，β0,β1,β2,...,βn 是回归系数，ϵ是误差项即残差。

模型训练：通过最小化残差的平方和来求解最优的回归系数，通常使用最小二乘法来实现。

3. 掌握实现步骤

实现线性回归模型的步骤包括：

数据准备：准备包含自变量和因变量的数据集。
模型训练：使用训练数据拟合线性回归模型，估计回归系数。
预测：使用训练好的模型对新的自变量数据进行预测，得到预测值。

在Python中，可以使用Scikit-learn库来实现线性回归，具体步骤如下：

from sklearn.linear_model import LinearRegression

# 准备数据
X_train = ...  # 训练集特征
y_train = ...  # 训练集目标
X_test = ...   # 测试集特征

# 创建线性回归模型
model = LinearRegression()

# 训练模型
model.fit(X_train, y_train)

# 进行预测
y_pred = model.predict(X_test)

4. 研究模型评估

评估线性回归模型的性能是理解其有效性的关键。常用的评估指标包括：

均方误差（Mean Squared Error，MSE）：预测值与真实值之间的平方差的平均值。
决定系数（Coefficient of Determination，R²分数）：表示模型能够解释的方差比例，介于0到1之间，越接近1表示模型拟合得越好。

from sklearn.metrics import mean_squared_error, r2_score

# 计算MSE
mse = mean_squared_error(y_true, y_pred)

# 计算R²分数
r2 = r2_score(y_true, y_pred)

5. 探索模型改进

为了提升线性回归模型的性能，可以考虑以下改进方法：

特征选择：选择最相关的特征来提高模型的预测能力。以房屋价格预测问题为例，房屋的面积 x1 和卧室数量 x2 作为特征。
正则化：如岭回归（Ridge Regression）和Lasso回归（Lasso Regression），用于控制模型复杂度，防止过拟合（即模型在训练数据上表现很好，但在测试数据或实际应用中表现不佳）。
岭回归：在普通最小二乘法的基础上，添加一个正则化项，该项是模型所有参数的平方和乘以一个正则化参数 α。正则化项强制要求模型的系数尽可能小，以减少模型的复杂度。
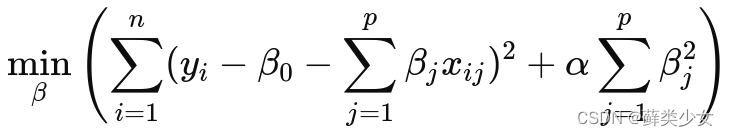其中：
yi 是观测值，
β0 是截距项，
βj 是自变量 xj 的系数，
xij 是第 i 个观测中第 j 个自变量的值，
α 是正则化参数。

Lasso回归：与岭回归类似，但使用的是模型参数的绝对值之和乘以 α。Lasso 回归不仅可以限制系数的大小，还可以将某些不重要的特征的系数缩小甚至置零，从而实现了自动的特征选择。
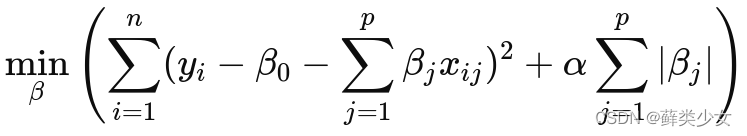
处理异常值和多重共线性：清理数据以及使用技术手段处理数据中的异常值和特征之间的相关性。