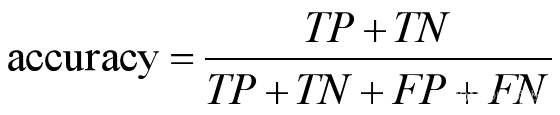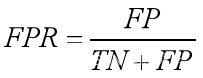一、概念
1.回归就是用一条曲线对数据点进行拟合,该曲线称为最佳拟合曲线,这个拟合过程称为回归。
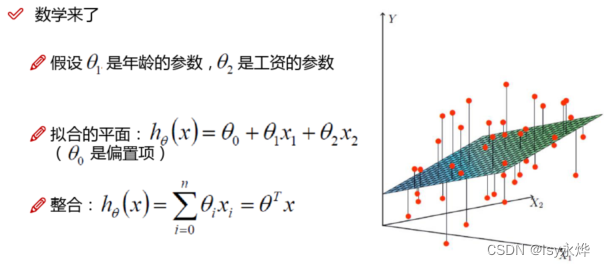
2.一个自变量 叫 一元线性回归,大于一个自变量 叫 多元线性回归。
(1)多元回归:两个x,一个y
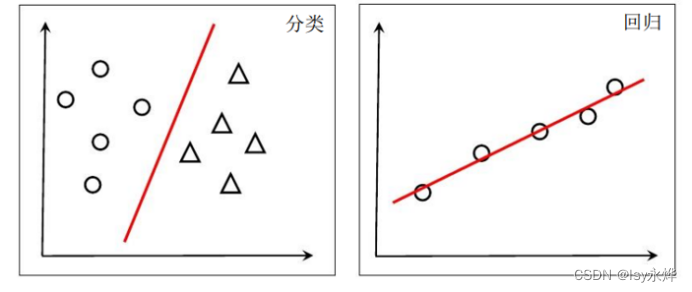
3.这里讲一下线性模型,在二维上就是那根线叫线性模型,他可以用作分类,也可以用作回归:
4. 公式:
(1)准确的说是求 右边的欧米伽和b(用最小二乘法 或者 梯度下降法 求解)。
(2)优化目标:让 【(预测值与真实值之间的欧式距离,下一章)之和】 最小。
预测值就是通过我们用方法推测出的一个点。
真实值就是实际存在的原来样本的一个点,或者说是预测出来本应该是这个点。
5.广义线性模型:
你可以把y替换成lny,原理就跟高中数学里面学的,两边同时取e,最后式子其实是没变化的,这里原理懂了秒懂,不懂得应该也不考无所谓。
6.对率回归 是分类学习算法。其衍生出来的逻辑回归虽然名字中有“回归”,但其主要用途是解决分类问题,特别是二分类问题。
7.梯度下降法简单来说就是一点点求要求的那条直线。
8.人为设置的,而非用来学习的参数,所以叫做超参数。
9.最大熵模型
现实中,不加约束的事物都会朝着“熵增”(不确定,混乱)的方向发展,
当随机变量呈均匀分布时,熵值最大。
最大熵模型就是认为在满足所有约束条件下,熵最大最好(即该情况下数据随机分布,此时最随机,最混乱)。
OK,上面的都不是重点,重点来了:
混淆矩阵
1.基础值缩写:
(1)TN(True negative,真阴率):真0
(2)FN(False nagative,假阴率):假0,即被预测错误的1
(3)TP(True positive,真阳率):真1
(4)FP(False positive,假阳率):假1,即被预测错误的0
2.准确率:表示预测正确的结果占总样本的百分比。
3.精确率(查准率):表示在被预测为正的样本中实际为正的样本的概率。意思就是在预测为正样本的结果中,有多少把握可以预测正确,即不要求对的数量,只要求对的精度/正确率。
4.召回率(查全率):表示在实际为正的样本中被预测为正样本的概率。即是不是所有的1全被找出来了,即要求预测对的数量,但是精度就不保证了。
5.PR曲线:以精确率P为纵坐标,以召回率R为横坐标做出的曲线(竖P横R)。
(1)置信度:(P,R)这样一个点就是置信度
(2)置信度阈值:就是设置一个y轴(P)的值,然后上面的是正例,下面的是负例(上正下负),就是画一条横着的线。
(3)图形:
6.ROC曲线:横轴是假阳率(FPR) 纵轴是真阳率(TPR)
(1)假阳率:
(2)真阳率,就是召回率R:
(3)图形:
(4)x越往右,则表示猜错的正例越来越多,y越往上,则表示猜对的正例越来越多,(1,1)表示此时预测样本全为正例。
二、习题
单选题
7. 逻辑回归模型解决( B)问题
A、回归 B、分类 C、聚类 D、推理
多选题
7. 混淆矩阵大多数评价指标的基础,以下哪些数据它主要包括的信息(ABCD )
A、TN B、TP C、FP D、FN
判断题
6. 逻辑回归是一种广义线性回归,通过回归对数几率的方式将线性回归应用于分类任务。(T)
7. 信息论中,熵可以度量随机变量的不确定性。现实世界中,不加约束的事物都会朝着“熵增”的方向发展,也就是向不确定性增加的方向发展。( T)
8. 准确率可以判断总的正确率,在样本不平衡的情况下,也能作为很好的指标来衡量结果。(F)