1、原理及流程
自适应线性预测是一种基于递归最小二乘法(Recursive Least Squares, RLS)的线性预测方法,用于自适应地估计线性系统的参数。下面是自适应线性预测的原理和流程:
原理: 自适应线性预测的核心思想是通过不断地观察系统输出和实际输出之间的差异,即残差,来调整预测模型的参数,使预测误差最小化。该方法采用递归方式更新参数,适应系统的变化。
流程:
-
初始化:首先,初始化预测模型的参数和协方差矩阵。
-
预测输出:将输入信号送入预测模型中,预测系统的输出。
-
残差计算:计算系统的输出与实际输出之间的残差,即预测误差。
-
参数更新:通过递归最小二乘法来更新预测模型的参数,使残差的平方和最小化。更新过程包括以下步骤:
- 计算增益矩阵:根据协方差矩阵和输入信号计算增益矩阵。
- 更新权值向量:使用增益矩阵和残差来逐步更新预测模型的权值向量。
- 更新协方差矩阵:根据增益矩阵来逐步更新协方差矩阵。
-
输出预测:根据更新后的模型参数,进行下一时刻的输出预测。
-
循环迭代:继续以上步骤,不断观察输出与实际输出的残差,更新模型参数,以适应系统的变化。
通过以上流程,自适应线性预测方法可以动态地调整预测模型的参数,以实现对系统的准确估计和预测。这种方法适用于需要实时调整模型的情况,例如信号处理、通信系统等领域。
2、自适应线性预测问题说明
说明:在给定当前值和最后四个值的情况下,预测信号中的下一个值。
自适应线性预测是一种用于估计线性系统参数的方法,其主要应用领域包括实时信号处理、通信系统、自适应滤波器等。以下是关于自适应线性预测问题的一些说明:
-
动态环境下的参数估计:自适应线性预测适用于需要动态调整模型参数的场景。在许多实时应用中,系统参数可能随时间变化,通过不断观察系统输出和实际输出之间的残差,自适应线性预测可以实现对参数的实时更新。
-
非稳态信号处理:自适应线性预测常用于处理非稳态信号,即信号统计特性随时间变化的情况。通过不断迭代的方式更新模型参数,可以更好地适应信号的变化,提高模型的性能。
-
降低噪声干扰:在通信系统和信号处理领域,常常会受到噪声和干扰的影响,自适应线性预测可以帮助降低噪声对系统性能的影响,实现更准确的信号预测和恢复。
-
自适应滤波器:自适应线性预测在自适应滤波器中具有重要应用。通过实时调整滤波器的权值系数,可以实现对输入信号的实时滤波和噪声抑制。
-
在线学习:与批量学习相比,自适应线性预测是一种在线学习方法,能够实时更新模型参数而无需保存大量历史数据。这使得自适应线性预测在处理长时间序列和实时数据时具有优势。
总的来说,自适应线性预测是一种强大的方法,适用于需要实时调整模型参数、处理动态环境和抑制噪声干扰的应用场景。通过不断迭代更新模型参数,自适应线性预测能够提高系统的性能和适应能力。
3、定义波形
说明1
两个时间段定义为 0 到 6 秒,步长为 1/40 秒。
代码
time1 = 0:0.025:4; % 0到4秒
time2 = 4.025:0.025:6; % 4到6秒
time = [time1 time2]; % 0到6秒说明2
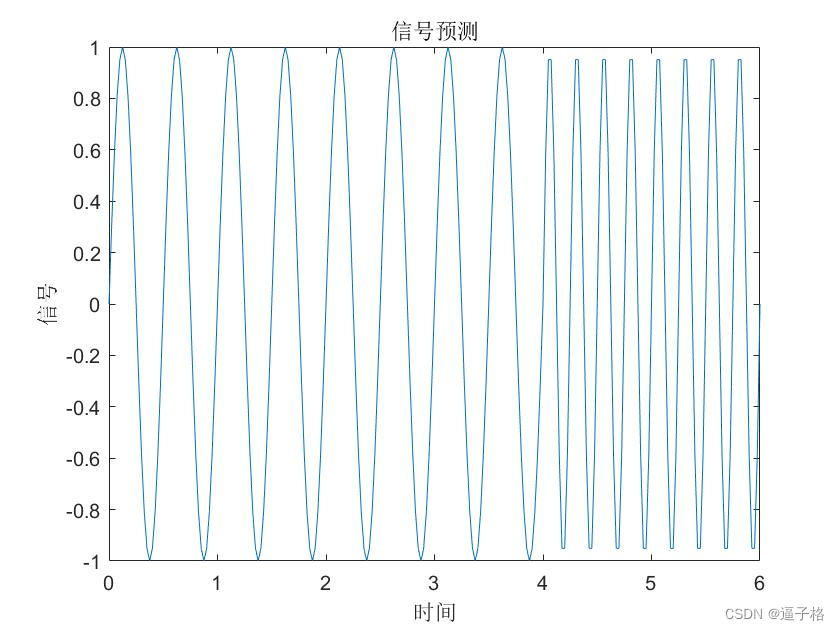
信号从一个频率开始,然后转换到另一个频率。
代码
signal = [sin(time1*4*pi) sin(time2*8*pi)];
figure(1)
plot(time,signal)
xlabel('时间');
ylabel('信号');
title('信号预测');试图效果
4、神经网络设置问题
说明1
将信号转换为元胞数组。
代码
signal = con2seq(signal);说明2
使用信号的前五个值作为初始输入延迟状态,其余的值作为输入。
代码
Xi = signal(1:5);
X = signal(6:end);
timex = time(6:end);说明3
目标定义为匹配输入,网络仅使用最后五个值来预测当前输入。
代码
T = signal(6:end);5、创建线性层
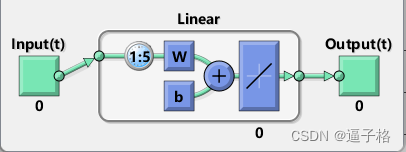
说明
函数 linearlayer 创建一个线性层,该层由一个神经元组成,最后五个输入具有抽头延迟。
代码
net = linearlayer(1:5,0.1);
view(net)视图效果
6、 自适应线性层
说明1
说明:函数 adapt 在输入端对网络进行仿真,同时在每个时间步后调整其权重和偏置,以反映其输出与目标的匹配程度。它返回更新网络、其输出及错误。
代码
[net,Y] = adapt(net,X,T,Xi);说明2
绘制输出信号与目标。
代码
figure(2)
plot(timex,cell2mat(Y),timex,cell2mat(T),'+')
xlabel('时间');
ylabel('输出信号与目标');
title('输出信号与目标');
legend('预测信号','原始信号')试图效果
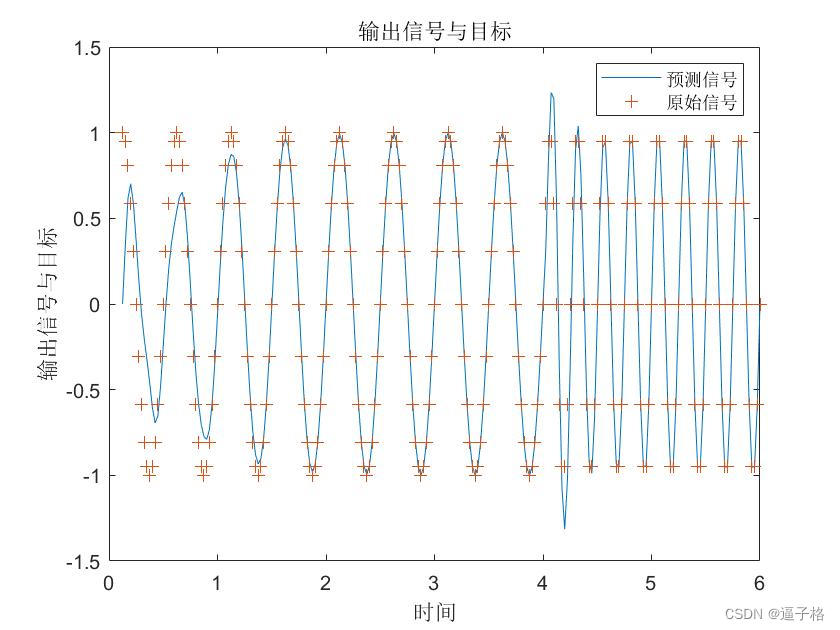
说明3
绘制误差
代码
figure(3)
E = cell2mat(T)-cell2mat(Y);
plot(timex,E,'b')
xlabel('时间');
ylabel('误差');
title('误差信号');视图效果
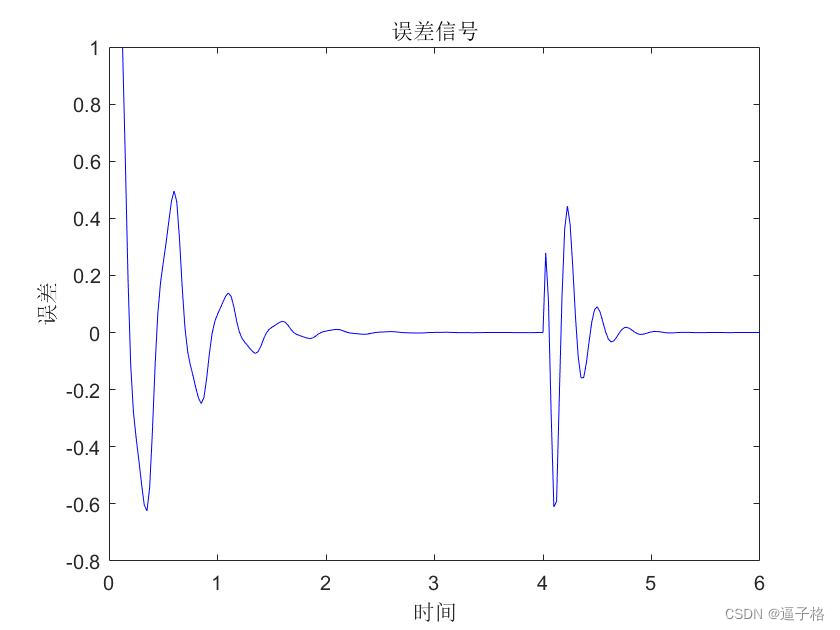
7、总结
在 MATLAB 中实现自适应线性预测通常涉及以下几个步骤:
-
定义输入信号和期望输出:首先,需要定义输入信号和期望输出的数据,通常存储在 MATLAB 的向量或矩阵中。
-
初始化模型参数:初始化自适应线性预测模型的权值向量、协方差矩阵等参数。
-
实现自适应线性预测算法:编写 MATLAB 代码实现自适应线性预测算法的主要步骤,包括计算残差、更新权值向量、更新协方差矩阵等。
-
参数更新和预测输出:在循环中不断执行模型参数的更新和预测输出,直至模型收敛或达到停止条件。
-
性能评估:在模型收敛后,可以评估预测输出与实际输出之间的残差,以及模型的性能表现。
以下是一个简单的伪代码示例,演示了在 MATLAB 中实现自适应线性预测的基本步骤:
% 初始化模型参数
w = zeros(N, 1);
% 初始化权值向量
P = eye(N) * delta;
% 初始化协方差矩阵
lambda = 0.99;
% 设置遗忘因子 % 循环迭代
for i = 1:length(input_signal) x = input_signal(i);
% 获取当前时刻的输入信号
% 预测输出
y_hat = w' * x;
% 计算残差
e = desired_output(i) - y_hat;
% 计算增益矩阵
K = P * x / (lambda + x' * P * x);
% 更新权值向量 w = w + K * e;
% 更新协方差矩阵
P = (P - K * x' * P) / lambda; end需要根据具体的问题场景和模型要求来调整参数和算法细节。这个示例代码演示了一个简单的自适应线性预测算法的框架,实际应用中可能需要根据情况做更多的优化和调整。
8、源代码
%% 自适应线性预测
%说明:在给定当前值和最后四个值的情况下,预测信号中的下一个值。
%% 定义波形
%说明:两个时间段定义为 0 到 6 秒,步长为 1/40 秒。
time1 = 0:0.025:4; % 0到4秒
time2 = 4.025:0.025:6; % 4到6秒
time = [time1 time2]; % 0到6秒
%说明:信号从一个频率开始,然后转换到另一个频率。
signal = [sin(time1*4*pi) sin(time2*8*pi)];
figure(1)
plot(time,signal)
xlabel('时间');
ylabel('信号');
title('信号预测');
%% 神经网络设置问题
%说明:将信号转换为元胞数组。
signal = con2seq(signal);
%说明:使用信号的前五个值作为初始输入延迟状态,其余的值作为输入。
Xi = signal(1:5);
X = signal(6:end);
timex = time(6:end);
%说明:目标定义为匹配输入,网络仅使用最后五个值来预测当前输入。
T = signal(6:end);
%% 创建线性层
%说明:函数 linearlayer 创建一个线性层,该层由一个神经元组成,最后五个输入具有抽头延迟。
net = linearlayer(1:5,0.1);
view(net)
%% 自适应线性层
%说明:函数 adapt 在输入端对网络进行仿真,同时在每个时间步后调整其权重和偏置,以反映其输出与目标的匹配程度。它返回更新网络、其输出及错误。
[net,Y] = adapt(net,X,T,Xi);
%绘制输出信号与目标。
figure(2)
plot(timex,cell2mat(Y),timex,cell2mat(T),'+')
xlabel('时间');
ylabel('输出信号与目标');
title('输出信号与目标');
legend('预测信号','原始信号')
%绘制误差
figure(3)
E = cell2mat(T)-cell2mat(Y);
plot(timex,E,'b')
xlabel('时间');
ylabel('误差');
title('误差信号');