基于密度的LOF异常值检测可见上篇文章。以下介绍基于预测的异常值检测:
1.基于预测的异常值检测方法
基于预测的异常值检测方法,特别是结合线性回归和ARIMA(自回归积分滑动平均模型)模型,是数据分析中常用的技术。这些方法的核心思想是利用模型的预测能力来识别与预期值偏差较大的数据点,这些点往往被视为异常值。以下是对这两种方法及其异常值检测的详细介绍:
2.基于线性回归异常值检测
2.1 线性回归异常检测介绍
线性回归模型:线性回归是统计学中的一个基本模型,用于通过一系列自变量(特征)来预测一个因变量(目标变量)。在线性回归模型中,异常值通常被定义为那些与模型预测值存在显著偏差的数据点。
以标准化残差为依据衡量异常值:为了更好地评估残差的大小,可以将其标准化(即将残差除以其标准差)。标准化残差大于某个阈值(如2或3)的数据点被视为异常值。本文使用正态分布生成随机数据,所以阈值设为3。
2.2 线性回归案例代码
接下来利用matlab实例代码介绍:
| % 清除命令窗口 clc % 清除工作空间中的所有变量 clear % 创建示例数据 % 设置随机数生成器的种子为'default',以便得到可重复的结果 rng('default'); % 定义数据点的数量 n = 100; % 创建一个从1到n的列向量作为自变量x x = (1:n)'; % 创建一个因变量y,它是自变量x的两倍加5,再加上一些随机的正态分布噪声 % randn(n,1)*10 生成一个n行1列的矩阵,其元素来自均值为0、标准差为10的正态分布 y = 2*x + 5 + randn(n,1)*10; % 插入一些异常值 % 将第20、50、80个数据点的y值增加50,使其成为异常值 y([20, 50, 80]) = y([20, 50, 80]) + 50; % 绘制原始数据 figure; % 创建一个新的图形窗口 scatter(x, y, 'filled'); % 使用散点图绘制原始数据,'filled'表示填充标记 title('原始数据'); % 设置图形标题 xlabel('X'); % 设置x轴标签 ylabel('Y'); % 设置y轴标签 % 线性回归模型拟合 % 使用fitlm函数拟合线性模型 mdl = fitlm(x, y); % 预测值 % 使用predict函数基于拟合的模型预测y值 y_pred = predict(mdl, x); % 计算残差 % 残差是观测值与预测值之间的差异 residuals = y - y_pred; % 设置残差的阈值,超过该阈值的点被视为异常值 % 这里使用残差的3倍标准差作为阈值 threshold = 3 * std(residuals); isAnomaly = abs(residuals) > threshold;% 0为正常值,1为异常值 % 创建一个逻辑数组isAnomaly,如果残差的绝对值大于阈值,则对应位置为true % 绘制结果 figure; % 创建一个新的图形窗口 hold on; % 保持当前图形,以便在同一图形上添加更多内容 scatter(x, y, 'filled'); % 绘制原始数据 plot(x, y_pred, 'r', 'LineWidth', 1.5); % 绘制预测值的线,使用红色并设置线宽为2 scatter(x(isAnomaly), y(isAnomaly), 'filled', 'r'); % 绘制异常值,使用红色填充标记 title('线性回归异常值检测'); % 设置图形标题 xlabel('X'); % 设置x轴标签 ylabel('Y'); % 设置y轴标签 legend('原始数据', '预测值', '异常值'); % 添加图例 hold off; % 释放当前图形,以便可以添加新的图形 |
最终,matlab输出的异常点为20、50、80,线性回归异常值检测图如下:
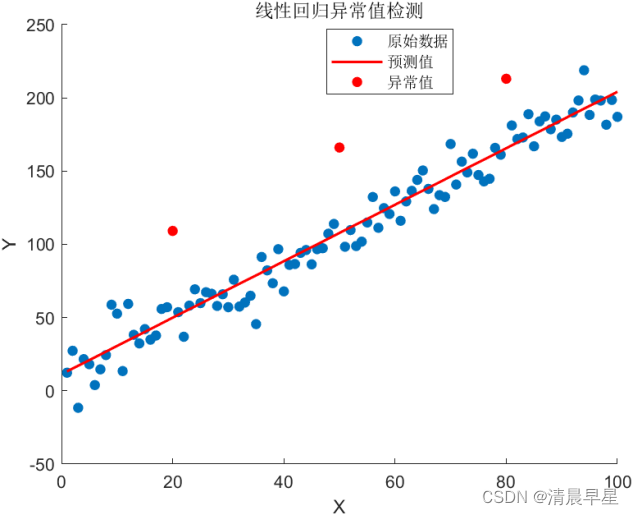
3.基于ARIMA异常值检测
3.1 ARIMA异常检测介绍
ARIMA模型:ARIMA模型是一种用于时间序列数据预测的统计模型,它由自回归(AR)、差分(I)和移动平均(MA)三个部分组成。ARIMA模型通过捕捉时间序列数据中的自相关性和趋势来进行预测。
以预测误差为依据衡量异常值:使用ARIMA模型对时间序列数据进行预测后,可以计算每个数据点的预测误差(即实际值与预测值之差)。与线性回归类似,预测误差远大于其他数据点的预测误差的数据点被视为异常值。标准化残差大于某个阈值(如2或3)的数据点被视为异常值。本文使用正态分布生成随机数据,所以阈值设为3。
3.2 ARIMA案例代码
接下来利用matlab实例代码介绍:
| clc clear % 创建时间序列数据 rng('default'); % 固定随机数生成器种子 n = 100; y = cumsum(randn(n,1)); % 随机游走时间序列 % 插入一些异常值 y([20, 50, 80]) = y([20, 50, 80]) + 20; % 绘制原始数据 figure; plot(y); title('原始时间序列数据'); xlabel('时间'); ylabel('值'); % 自动选择最佳的 p, d, q 组合 bestAIC = Inf; bestModel = []; bestPQD = [0, 0, 0]; maxP = 3; % 最大 p 值 maxD = 2; % 最大 d 值 maxQ = 3; % 最大 q 值 for p = 0:maxP for d = 0:maxD for q = 0:maxQ try % 拟合 ARIMA 模型 mdl = arima(p, d, q); fit = estimate(mdl, y, 'Display', 'off'); % 计算 AIC 值 aic = aicbic(logL, numParams); if aic < bestAIC bestAIC = aic; bestModel = fit; bestPQD = [p, d, q]; end catch % 如果模型估计失败,跳过 continue end end end end fprintf('最佳 ARIMA 模型: p = %d, d = %d, q = %d\n', bestPQD(1), bestPQD(2), bestPQD(3)); % 拟合 ARIMA 模型 mdl = arima(bestPQD(1),bestPQD(2),bestPQD(3)); % 这里选择最优ARIMA(p,d,q) 模型 fit = estimate(mdl, y); % 预测值 [y_pred, y_pred_mse] = forecast(fit, n, 'Y0', y); % 计算残差 residuals = y - y_pred; % 设置残差的阈值,超过该阈值的点被视为异常值 threshold = 3 * sqrt(y_pred_mse); isAnomaly = abs(residuals) > threshold; % 绘制结果 figure; hold on; plot(y, 'b'); % 原始数据 plot(y_pred, 'r', 'LineWidth', 1.5); % 预测值 plot(find(isAnomaly), y(isAnomaly), 'r*', 'MarkerSize', 5); % 异常值 title('ARIMA 异常值检测'); xlabel('时间'); ylabel('值'); legend('原始数据', '预测值', '异常值'); hold off; |
最终,matlab输出的异常点为20、50、80,ARIMA异常值检测图如下:

其中,ARIMA(0,0,0)模型参数如下图,但是实际情况中p=d=q=0一般是不存在的,此处是作者随机生成的正态数据的结果。

4.4 基于预测的优缺点
优点:
简单易懂:线性回归模型基于简单的数学公式,易于理解和实现。
可解释性强:模型的参数(系数)具有明确的物理含义,能够清晰地解释自变量对因变量的影响程度。
计算效率高:线性回归算法的计算量较小,适用于大规模数据集的训练和预测。
缺点:
对非线性关系拟合能力有限:线性回归模型只能捕捉变量之间的线性关系,对于非线性关系的数据拟合效果较差。
对异常值敏感:由于最小二乘法的目标是最小化误差平方和,线性回归模型对异常值(离群点)非常敏感,一个异常值可能会对模型的结果产生较大的影响。
对多重共线性敏感:当自变量之间存在高度相关性(多重共线性)时,线性回归模型的参数估计可能不准确,模型的表现可能不稳定。
基于预测的异常值检测具有其独特的优缺点,以下是详细的介绍:
优点
广泛适用性:这种方法不依赖于大量的先验知识,适用于各种数据类型。无论是数值型数据、时间序列数据还是其他复杂类型的数据,只要能够建立相应的预测模型,就可以进行异常值检测。
高准确性:基于机器学习的预测方法,如使用ARIMA模型或深度学习模型,能够更好地挖掘数据的内在特征,提高异常值检测的准确性。这些方法通过学习和训练大量数据,能够识别出复杂模式中的异常点。
缺点
误报和漏报:在某些情况下,基于预测的方法可能会出现误报(将正常数据误判为异常)或漏报(未能检测出真正的异常数据)。这可能是由于模型的预测误差、数据噪声或异常值的复杂性导致的。
计算复杂性和资源需求:某些基于预测的方法,尤其是基于机器学习的方法,需要大量的计算复杂性和计算资源来进行训练和预测。这可能会增加实施成本和时间成本。
对高维数据的挑战:对于高维数据,基于距离和密度的方法可能会出现空间分布稀疏等问题,导致异常值检测的准确性下降。
模型选择和参数调整:选择合适的预测模型和调整模型的参数是一个挑战。不同的数据和问题可能需要不同的模型和参数设置,这需要一定的专业知识和经验。