python数据分析--- ch12-13 python参数估计与假设检验
- 1. Ch12--python 参数估计
- 1.1 参数估计与置信区间的含义及函数版
- 1.1.1 参数估计与置信区间的含义
- 1.1.2 参数估计函数版
- 1.1.3 参数估计函数版
- 1.2 Python单正态总体均值区间估计
- 1.3 Python单正态总体方差区间估计
- 1.4 Python双正态总体均值差区间估计
- 1.5 两方差都未知时两均值差的置信区间
- 1.6 Python双正态总体方差比区间估计
- 2. Ch13--python 假设检验
- 2.1 Python单个样本t检验
- 2.2 Python两个独立样本t检验
- 2.3 Python配对样本t检验
- 2.4 两独立样本 vs 配对样本
- 2.4.1 两个独立样本t检验
- 2.4.2 配对样本t检验
- 2.4.3 总结
- 2.5 Python单样本方差假设检验
- 2.6 Python双样本方差假设检验
1. Ch12–python 参数估计
1.1 参数估计与置信区间的含义及函数版
1.1.1 参数估计与置信区间的含义
参数估计和置信区间是统计学中的两个重要概念,它们在数据分析和推断统计中扮演着关键角色。下面分别解释这两个概念:
1.参数估计(Parameter Estimation)
参数估计是指使用样本数据来估计总体参数的过程。在统计学中,总体参数是指描述整个数据集的特征值,如总体均值(μ)、总体方差(σ²)等。由于我们通常无法获得整个总体的数据,因此需要从总体中抽取一部分样本,然后通过样本数据来推断总体参数。
参数估计有两种主要类型:
-
点估计(Point Estimation):这是最基本的估计方法,它提供了一个单一的数值作为总体参数的估计。例如,样本均值((\bar{x}))通常被用作总体均值(μ)的点估计。
x ˉ = ∑ i = 1 n x i n \bar{x} = \frac{\sum_{i=1}^{n} x_i}{n} xˉ=n∑i=1nxi
其中, x ˉ \bar{x} xˉ表示均值, x i x_i xi表示第 𝑖个数值,而 𝑛是数值的总数,即样本数。 -
区间估计(Interval Estimation):这种方法提供了一个数值范围,这个范围以一定的概率包含总体参数。区间估计通常比点估计提供更多信息,因为它包含了不确定性的度量。
例12-1:对某个篮球运动员记录其在某一次比赛中投篮命中与否,观测数据如下:
1 1 0 1 0 0 1 0 1 1 1 0 1 1 0 1
0 0 1 0 1 0 1 0 0 1 1 0 1 1 0 1
编写Python程序估计这个篮球运动员投篮的成败比。
import numpy as np
x=[1,1,0,1,0,0,1,0,1,1,1,0,1,1,0,1,0,0,1,0,1,0,1,0,0,1,1,0,1,1,0,1]
theta=np.mean(x)
h=theta/(1-theta)
print ('h=',round(h,4))
output
h= 1.2857
2.置信区间(Confidence Interval)
置信区间是区间估计的一种形式,它表示我们对总体参数估计的可信程度。一个置信区间通常表示为:估计值 ± 误差范围,其中误差范围被称为置信区间的“半宽”。数学表达式如下:
置信区间 = x ^ ± z α / 2 × S E ( x ^ ) \text{置信区间} = \hat{x} \pm z_{\alpha/2} \times SE(\hat{x}) 置信区间=x^±zα/2×SE(x^)
其中,$ z_{\alpha/2} $ 是标准正态分布的 $ \alpha/2 $ 分位数,$ SE(\hat{x})$ 是
x
^
\hat{x}
x^ 的标准误差。
置信区间的关键组成部分包括:
-
置信水平(Confidence Level):这是一个百分比,表示我们有多大的信心认为置信区间包含了总体参数。常见的置信水平有90%、95%和99%。
-
置信区间的宽度:这取决于样本大小、样本变异性以及所选的置信水平。较大的样本大小和较低的变异性通常会导致更窄的置信区间。
-
总体参数:置信区间试图估计的总体特征,如均值、比例或差异。
例如,如果我们说“总体均值的95%置信区间是20到30”,这意味着我们有95%的信心认为总体均值位于20到30的范围内,基于我们从样本中得到的信息。
例12-2:假设一位投资分析师从股权基金中选取了一个随机样本,并计算出了平均的夏普比率。样本的容量为100,并且平均的夏普比率为0.45。该样本具有的标准差为0.300。利用一个基于标准正态分布的临界值,编写python程序计算并解释所有股权基金总体均值的90%置信区间。( z 0.05 = 1.65 z_{0.05}=1.65 z0.05=1.65)
import numpy as np
up=0.45+1.65*(0.300/np.sqrt(100))
low=0.45-1.65*(0.300/np.sqrt(100))
print(f"置信区间为:[{round(low,4)},{round(up,4)}]")
output
置信区间为:[0.4005,0.4995]
1.1.2 参数估计函数版
import scipy.stats as ss
import math
#confidence_interval
def norm1_ci_4mean(n, x_bar, alpha, sigma=None, s=None):
"""
计算单正态总体均值的置信区间。
参数:
n : int
样本大小。
x_bar : float
样本均值。
alpha : float
置信水平,例如0.05表示95%置信区间。
sigma : float, optional
总体标准差,如果为None,则假定总体方差未知。
s : float, optional
样本标准差,如果为None且sigma也为None,则假定总体方差未知。
返回:
tuple
均值的置信区间下限和上限。
"""
# 计算置信区间的临界值
if sigma is None and s is not None:
if n<30:
# 总体方差未知,使用t分布
critical = ss.t.ppf(1 - alpha / 2, df=n - 1)
else:
critical = ss.norm.ppf(1 - alpha / 2)
elif sigma is not None and s is None:
# 总体方差已知,使用正态分布
critical = ss.norm.ppf(1 - alpha / 2)
else:
raise ValueError("参数sigma和s不能同时为None或非None。")
print(critical)
# 计算置信区间
if sigma is None:
# 使用样本标准差和t分布
margin_of_error = critical * (s / math.sqrt(n))
else:
# 使用总体标准差和正态分布
margin_of_error = critical * (sigma / math.sqrt(n))
low_bound = x_bar - margin_of_error
up_bound = x_bar + margin_of_error
return [round(low_bound, 4), round(up_bound, 4)]
def norm1_ci_4var(n, var, alpha):
"""
计算单正态总体方差的置信区间。
参数:
n : int
样本大小。
var : float
样本方差。
alpha : float
置信水平,例如0.05表示95%置信区间。
返回:
list
方差的置信区间下限和上限。
"""
# 计算置信区间的临界值
low_critical = ss.chi2.ppf(1 - alpha/2, df=n - 1)
up_critical = ss.chi2.ppf(alpha/2, df=n - 1)
low_bound = (n-1)*var/low_critical
up_bound = (n-1)*var/up_critical
return [round(low_bound, 4), round(up_bound, 4)]
def norm2_ci_4difference_mean(x1_bar,x2_bar,n1,n2,alpha,s1_2=None,s2_2=None,sigma1_2=None,sigma2_2=None):
"""
计算两个独立正态总体均值之差的置信区间。
参数:
mu1 : float
第一个样本的均值。
s1 : float
第一个样本的标准差。
n1 : int
第一个样本的大小。
mu1 : float
第二个样本的均值。
s2 : float
第二个样本的标准差。
n2 : int
第二个样本的大小。
alpha : float
置信水平,例如0.05表示95%置信区间。
equal_var : bool, optional
如果为True,则假定两个总体方差相等,使用z统计量;如果为False,则假定方差不相等,使用t统计量。
返回:
list
均值差值的置信区间下限和上限。
"""
critical_value = 0
std_error = 0
# 计算均值差值的标准误差
if sigma1_2 is not None and sigma2_2 is not None:#两总体方差已知
std_error = math.sqrt(sigma1_2 / n1 + sigma2_2 / n2)
critical_value = ss.norm.ppf(1 - alpha/2)
if s1_2 is not None and s2_2 is not None:#两总体方差未知但相等
s_2 = ((n1-1)*s1_2 + (n2-1)*s2_2)/((n1-1)+(n2-1))
std_error = math.sqrt((1/n1 + 1/n2)*s_2)
critical_value = ss.t.ppf(1 - alpha/2,df = n1+n2-2)
# 计算置信区间
margin_of_error = critical_value * std_error
low_bound = x1_bar-x2_bar - margin_of_error
up_bound = x1_bar-x2_bar + margin_of_error
return [round(low_bound, 4), round(up_bound, 4)]
def norm2_ci_4var(s1_2,s2_2,n1,n2,alpha):
"""
计算两个独立正态总体均值之差的置信区间。
参数:
s1 : float
第一个样本的标准差。
n1 : int
第一个样本的大小。
s2 : float
第二个样本的标准差。
n2 : int
第二个样本的大小。
alpha : float
置信水平,例如0.05表示95%置信区间。
返回:
list
均值差值的置信区间下限和上限。
"""
low_critical_value = 1/ss.f.ppf(1-alpha/2, n1-1, n2-1)
up_critical_value = 1/ss.f.ppf(alpha/2, n1-1, n2-1)
# 计算均值差值的标准误差
low_bound = s1_2/s2_2*low_critical_value
up_bound = s1_2/s2_2*up_critical_value
return [round(low_bound, 4), round(up_bound, 4)]
# 示例使用
n = 100
x_bar = 0.45
alpha = 0.1
sigma = None # 假设总体方差未知
s = 0.3 # 样本标准差
# 调用函数
ci = norm1_confidence_interval_4mean(n, x_bar, alpha, sigma, s)
print(f"{(1-alpha)*100}%置信区间为:{ci}")
output
90.0%置信区间为:[0.4007, 0.4993]
1.1.3 参数估计函数版
from scipy import stats
import math
from typing import Tuple, Optional
class ParameterEstimation:
@staticmethod
def norm1_ci_for_mean(n: int, x_bar: float, alpha: float, sigma: Optional[float] = None, s: Optional[float] = None) -> Tuple[float, float]:
"""
计算单正态总体均值的置信区间。
"""
if sigma is not None and s is not None:
raise ValueError("Provide either sigma (known population standard deviation) or s (sample standard deviation), not both.")
critical_value = stats.t.ppf(1 - alpha / 2, df=n - 1) if s is not None else stats.norm.ppf(1 - alpha / 2)
margin_of_error = critical_value * (s / math.sqrt(n) if s is not None else sigma)
return (round(x_bar - margin_of_error, 4), round(x_bar + margin_of_error, 4))
@staticmethod
def norm1_ci_for_var(n: int, sample_var: float, alpha: float) -> Tuple[float, float]:
"""
计算单正态总体方差的置信区间。
"""
critical_value_low = stats.chi2.ppf(1 - alpha / 2, df=n - 1)
critical_value_high = stats.chi2.ppf(alpha / 2, df=n - 1)
lower_bound = (n - 1) * sample_var / critical_value_low
upper_bound = (n - 1) * sample_var / critical_value_high
return (round(lower_bound, 4), round(upper_bound, 4))
@staticmethod
def norm2_ci_for_difference_of_means(x_bar1: float, x_bar2: float, n1: int, n2: int, alpha: float, s1: Optional[float] = None, s2: Optional[float] = None, sigma1: Optional[float] = None, sigma2: Optional[float] = None) -> Tuple[float, float]:
"""
计算两个独立正态总体均值之差的置信区间。
"""
if (sigma1 is not None and sigma2 is not None) and (s1 is not None and s2 is not None):
raise ValueError("For known population variances, do not provide sample standard deviations.")
std_error = math.sqrt(sigma1 / n1 + sigma2 / n2) if sigma1 is not None and sigma2 is not None else math.sqrt(((n1 - 1) * s1 + (n2 - 1) * s2) / (n1 + n2 - 2))
critical_value = stats.t.ppf(1 - alpha / 2, df=n1 + n2 - 2) if s1 is not None and s2 is not None else stats.norm.ppf(1 - alpha / 2)
margin_of_error = critical_value * std_error
difference = x_bar1 - x_bar2
return (round(difference - margin_of_error, 4), round(difference + margin_of_error, 4))
@staticmethod
def norm2_ci_for_var_ratio(s1: float, s2: float, n1: int, n2: int, alpha: float) -> Tuple[float, float]:
"""
计算两个独立正态总体方差比的置信区间。
"""
critical_value_low = 1 / stats.f.ppf(1 - alpha / 2, dfn=n1 - 1, dfd=n2 - 1)
critical_value_high = 1 / stats.f.ppf(alpha / 2, dfn=n1 - 1, dfd=n2 - 1)
lower_bound = s1 / s2 * critical_value_low
upper_bound = s1 / s2 * critical_value_high
return (round(lower_bound, 4), round(upper_bound, 4))
# 示例使用
try:
ci_mean = ParameterEstimation.norm1_ci_for_mean(n=100, x_bar=50, alpha=0.05, s=5)
print(f"Confidence interval for mean: {ci_mean}")
except ValueError as e:
print(e)
output
Confidence interval for mean: (49.0079, 50.9921)
- 总结
参数估计是使用样本数据来推断总体特征的过程,而置信区间是参数估计的一种形式,它提供了一个数值范围,表示我们对总体参数估计的可信程度。置信区间的宽度和所选的置信水平反映了估计的不确定性。在实际应用中,选择合适的置信水平和理解置信区间的含义对于做出准确的统计推断至关重要。
1.2 Python单正态总体均值区间估计
1.2.1 方差 σ 2 \sigma^2 σ2已知
置信区间 = x ˉ ± Z α 2 σ n = ( x ˉ − Z α 2 σ n , x ˉ + Z 1 − α 2 σ n ) \text{置信区间} = \bar{x} \pm Z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}=(\bar{x} - Z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}},\bar{x} + Z_{1-\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}) 置信区间=xˉ±Z2αnσ=(xˉ−Z2αnσ,xˉ+Z1−2αnσ)
例12-3:某车间生产的滚珠直径X服从正态分布N(u,0.6)。现从某天的产品中抽取6个,测得直径如下(单位:mm):
14.6,15.1,14.9,14.8,15.2,15.1
编写python程序试求置信度为95%的平均直径置信区间。
import numpy as np
import scipy.stats as ss
n = 6; p = 0.025; sigma = np.sqrt(0.6)
x=[14.6,15.1,14.9,14.8,15.2,15.1]
xbar=np.mean(x)
low = xbar - ss.norm.ppf(q = 1 - p) * (sigma / np.sqrt(n))
up = xbar + ss.norm.ppf(q = 1 - p) * (sigma / np.sqrt(n))
print ('low=',round(low,4))
print ('up=',round(up,4))
output
low= 14.3302
up= 15.5698
import numpy as np
n = 6
x=[14.6,15.1,14.9,14.8,15.2,15.1]
x_bar = np.mean(x)
alpha = 0.05
sigma = np.sqrt(0.6) # 总体标准差
s = None # 样本标准差
# 调用函数
ci = norm1_confidence_interval_4mean(n, x_bar, alpha, sigma, s)
print(f"{(1-alpha)*100}%置信区间为:{ci}")
output
1.959963984540054
95.0%置信区间为:[14.3302, 15.5698]
1.2.2 方差 σ 2 \sigma^2 σ2未知
置信区间 = x ˉ ± t α 2 ( n − 1 ) S n = ( x ˉ − t α 2 ( n − 1 ) S n , x ˉ + t 1 − α 2 ( n − 1 ) S n ) \text{置信区间} = \bar{x} \pm t_{\frac{\alpha}{2}}(n-1) \frac{S}{\sqrt{n}}=(\bar{x} - t_{\frac{\alpha}{2}}(n-1) \frac{S}{\sqrt{n}} , \bar{x} + t_{1-\frac{\alpha}{2}}(n-1) \frac{S}{\sqrt{n}}) 置信区间=xˉ±t2α(n−1)nS=(xˉ−t2α(n−1)nS,xˉ+t1−2α(n−1)nS)
例12-4:某糖厂自动包装机装糖,设各包重量服从正态分布N(u, σ 2 \sigma^2 σ2)。 某日开工后测得9包重量为(单位:kg):
99.10,98.7,100.5,101.2,98.10,99.7,99.5,102.1,100.5
编写python程序试求置信度为95%的平均直径置信区间。
import numpy as np
import scipy.stats as ss
from scipy.stats import t
n = 9; p = 0.025; s = np.sqrt(1.47)
x=[99.3,98.7,100.5,101.2,98.3,99.7,99.5,102.1,100.5]
xbar=np.mean(x)
low = xbar - ss.t.ppf(1-p,n-1) * (s / np.sqrt(n))
up = xbar + ss.t.ppf(1-p,n-1) * (s / np.sqrt(n))
print ('low=',round(low,4))
print ('up=',round(up,4))
output
low= 99.0458
up= 100.9097
import numpy as np
x=[99.3,98.7,100.5,101.2,98.3,99.7,99.5,102.1,100.5]
# 调用函数
alpha=0.05
ci = norm1_confidence_interval_4mean(n=9, x_bar=np.mean(x), alpha=0.05, sigma=None, s=np.sqrt(1.47))
print(f"{(1-alpha)*100}%置信区间为:{ci}")
output
2.3060041350333704
95.0%置信区间为:[99.0458, 100.9097]
from scipy import stats
import numpy as np
x=[99.3,98.7,100.5,101.2,98.3,99.7,99.5,102.1,100.5]
stats.t.interval(0.95,len(x)-1,np.mean(x),stats.sem(x))
output
(99.04599342616191, 100.90956212939363)
1.3 Python单正态总体方差区间估计
此时虽然也可以就均值是否已知分两种情况讨论方差的区间估计,但在实际中u已知的情形是极为罕见的,所以只讨论在u未知的情况下,方差 σ 2 \sigma^2 σ2的置信区间。
例12-5 从某车间加工的同类零件中抽取了16件,测得零件的平均长度为12.8厘米,方差为0.0023。假设零件的长度服从正态分布,试求总体方差及标准差的置信区间(置信度为95%)。
from scipy.stats import chi2
n=16;sq=0.0023;p=0.025
low = ((n-1)*sq)/ chi2.ppf(1-p, n-1)
up = ((n-1)*sq)/ chi2.ppf(p, n-1)
print ('low=',round(low,4))
print ('up=',round(up,4))
output
low= 0.0013
up= 0.0055
norm1_confidence_interval_4var(n=16, var=0.0023, alpha=0.05)
output
[0.0013, 0.0055]
1.4 Python双正态总体均值差区间估计
1.4.1 方差 σ 2 \sigma^2 σ2已知
假设 σ 1 2 , σ 2 2 \sigma_1^2,\sigma_2^2 σ12,σ22都已知,求 μ 1 − μ 2 \mu_1-\mu_2 μ1−μ2的置信度为 1 − α 1 - \alpha 1−α的置信区间
由于
X
ˉ
∼
N
(
μ
1
,
σ
1
2
)
\bar{X} \sim N(\mu_1, \sigma_1^2)
Xˉ∼N(μ1,σ12),
Y
ˉ
∼
N
(
μ
2
,
σ
2
2
)
\bar{Y} \sim N(\mu_2, \sigma_2^2)
Yˉ∼N(μ2,σ22),并且两者独立,得到:
X
ˉ
−
Y
ˉ
∼
N
(
μ
1
−
μ
2
,
σ
1
2
n
1
+
σ
2
2
n
2
)
\bar{X} - \bar{Y} \sim N(\mu_1 - \mu_2, \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2})
Xˉ−Yˉ∼N(μ1−μ2,n1σ12+n2σ22)
因此有:
Z
=
(
X
ˉ
−
Y
ˉ
)
−
(
μ
1
−
μ
2
)
σ
1
2
n
1
+
σ
2
2
n
2
∼
N
(
0
,
1
)
Z=\frac{(\bar{X} - \bar{Y}) - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}}\sim N(0,1)
Z=n1σ12+n2σ22(Xˉ−Yˉ)−(μ1−μ2)∼N(0,1)
由
P
(
−
z
α
/
2
<
Z
<
z
1
−
α
/
2
)
=
1
−
α
P(-z_{\alpha/2} < Z < z_{1-\alpha/2}) = 1 - \alpha
P(−zα/2<Z<z1−α/2)=1−α 即得:
P
(
X
ˉ
−
Y
ˉ
−
z
α
/
2
σ
1
2
n
1
+
σ
2
2
n
2
<
μ
1
−
μ
2
<
X
ˉ
−
Y
ˉ
+
z
α
/
2
σ
1
2
n
1
+
σ
2
2
n
2
)
=
1
−
α
P\left(\bar{X} - \bar{Y} - z_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}< \mu_1 - \mu_2 < \bar{X} - \bar{Y} + z_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}\right) = 1 - \alpha
P
Xˉ−Yˉ−zα/2n1σ12+n2σ22<μ1−μ2<Xˉ−Yˉ+zα/2n1σ12+n2σ22
=1−α
所以两均值差的置信区间为:
(
X
ˉ
−
Y
ˉ
−
z
α
/
2
σ
1
2
n
1
+
σ
2
2
n
2
,
X
ˉ
−
Y
ˉ
+
z
α
/
2
σ
1
2
n
1
+
σ
2
2
n
2
)
\left(\bar{X} - \bar{Y} - z_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}, \bar{X} - \bar{Y} + z_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}\right)
Xˉ−Yˉ−zα/2n1σ12+n2σ22,Xˉ−Yˉ+zα/2n1σ12+n2σ22
同理可求得,两均值差的置信度为 $ 1 - \alpha $ 的置信上限为:
X
ˉ
−
Y
ˉ
+
Z
1
−
α
/
2
σ
1
2
n
1
+
σ
2
2
n
2
\bar{X} - \bar{Y} + Z_{1-\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}
Xˉ−Yˉ+Z1−α/2n1σ12+n2σ22
两均值差的置信度为 $ 1 - \alpha $ 的置信下限为:
X
ˉ
−
Y
ˉ
−
z
1
−
α
/
2
σ
1
2
n
1
+
σ
2
2
n
2
\bar{X} - \bar{Y} - z_{1-\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}
Xˉ−Yˉ−z1−α/2n1σ12+n2σ22
例12-6:为比较两种农产品的产量,选择18块条件相似的试验田,采用相同的耕作方法做实验,结果播种甲品种的8块试验田的单位面积产量和播种乙品种的10块试验田的单
位面积产量分别如表12-2所示。两种农产品的产量如下:
| 名称 | 产量1 | 产量2 | 产量3 | 产量4 | 产量5 | 产量6 | 产量7 | 产量8 | 产量9 | 产量10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 甲品种 | 628 | 583 | 510 | 554 | 612 | 523 | 530 | 615 | - | - |
| 乙品种 | 535 | 433 | 398 | 470 | 567 | 480 | 498 | 560 | 503 | 426 |
假定每个品种的单位面积产量均服从正态分布,甲品种产量的方差为2140,乙品种产量的方差为3250,试求这两个品种平均面积产量差的置信区间(取a=0.05)。
import numpy as np
import scipy.stats as ss
x=[628,583,510,554,612,523,530,615]
y=[535,433,398,470,567,480,498,560,503,426]
n1=len(x)
n2=len(y)
x_bar=np.mean(x)
y_bar=np.mean(y)
sigma1_2=2140
sigma2_2=3250
alpha = 0.05
low = x_bar - y_bar-ss.norm.ppf(q = 1 - alpha/2) * np.sqrt(sigma1_2/n1+sigma2_2/n2)
up = x_bar - y_bar+ss.norm.ppf(q = 1 - alpha/2) * np.sqrt(sigma1_2/n1+sigma2_2/n2)
print ('low=',round(low,4))
print ('up=',round(up,4))
output
low= 34.6669
up= 130.0831
ci = norm2_ci_4difference_mean(x_bar,y_bar,n1,n2,alpha,s1_2=None,s2_2=None,sigma1_2=sigma1_2,sigma2_2=sigma2_2)
print(f"{(1-alpha)*100}%置信区间为:{ci}")
output
95.0%置信区间为:[34.6669, 130.0831]
1.4.2 方差 σ 2 \sigma^2 σ2未知,但相等 σ 1 2 = σ 2 2 \sigma_{1}^2=\sigma_{2}^2 σ12=σ22
1.5 两方差都未知时两均值差的置信区间
设两方差均未知,但 σ 1 2 = σ 2 2 \sigma_1^2 = \sigma_2^2 σ12=σ22。此时由于 Z = ( X ˉ − Y ˉ ) − ( μ 1 − μ 2 ) σ 1 2 n 1 + σ 2 2 n 2 ∼ N ( 0 , 1 ) Z=\frac{(\bar{X} - \bar{Y}) - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}}\sim N(0,1) Z=n1σ12+n2σ22(Xˉ−Yˉ)−(μ1−μ2)∼N(0,1) , ( n 1 − 1 ) S 1 2 σ 2 ∼ χ 2 ( n 1 − 1 ) \frac{(n_1-1)S1^2}{\sigma^2} \sim \chi^2(n_1-1) σ2(n1−1)S12∼χ2(n1−1), ( n 2 − 1 ) S 2 2 σ 2 ∼ χ 2 ( n 2 − 1 ) \frac{(n_2-1)S2^2}{\sigma^2} \sim \chi^2(n_2-1) σ2(n2−1)S22∼χ2(n2−1)
所以 ( n 1 − 1 ) S 1 2 σ 1 2 + ( n 2 − 1 ) S 2 2 σ 2 2 ∼ χ 2 ( n 1 + n 2 − 2 ) \frac{(n_1-1)S_1^2}{\sigma_1^2} + \frac{(n_2-1)S_2^2}{\sigma_2^2} \sim \chi^2(n_1+n_2-2) σ12(n1−1)S12+σ22(n2−1)S22∼χ2(n1+n2−2)。
由此可得:
T = ( X ˉ − Y ˉ − ( μ 1 − μ 2 ) ( 1 n 1 + 1 n 2 ) S 2 ∼ t ( n 1 + n 2 − 1 ) T=\frac{(\bar{X} - \bar{Y} - (\mu_1 - \mu_2)}{\sqrt{(\frac{1}{n_1}+\frac{1}{n_2})S^2}} \sim t(n_1+n_2-1) T=(n11+n21)S2(Xˉ−Yˉ−(μ1−μ2)∼t(n1+n2−1)。
其中, S 2 = ( n 1 − 1 ) S 1 2 + ( n 2 − 1 ) S 2 2 ( n 1 − 1 ) + ( n 2 − 1 ) S^2 = \frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{(n_1-1)+(n_2-1)} S2=(n1−1)+(n2−1)(n1−1)S12+(n2−1)S22, S 1 S_1 S1和 S 2 S_2 S2分别是样本1和样本2的标准差。
同样由 P ( − t 1 − α / 2 ( n 1 + n 2 − 2 ) < T < t 1 − α / 2 ( n 1 + n 2 − 2 ) ) = 1 − α P\left(-t_{1-\alpha/2}(n_1+n_2-2) < T < t_{1-\alpha/2}(n_1+n_2-2)\right) = 1 - \alpha P(−t1−α/2(n1+n2−2)<T<t1−α/2(n1+n2−2))=1−α,
解不等式即得两均值差的置信度为 1 − α 1 - \alpha 1−α 的置信区间为:
( X ˉ − Y ˉ ± t 1 − α / 2 ( n 1 + n 2 − 2 ) ⋅ ( 1 n 1 + 1 n 2 ) S 2 ) \left(\bar{X} - \bar{Y} \pm t_{1-\alpha/2}(n_1+n_2-2) \cdot \sqrt{(\frac{1}{n_1}+\frac{1}{n_2})S^2}\right) (Xˉ−Yˉ±t1−α/2(n1+n2−2)⋅(n11+n21)S2)
同理可求得两均值差的置信度为 1 − α 1 - \alpha 1−α的置信上限为:
( X ˉ − Y ˉ + t 1 − α / 2 ( n 1 + n 2 − 2 ) ⋅ ( 1 n 1 + 1 n 2 ) S 2 ) \left(\bar{X} - \bar{Y} + t_{1-\alpha/2}(n_1+n_2-2) \cdot \sqrt{(\frac{1}{n_1}+\frac{1}{n_2})S^2}\right) (Xˉ−Yˉ+t1−α/2(n1+n2−2)⋅(n11+n21)S2)
两均值差的置信度为 1 − α 1 - \alpha 1−α 的置信下限为:
( X ˉ − Y ˉ − t 1 − α / 2 ( n 1 + n 2 − 2 ) ⋅ ( 1 n 1 + 1 n 2 ) S 2 ) \left(\bar{X} - \bar{Y} - t_{1-\alpha/2}(n_1+n_2-2) \cdot \sqrt{(\frac{1}{n_1}+\frac{1}{n_2})S^2}\right) (Xˉ−Yˉ−t1−α/2(n1+n2−2)⋅(n11+n21)S2)
在上一例题12-6中,如果不知道两种品种产量的方差,但已知两者相同,试求这两个品种平均面积产量差的置信区间(取a=0.05)。
import numpy as np
import scipy.stats as ss
x=[628,583,510,554,612,523,530,615]
y=[535,433,398,470,567,480,498,560,503,426]
n1=len(x)
n2=len(y)
s1_2=np.var(x)
s2_2=np.var(y)
x_bar=np.mean(x)
y_bar=np.mean(y)
alpha = 0.05
sq=((n1-1)*s1_2+(n2-1)*s2_2)/(n1-1+n2-1)
low = xbar - ybar-ss.t.ppf(1-alpha/2,n1+n2-2)*np.sqrt(sq*(1/n1+1/n2))
up = xbar - ybar+ss.t.ppf(1-alpha/2,n1+n2-2)*np.sqrt(sq*(1/n1+1/n2))
print ('low=',round(low,4))
print ('up=',round(up,4))
output
low= 32.4209
up= 132.3291
ci = norm2_ci_4difference_mean(x_bar,y_bar,n1,n2,alpha,s1_2,s2_2,sigma1_2=None,sigma2_2=None)
print(f"{(1-alpha)*100}%置信区间为:{ci}")
output
95.0%置信区间为:[32.4209, 132.3291]
1.6 Python双正态总体方差比区间估计
此时虽然可以就均值是否已知分两种情况讨论方差的区间估计,但在实际中, μ \mu μ已知的情形是极为罕见的,所以只讨论在没有位置的情况下,方差 σ 2 \sigma^2 σ2的置信区间。
由于 ( n 1 − 1 ) S 1 2 σ 2 ∼ χ 2 ( n 1 − 1 ) \frac{(n_1-1)S_1^2}{\sigma^2} \sim \chi^2(n_1-1) σ2(n1−1)S12∼χ2(n1−1), ( n 2 − 1 ) S 2 2 σ 2 ∼ χ 2 ( n 2 − 1 ) \frac{(n_2-1)S_2^2}{\sigma^2} \sim \chi^2(n_2-1) σ2(n2−1)S22∼χ2(n2−1),并且 S 1 2 S_1^2 S12与 S 2 2 S_2^2 S22相互独立,故 F = ( S 1 2 / σ 1 2 ) / ( S 2 2 / σ 2 2 ) ∼ F ( n 1 − 1 , n 2 − 1 ) F=(S_1^2/\sigma_1^2)/(S_2^2/\sigma_2^2) \sim F(n_1-1,n_2-1) F=(S12/σ12)/(S22/σ22)∼F(n1−1,n2−1)
所以对于给定的置信度
1
−
α
1 - \alpha
1−α,由
P
(
F
α
/
2
(
n
1
−
1
,
n
2
−
1
)
<
S
1
2
/
σ
1
2
S
2
2
/
σ
2
2
<
F
1
−
α
/
2
(
n
1
−
1
,
n
2
−
1
)
)
=
1
−
α
P\left(F_{\alpha/2}(n_1 - 1, n_2 - 1) < \frac{S_1^2/\sigma_1^2}{S_2^2/\sigma_2^2} < F_{1 - \alpha/2}(n_1 - 1, n_2 - 1)\right) = 1 - \alpha
P(Fα/2(n1−1,n2−1)<S22/σ22S12/σ12<F1−α/2(n1−1,n2−1))=1−α,
就可以得出两方差比的置信度为 1 − α 1 - \alpha 1−α 的置信区间:
(
S
1
2
S
2
2
1
F
1
−
α
/
2
(
n
1
−
1
,
n
2
−
1
)
,
S
1
2
S
2
2
1
F
α
/
2
(
n
1
−
1
,
n
2
−
1
)
)
\left( \frac{S_1^2}{S_2^2}\frac{1}{ F_{1 - \alpha/2}(n_1 - 1, n_2 - 1)},\frac{S_1^2}{S_2^2}\frac{1}{ F_{\alpha/2}(n_1 - 1, n_2 - 1)}\right)
(S22S12F1−α/2(n1−1,n2−1)1,S22S12Fα/2(n1−1,n2−1)1)
其中
F
p
(
m
,
n
)
F_p(m, n)
Fp(m,n) 为自由度
(
m
,
n
)
(m, n)
(m,n)的 F 分布的下侧 p 分位数。
例12-7: 甲、乙两台机床分别加工某种轴承,轴承的直径分别服从正态分布 N ( μ 1 , σ 1 2 ) N(\mu_{1},\sigma_{1}^2) N(μ1,σ12), N ( μ 2 , σ 2 2 ) N(\mu_{2},\sigma_{2}^2) N(μ2,σ22) ,从各自加工的轴承中分别抽取若干个轴承测其直径,结果如表12-2所示。
| 机床类型 | 样本容量 | 直径(单位:mm) |
|---|---|---|
| x(机床甲) | 8 | 20.5, 19.8, 19.7, 20.4, 20.1, 20.0, 19.0, 19.9 |
| y(机床乙) | 7 | 20.7, 19.8, 19.5, 20.8, 20.4, 19.6, 20.2 |
试求两台机床加工的轴承直径的方差比的0.95的置信区间。
import numpy as np
import scipy.stats as ss
x=[20.5,19.8,19.7,20.4,20.1,20.0,19.0,19.9]
y=[20.7,19.8,19.5,20.8,20.4,19.6,20.2]
s1_2=np.var(x)
s2_2=np.var(y)
n1=8
n2=7
alpha=0.05
low = s1_2/s2_2*1/ss.f.ppf(1-alpha/2, n1-1, n2-1)
up = s1_2/s2_2*1/ss.f.ppf(alpha/2, n1-1, n2-1)
print ('low=',round(low,4))
print ('up=',round(up,4))
output
low= 0.1422
up= 4.1446
ci = norm2_ci_4var(s1_2,s2_2,n1,n2,alpha)
print(f"{(1-alpha)*100}%置信区间为:{ci}")
output
95.0%置信区间为:[0.1422, 4.1446]
2. Ch13–python 假设检验
2.1 Python单个样本t检验
- 原假设:样本均值等于总体均值(H0: μ = μ0)。
- 备择假设:样本均值不等于总体均值(H1: μ ≠ μ0)。
- 统计量:t统计量,用于比较样本均值与总体均值的差异。
- 应用场景:当总体方差未知且样本量较小时,用于检验单个样本的均值是否与已知总体均值有显著差异。
例13-1:某电脑公司销售经理人均月销售500台电脑,现采取新的广告政策,半年后,随机抽取该公司20名销售经理的人均月销售量数据,具体数据如表6-6所示。问广告策略是否能够影响销售经理的人均月销售量?
表13-1人均月销售量 单位:台
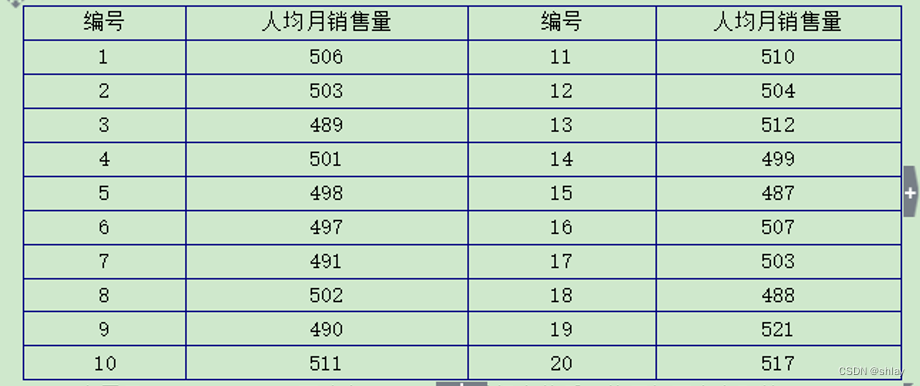
数据文件“ch13_1.xls”下载
import pandas as pd
import numpy as np
#读取数据并创建数据表,名称为data。
data=pd.DataFrame(pd.read_excel('./data/ch13_1.xls '))
#查看数据表前5行的内容
print(data.head())
#取sale数据
x = np.array(data[['sale']])
mu=np.mean(x)
print(mu)
from scipy import stats as ss
print (ss.ttest_1samp(a = x,popmean =500))
output
sale
0 506
1 503
2 489
3 501
4 498
501.8
TtestResult(statistic=array([0.83092969]), pvalue=array([0.41633356]), df=array([19]))
2.2 Python两个独立样本t检验
- 原假设:两个独立样本的均值相等(H0: μ1 = μ2)。
- 备择假设:两个独立样本的均值不等(H1: μ1 ≠ μ2)。
- 统计量:独立样本t统计量,用于比较两个独立样本的均值差异。
- 应用场景:用于比较两个独立样本群体的均值差异,例如,不同治疗方法的效果比较。
例13-2:表13-2给出了a、b两个基金公司各管理40支基金的价格。试用独立样本t检验方法研究两个基金公司所管理的基金价格之间有无明显的差别(设定显著性水平为5%)。
表13-2 a、b两个基金公司各管理基金的价格 单位:元

数据文件“ch13_2.xls”下载
import numpy as np
from scipy.stats import ttest_ind
#读取数据并创建数据表,名称为data。
data=pd.DataFrame(pd.read_excel('./data/ch13_2.xls '))
#查看数据表前5行的内容
print(data.head())
x = np.array(data[['fa']])
y = np.array(data[['fb']])
t,p=ttest_ind(x,y)
print('t=',round(t[0],4))
print('p=',round(p[0],6))
output
fa fb
0 145 101
1 147 98
2 139 87
3 138 106
4 135 105
t= 14.0498
p= 0.0
2.3 Python配对样本t检验
- 原假设:配对样本的均值差为零(H0: μd = 0)。
- 备择假设:配对样本的均值差不为零(H1: μd ≠ 0)。
- 统计量:配对样本t统计量,用于比较配对样本的均值差异。
- 应用场景:用于比较同一组受试者在不同条件下(如前后测试)的均值差异。
例13-3:为了研究一种政策的效果,特抽取了50支股票进行了试验,实施政策前后股票的价格如表12-3所示。试用配对样本t检验方法判断该政策能否引起研究股票价格的明显变化(设定显著性水平为5%)。
表13-3 政策实施前后的股票价格 单位:元
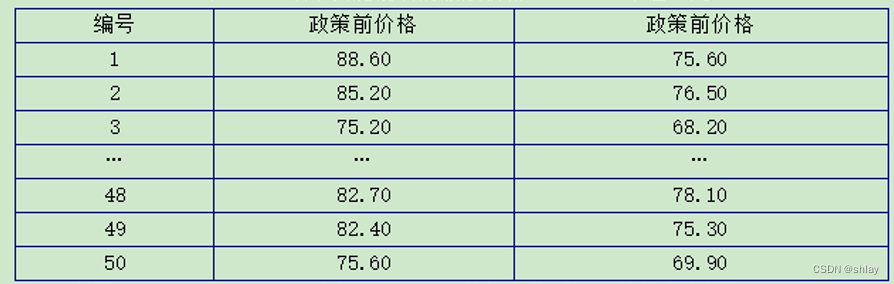
数据文件“ch13_3.xls”下载
import pandas as pd
import numpy as np
from scipy.stats import ttest_rel
#读取数据并创建数据表,名称为data。
data=pd.DataFrame(pd.read_excel('./data/ch13_3.xls '))
#查看数据表前5行的内容
print(data.head())
x = np.array(data[['qian']])
y = np.array(data[['hou']])
t,p=ttest_rel(x,y)
print('t=',round(t[0],4))
print('p=',round(p[0],6))
output
qian hou
0 88.599998 75.599998
1 85.199997 76.500000
2 75.199997 68.199997
3 78.400002 67.199997
4 76.000000 69.900002
t= 12.4305
p= 0.0
2.4 两独立样本 vs 配对样本
两个独立样本t检验(Independent Samples t-test)和配对样本t检验(Paired Samples t-test),也称为相关样本t检验(Related Samples t-test),是两种不同的统计方法,它们用于不同的研究设计和数据类型。以下是它们的主要区别:
2.4.1 两个独立样本t检验
- 研究设计:用于比较两个独立的样本群体(例如,两个不同的实验组或实验组与对照组)。
- 数据类型:每个样本群体的数据是独立的,没有配对关系。
- 目的:检验两个独立样本的均值是否存在显著差异。
- 假设条件:两个样本群体的方差相等(或通过F检验确认方差齐性)。
- 应用场景:适用于两个不同的群体,例如,比较两种不同教学方法的效果。
2.4.2 配对样本t检验
- 研究设计:用于比较同一个样本群体在两个不同条件下的情况(例如,前后测试)。
- 数据类型:数据是成对的,每个样本在两种条件下都有观测值。
- 目的:检验配对样本的均值差是否存在显著差异。
- 假设条件:配对样本的差值应该近似正态分布。
- 应用场景:适用于同一个群体在不同时间点或条件下的比较,例如,比较同一组学生在教学前后的成绩。
2.4.3 总结
- 样本独立性:独立样本t检验的样本是独立的,而配对样本t检验的样本是相关的或配对的。
- 方差假设:独立样本t检验需要假设两个群体的方差相等,而配对样本t检验通常不需要这个假设。
- 数据配对:配对样本t检验利用了数据的配对特性,这可以增加检验的统计功效,因为它控制了某些可能影响结果的变量。
- 研究设计:独立样本t检验适用于两个不同的群体,而配对样本t检验适用于同一个群体在不同条件下的比较。
选择哪种t检验取决于研究设计和数据的特性。如果数据是独立的,应使用独立样本t检验;如果数据是成对的,应使用配对样本t检验。
2.5 Python单样本方差假设检验
- 原假设:样本方差等于已知总体方差(H0: σ² = σ0²)。
- 备择假设:样本方差不等于已知总体方差(H1: σ² ≠ σ0²)。
- 统计量:卡方统计量,用于比较样本方差与总体方差的差异。
- 应用场景:当总体方差已知时,用于检验样本方差是否与总体方差一致。
例13-4:为了研究某基金的收益率波动情况,某课题组对该支基金的连续50天的收益率情况进行了调查研究,调查得到的数据经整理后如表13-4所示。试应用Python 对该数据资料进行假设检验其方差(收益率波动)是否等于1%(设定显著性水平为5%)。
表13-4某基金的收益率波动情况

数据文件“ch13_4.xls”下载
import pandas as pd
import numpy as np
from scipy import stats
#读取数据并创建数据表,名称为data。
data=pd.DataFrame(pd.read_excel('./data/ch13_4.xls '))
#查看数据表前5行的内容
print(data.head())
#取收益率数据
x = np.array(data[['syl']])
n=len(x)
#计算方差
s2=np.var(x)
#计算卡方值
chi2=(n-1)*s2/0.01
print ("卡方值:",chi2)
obs = [102, 102, 96, 105, 95, 100]
exp = [100, 100, 100, 100, 100, 100]
stats.chisquare(obs, f_exp = exp)
output
bh syl
0 1 0.564409
1 2 0.264802
2 3 0.947743
3 4 0.276915
4 5 0.118016
卡方值: 1074.950717665163
2.6 Python双样本方差假设检验
- 原假设:两个独立样本的方差相等(H0: σ1² = σ2²)。
- 备择假设:两个独立样本的方差不等(H1: σ1² ≠ σ2²)。
- 统计量:F统计量,用于比较两个独立样本的方差。
- 应用场景:用于检验两个独立样本群体的方差是否相等,例如,不同处理方法对数据波动的影响。
例13-5:为了研究某两只基金的收益率波动情况是否相同,某课题组对该两支基金的连续20天的收益率情况进行了调查研究,调查得到的数据经整理后如表13-5所示。试使用Python 对该数据资料进行假设检验其方差是否相同(设定显著性水平为5%)。
表13-5某两只基金的收益率波动情况

数据文件“ch13_5.xls”下载
import pandas as pd
import numpy as np
from scipy import stats
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
#读取数据并创建数据表,名称为data。
data=pd.DataFrame(pd.read_excel('./data/ch13_5.xls '))
#查看数据表前5行的内容
print(data.head())
formula = 'returnA~returnB' #~ 隔离因变量和自变量 (左边因变量,右边自变量 )
model = ols(formula,data).fit() # 根据公式数据建模,拟合
results = anova_lm(model) # 计算F和P
print(results)
output
returnA returnB
0 0.424156 0.261075
1 0.898346 0.165021
2 0.521925 0.760604
3 0.841409 0.371380
4 0.211008 0.379541
df sum_sq mean_sq F PR(>F)
returnB 1.0 0.000709 0.000709 0.007744 0.93085
Residual 18.0 1.648029 0.091557 NaN NaN