代码随想录-Day32

news2024/10/6 6:43:46

122. 买卖股票的最佳时机 II

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买，然后在同一天出售。

返回你能获得的最大利润。

示例 1：

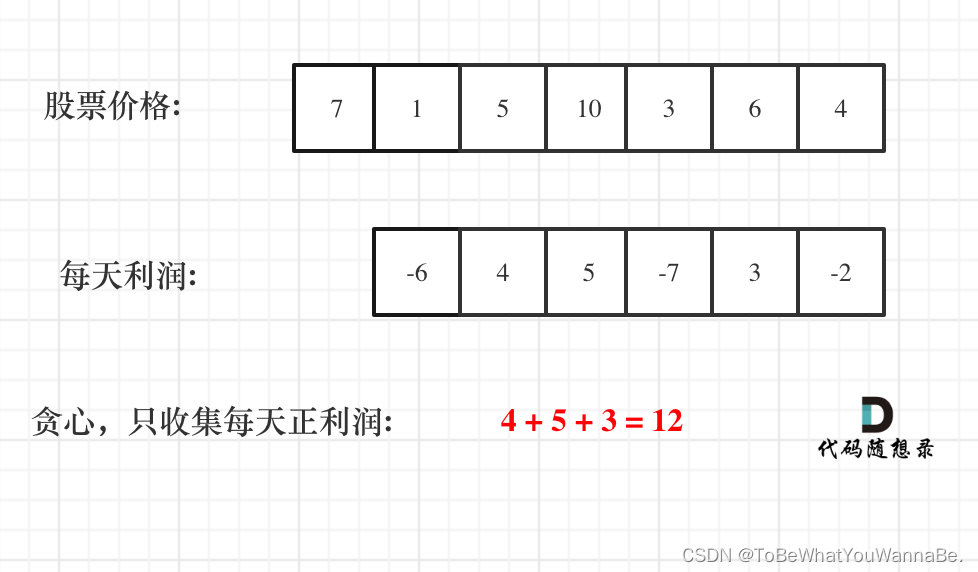
输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。
示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。
示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0 。
在这里插入图片描述

// 贪心思路
class Solution {
    public int maxProfit(int[] prices) {
        int result = 0;
        for (int i = 1; i < prices.length; i++) {
            result += Math.max(prices[i] - prices[i - 1], 0);
        }
        return result;
    }
}

这段代码实现的是计算股票买卖收益的最大利润，这是一个经典的动态规划问题，但这里采用了一种贪心的解法。这个解法是用于解决“在股票价格数组中，只能进行一次买入和一次卖出的情况下，求最大利润”的问题。

解释代码：

函数签名：public int maxProfit(int[] prices) 接受一个整数数组 prices，表示股票每天的价格。
初始化变量 result = 0 用来累计最大利润。
使用一个 for 循环，从数组的第二个元素开始遍历到末尾（i = 1 到 prices.length - 1）。
- 在每次循环中，计算当前天数 i 的价格与前一天 i - 1 的价格之差 prices[i] - prices[i - 1]。
- 使用 Math.max() 函数取这个差值与0的最大值。这样可以确保只有当当天价格高于前一天时（即可以盈利时），才将差值累加到结果中。如果当天价格比前一天低，则不进行交易，结果增加0。
- 每次迭代的结果累加到 result 中。
循环结束后，返回累计的最大利润 result。

总结：

这段代码提供了一个简洁的贪心策略来解决股票交易中的最大利润问题，特别适用于只允许进行一次买入和一次卖出的情况。通过逐天检查能否获得正利润，并立即获取这些利润，从而避免了复杂的动态规划状态维护，降低了算法的时间复杂度至O(n)，其中n为股票价格数组的长度。

55. 跳跃游戏

给你一个非负整数数组 nums ，你最初位于数组的第一个下标。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

示例 1：

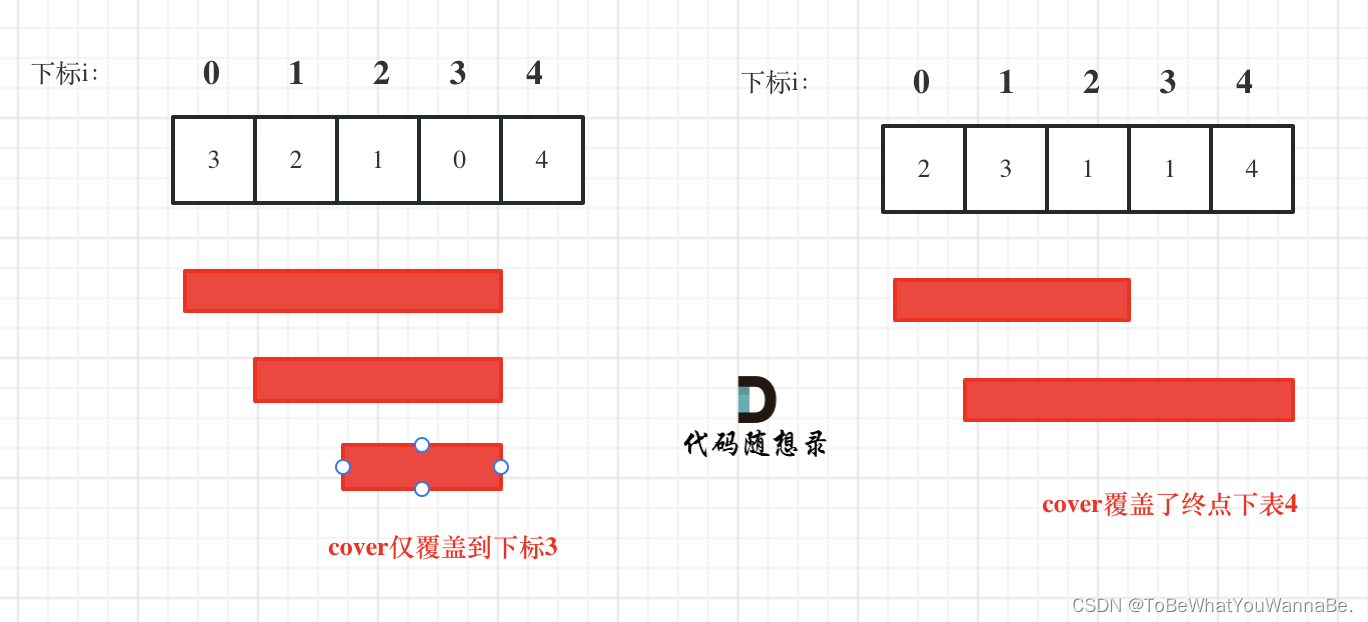
输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ，所以永远不可能到达最后一个下标。
在这里插入图片描述

class Solution {
    public boolean canJump(int[] nums) {
        if (nums.length == 1) {
            return true;
        }
        //覆盖范围, 初始覆盖范围应该是0，因为下面的迭代是从下标0开始的
        int coverRange = 0;
        //在覆盖范围内更新最大的覆盖范围
        for (int i = 0; i <= coverRange; i++) {
            coverRange = Math.max(coverRange, i + nums[i]);
            if (coverRange >= nums.length - 1) {
                return true;
            }
        }
        return false;
    }
}

这段代码是用于解决“跳跃游戏”问题的，该问题是判断在一个给定的非负整数数组 nums 中，初始从数组的第一个位置（下标为0）出发，你是否能够跳到最后一个位置。数组中的每个元素 nums[i] 表示你在该位置上能够跳跃的最大长度。

代码解释：

函数签名：public boolean canJump(int[] nums) 接受一个非负整数数组 nums 作为输入参数。
特殊情况处理：如果数组长度为1，即只有一个位置，自然能跳到最后，所以直接返回 true。
初始化 coverRange = 0，这个变量表示当前能覆盖的最远距离的结束下标。
使用 for 循环，迭代的条件是 i <= coverRange，意味着只要当前位置在已知可达范围内，就继续尝试扩展这个范围。
- 在循环体内，用 Math.max() 更新 coverRange，使其成为当前下标 i 加上从该位置可跳跃的最大距离 nums[i] 的较大值。这样可以确保 coverRange 总是表示当前位置能到达的最远边界。
- 如果在某次迭代中，发现 coverRange 已经大于等于数组最后一个元素的下标（即 coverRange >= nums.length - 1），说明可以跳到最后的位置了，因此提前返回 true。
循环结束后，如果没有提前返回，说明没有找到能跳到数组末尾的路径，返回 false。