0-1背包问题(动态规划)
例题
算法思想:
动态规划的核心思想是将原问题拆分成若干个子问题,并利用已解决的子问题的解来求解更大规模的问题。
主要是状态转移方程和状态

算法描述:
- 初始化一个二维数组dp,大小为(n+1)×(W+1),其中n为物品的个数,W为背包的容量限制。
- 将dp数组的第0行和第0列全部初始化为0,表示背包容量为0或物品个数为0时的最大总价值都为0。
- 对于物品i,从1到n,依次进行以下操作:
- 对于背包容量j,从1到W,依次进行以下操作:
- 如果第i个物品的重量小于等于背包容量j,则可以选择装入该物品或不装入该物品,选择其中总价值较大的方案:
- 如果选择装入该物品,则总价值为dp[i-1][j-w[i]] + v[i],其中w[i]为第i个物品的重量,v[i]为第i个物品的价值;
- 如果选择不装入该物品,则总价值为dp[i-1][j]。
- 取两者中的较大值作为dp[i][j]的值。
- 如果第i个物品的重量大于背包容量j,则无法选择装入该物品,只能选择不装入该物品,即dp[i][j] = dp[i-1][j]。
- 如果第i个物品的重量小于等于背包容量j,则可以选择装入该物品或不装入该物品,选择其中总价值较大的方案:
- 对于背包容量j,从1到W,依次进行以下操作:
- 最终的dp[n][W]即为问题的解,表示在物品个数为n,背包容量为W时的最大总价值。
复杂度分析:
- 时间复杂度:动态规划解法的时间复杂度为O(nW),其中n为物品的个数,W为背包的容量限制。
- 空间复杂度:动态规划解法的空间复杂度为O(nW),需要使用一个二维数组dp来记录子问题的最优解,若是使用滚动数组优化,可以减小空间复杂度,实际上只用开一维数组,O(W)。
正确性分析:
代码:
// 代码一:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
int n, W;
int[] v = new int[110], w = new int[110];
int[][] dp = new int[110][110];
Scanner scanner = new Scanner(System.in);
W = scanner.nextInt();
n = scanner.nextInt();
for(int i = 1; i <= n; i ++ ) {
w[i] = scanner.nextInt();
v[i] = scanner.nextInt();
}
for(int i = 0; i <= W; i ++ ) dp[0][i] = 0;
for(int i = 1; i <= n; i ++ ) {
for(int j = 0; j <= W; j ++ ) {
dp[i][j] = dp[i - 1][j];
if (j >= w[i]) dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - w[i]] + v[i]);
}
}
System.out.println(dp[n][W]);
}
}
// 代码二:(滚动数组优化)
import java.util.Scanner;
// in:
//70 3
//71 100
//69 1
//1 2
public class Main {
public static void main(String[] args) {
int n, W;
int[] v = new int[110], w = new int[110];
int[] dp = new int[1010];
Scanner scanner = new Scanner(System.in);
t = scanner.nextInt();
m = scanner.nextInt();
for(int i = 1; i <= n; i ++ ) {
w[i] = scanner.nextInt();
v[i] = scanner.nextInt();
}
for(int i = 0; i <= W; i ++ ) dp[i] = 0;
for(int i = 1; i <= n; i ++ ) {
for(int j = W; j >= w[i]; j -- ) {
dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);
}
}
System.out.println(dp[W]);
}
}单源最短路径dijkstra(贪心)
算法思想:
Dijkstra算法用于求解单源最短路径问题,即从给定的起点到其他所有节点的最短路径。该算法采用贪心的策略,通过逐步扩展已经确定最短路径的节点集合,来逐步求解所有节点的最短路径。
算法描述:
- 初始化:将起点s到所有其他节点的距离设置为无穷大,将起点s到自身的距离设置为0。
- 创建一个优先队列(最小堆)Q,将起点s加入Q。
- while Q不为空:
- 从Q中选择距离最小的节点u,将u从Q中移除。
- 对于u的所有邻接节点v:
- 计算s到v的距离d,即通过u到v的距离加上s到u的距离。
- 如果d小于v当前的距离,则更新v的距离。
- 如果v不在Q中,则将v加入Q。
- 返回起点s到所有其他节点的最短路径。
复杂度分析:
- 时间复杂度:在每次循环中,需要从Q中选择距离最小的节点,这需要O(V)的时间,其中V是顶点的数量。对于每个节点,需要更新其邻接节点的距离,这需要O(E)的时间,其中E是边的数量。因此,总的时间复杂度为O((V + E) * log V),其中log V是从Q中选择最小值的时间复杂度。
- 空间复杂度:需要使用一个大小为V的优先队列来保存节点,以及一个大小为V的数组来保存每个节点的距离。因此,总的空间复杂度为O(V)。
正确性分析:
- Dijkstra算法通过贪心策略来逐步扩展已经确定最短路径的节点集合,从而求解所有节点的最短路径。该算法的正确性基于贪心选择性质,即每次选择距离最小的节点更新其邻接节点的距离,可以保证得到正确的最短路径。
- 此外,Dijkstra算法还需要满足非负权重的条件,即边的权重不能为负数。如果存在负权重的边,则需要使用其他算法,如Bellman-Ford算法。
代码:
// 朴素版:
int dijkstra()
{
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
for(int i = 1; i <= n; i++)
{
int t = -1;
for(int j = 1; j <= n; j++)
{
if(!visited[j] && (t == -1 || dist[j] < dist[t]))
t = j;
}
visited[t] = true;
for(int j = 1; j <= n; j++)
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
if(dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
// 堆优化版:用邻接表存
int dijkstra(int s)
{
memset(dist, 0x3f, sizeof(dist));
dist[s] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap; // 定义一个小根堆
heap.push({0, s}); // 这里显然要根据距离排序
while(heap.size())
{
PII k = heap.top(); // 取不在集合S中距离最短的点
heap.pop();
int ver = k.second, distance = k.first;
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i]; // i只是个下标,e中在存的是i这个下标对应的点。
if(dist[j] > distance + w[i])
{
dist[j] = distance + w[i];
heap.push({ dist[j], j });
}
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}
矩阵连乘问题(动态规划)

算法思想:
矩阵链乘法问题是关于如何以最佳方式对一系列矩阵进行乘法计算,以最小化标量乘法操作的次数。为了实现这一目的,常用动态规划来解决。
假设我们有一系列矩阵 ( A_1, A_2, ..., A_n ),其中矩阵 ( A_i ) 的维度为 ( p_{i-1} \times p_i )。我们的目标是找到一种括号化方式,使得计算这些矩阵乘积所需的标量乘法次数最少。
动态规划的基本思想是利用子问题的最优解构造全局最优解。我们定义一个二维数组 ( m[i][j] ) 来表示计算矩阵 ( A_i ) 到 ( A_j ) 之间连乘所需的最小标量乘法次数。
一般只需要最后一个矩阵的列数。
s[i][j]记录了在i到j范围内,使得乘法次数最小的分割点k。
通过递归地划分问题并结合子问题的解,我们可以构建出整个问题的最优解。
算法描述:
复杂度分析:
- 时间复杂度: 外层循环有 (n-1) 次迭代(链长度从2到n),第二个循环有 (n) 次迭代,内循环最多有 (n) 次迭代,因此总的时间复杂度为 (O(n^3))。
- 空间复杂度: 我们需要一个 (n \times n) 的二维数组来存储中间结果,因此空间复杂度为 (O(n^2))。
正确性分析:
-
子问题的定义: 我们定义 (m[i][j]) 为计算矩阵 (A_i) 到 (A_j) 连乘所需的最小标量乘法次数。
-
边界条件: 当只有一个矩阵时,乘法次数为零,即 (m[i][i] = 0)。
-
状态转移方程: 对于 (i \le j),我们尝试所有可能的分割点 (k),计算 (m[i][j]) 的最小值,即
m[i][j] = min{ m[i][k] + m[k+1][j] + p[i-1] * p[k] * p[j] }
代码:
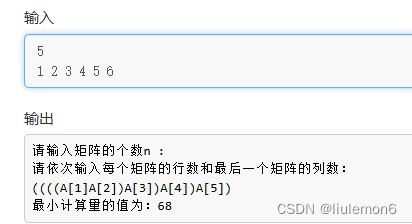
// p[]存放的是所有矩阵的行数和最后一个矩阵的列数
void matrixchain() {
memset(m, 0, sizeof(m));
memset(s, 0, sizeof(s));//初始化数组
for(int r=2; r<=n; r++)//矩阵连乘的规模为r
{
for(int i=1; i <= n-r+1; i ++ ) // 遍历每一种起点
{
j = i+r-1;
// 加的认准三个m[i][j]+m[k][w] + p[i - 1] + p[j] + p[w]
m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j]; // 初始假设将所有矩阵都与第一个矩阵相乘
s[i][j]=i; // s[][]存储各子问题的决策点,即下标
for(int k=i+1; k < j; k++) // 寻找最优值
{
int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(t < m[i][j])
{
m[i][j]=t;
s[i][j]=k;
}
}
}
}
}
// 决策点用来决定打印的加括号的位置
void print(int i,int j) {
if(i == j)
{
cout<<"A["<<i<<"]";
return;
}
cout<<"(";
print(i,s[i][j]);
print(s[i][j]+1,j);//递归1到s[1][j]
cout<<")";
}
最长公共子序列(动态规划)

算法思想:
CS问题可以通过动态规划方法来解决。基本思想是使用一个二维数组存储子问题的解,从而避免重复计算。具体步骤如下:
- 定义状态:设
dp[i][j]表示序列X[1..i]和Y[1..j]的最长公共子序列的长度。 - 状态转移方程:
- 如果
X[i] == Y[j],则dp[i][j] = dp[i-1][j-1] + 1; - 如果
X[i] != Y[j],则dp[i][j] = max(dp[i-1][j], dp[i][j-1])。
- 如果
- 初始条件:当任何一个序列为空时,最长公共子序列的长度为0,即
dp[i][0] = dp[0][j] = 0。

算法描述:
function LCS(X, Y):
m = length(X)
n = length(Y)
# 创建二维数组 dp
dp = array of size (m+1) x (n+1) initialized to 0
# 填充 dp 表
for i from 1 to m:
for j from 1 to n:
if X[i-1] == Y[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
# 返回最终结果
return dp[m][n]
复杂度分析:
时间复杂度
填充一个大小为 (m+1) x (n+1) 的二维数组,每个元素的计算时间为常数时间。因此,总的时间复杂度为 O(m * n),其中 m 和 n 分别是序列 X 和 Y 的长度。
空间复杂度
空间复杂度主要取决于用于存储 dp 数组的空间。二维数组 dp 的大小为 (m+1) x (n+1),所以空间复杂度为 O(m * n)。但是,可以通过空间优化技术(例如使用滚动数组)将空间复杂度降低到 O(min(m, n))。
正确性分析:
基础情况正确性
- 当
i=0或j=0时,dp[i][0]和dp[0][j]都初始化为0,这表示空序列与任何序列的LCS长度为0,这是正确的。
递推关系正确性
- 当
X[i-1] == Y[j-1]时,dp[i][j] = dp[i-1][j-1] + 1,这表示当前字符相等时,最长公共子序列长度增加1。 - 当
X[i-1] != Y[j-1]时,dp[i][j] = max(dp[i-1][j], dp[i][j-1]),这表示要么不包括X[i-1],要么不包括Y[j-1],取两者中较大者作为当前子问题的解。
代码:
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e4 + 10;
string str1, str2;
int c[N][N];
void LCS() {
for(int i = 0; i < str1.size(); i ++ ) {
for(int j = 0; j < str2.size(); j ++ ) {
if(str1[i] == str2[j]) c[i + 1][j + 1] = c[i][j] + 1;
else c[i + 1][j + 1] = max(c[i][j + 1], c[i + 1][j]);
}
}
cout << c[str1.size()][str2.size()] << endl;
}
int main() {
cin >> str1 >> str2;
LCS();
return 0;
}
作业调度问题(回溯法)
每一个作业Ji都有两项任务分别在2台机器上完成。每个作业必须先有机器1处理,然后再由机器2处理。作业Ji需要机器j的处理时间为tji。对于一个确定的作业调度,设Fji是作业i在机器j上完成处理时间。则所有作业在机器2上完成处理时间和f=F2i,称为该作业调度的完成时间和。当作业以相同次序在机器1和机器2上完成处理时,可以得到一种最佳调度,即使该作业调度的完成时间和最小。
算法思想:
对于给定的n个作业,指定最佳作业调度方案,使其完成时间和最小,因此是求一个最优值。
调度必须遵循:
① 一个作业必须先由机器1处理,再由机器2处理,顺序不可颠倒;
② 机器1处理n个作业的顺序必须和机器2处理n个作业的顺序相同(因为只有这样才能使作业调度的完成时间和最小)。
由于是一种作业调度顺序的方案,因此该问题的解空间树是排列树。
算法描述:

复杂度分析:
时间复杂度
- 在最坏情况下,回溯法需要考虑所有可能的解,因此时间复杂度通常为指数级别,即 O(2^n),其中 n 是作业的数量。
- 实际应用中,通过剪枝(约束条件的合理设置)可以显著减少搜索空间,提高效率。
空间复杂度
- 回溯法通常只需要辅助空间来存储当前状态和最优解的临时变量,因此空间复杂度较低,通常为 O(n),其中 n 是作业的数量。
正确性分析:
如何判断某个作业需要在机器2上完成的任务何时开始,这个节点是上一个作业在机器2上完成处理的时间和本作业在机器1上完成处理的时间的较大者
代码:
void Backtrack(int i)
{
if(i>n) //每到达一个叶子结点,一定是产生了一个最优解,因此要更新之前最优解的值
{
if(f<bestf) //更新最优解
{
for(int j=1;j<=n;j++)
bestx[j]=x[j];
bestf=f;
}
}
else
{
for(int j=i;j<=n;j++) //控制展开i-1层结点的各个分支。例如当i=1时,表示在整棵排列树的根结点处,刚要开始探索结点,这时可以展开的分支有1、2、3……
{
f1+=M[x[j]][1]; //计算第i层(个)作业在机器1上的完成处理的时间
if(f2[i-1]>f1) //如果第(i-1)个作业在机器2上的完成处理的时间大于第i个作业在机器1上的完成处理的时间,那么第i个作业想进入机器2,就要等第(i-1)个作业在机器2上完成后再说
f2[i]=f2[i-1]+M[x[j]][2];
else //否则,第i个作业可以在机器1上完成处理后直接进入机器2。
f2[i]=f1+M[x[j]][2];
f+=f2[i]; //计算完第i个作业在机器2上的完成处理的时间,就可以计算出前i个作业在机器2上完成处理的时间和了
if(f<bestf) //截止到这,已经得到一个前i个作业在机器2上完成处理的时间和f,如果f比之前记录的前i个作业在机器2上的完成处理的时间和的最优值bestf都要小,就可以生成第i层结点的孩子结点,继续探索下一层
{
Swap(x[i],x[j]); //把处于同一层的并且使f更小的那个结点拿过来,放到正在探索的这个结点处(这里结合排列数的图可以更好地理解)
Backtrack(i+1); //继续探索以第i层结点为根结点的子树
Swap(x[i],x[j]); //探索完要回溯时,只要做探索前的反“动作”就可以了
}
f-=f2[i]; //探索完要回溯时,只要做探索前的反“动作”就可以了
f1-=M[x[j]][1]; //探索完要回溯时,只要做探索前的反“动作”就可以了
}
}
}会场安排问题(贪心)
算法思想:
只需要关心开始时间和结束时间,,只要集合里面的最大结束时间和当前的开始时间就可以
算法描述:
假设在足够多的会场里安排一批活动,并希望使用尽可能少的会场。设计一个有效的贪心算法进行安排。
贪心策略:采用结束时间最早的会场作为贪心选择。
2. 用数组 s ss 和 f ff 分别存储各活动的开始时间和结束时间。
将数组 s ss 排序,该次序为各活动选择会场的次序。
将数组 f ff 排序。由于会场的结束时间由活动的结束时间决定,排序后的数组也是会场的结束时间点。
3. (1)先为最早开始的活动开辟一个会场,此时会场的最早结束时间为该活动的结束时间。(2)然后遍历剩下的活动。对于每个活动,判断当前最早结束的会场内是否仍有活动:如果有,开辟一个新会场;如果没有,说明当前最早结束的会场能容纳当前的活动,更新会场的结束时间点,保证最早结束的会场最先开始下一个活动。
复杂度分析:
时间复杂度:O(nlogn) 排序
空间复杂度:O(n)
正确性分析:
代码:
#include <iostream>
#include <algorithm>
using namespace std;
//5
//1 23
//12 28
//25 35
//27 80
//36 50
const int N = 1e5 + 10;
int n;
struct hd{
int a, b;
}h[N];
bool cmp(hd h1, hd h2) {
return h1.a < h2.a;
}
int main() {
cin >> n;
for(int i = 0; i < n; i ++ ) cin >> h[i].a >> h[i].b;
sort(h, h + n, cmp);
int res = -1;
for(int i = 0; i < n; i ++ ) {
int j = i + 1, t = 1;
while(h[j].a < h[i].b && j < n) {
t ++;
j ++;
}
res = max(res, t);
}
cout << res << endl;
return 0;
}// 贪心正解:
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cout<<"请输入活动的个数:"<<endl;
cin>>n;
int s[n],f[n];
cout<<"请输入每个活动的开始时间和结束时间:"<<endl;
for(int i=0;i<n;i++)
{
cin>>s[i]>>f[i];
}
sort(s,s+n);//理解一下为什么都要升序
sort(f,f+n);
//会场的最短结束时间次序用j来表示,待分配的活动按i来遍历
int j=0,ans=0;
for(int i=0;i<n;i++)
{
if(s[i] < f[j])
{
ans++;
}
else
{
j++;
}
}
cout<<"最小会场数是:"<<ans<<endl;
return 0;
}
图m着色问题(回溯法)
算法思想:
算法尝试所有可能的染色方案,并使用剪枝操作减少无效搜索,最终输出染色方案的数量。
算法描述:
设图G=(V, E), |V|=n, 颜色数= m, 用邻接矩阵a表示G, 用整数1, 2…m来表示
m种不同的颜色。顶点i所着的颜色用x[i]表示。
问题的解向量可以表示为n元组x={ x[1],…,x[n] }. x[i]∈{1,2,…,m},
解空间树为排序树,是一棵n+1层的完全m叉树.
在解空间树中做深度优先搜索, 约束条件:如果g[j][i]=1 , x[i] ≠ x[j]
复杂度分析:
- 时间复杂度:O(m^n)
- 空间复杂度:O(N^2)
正确性分析:
代码:
一颗排列树,一般时间为O(n!)
#include <iostream>
using namespace std;
const int N = 1e4 + 10;
int m, n, edgenum;
int x[N], g[N][N];
int ans;
int check(int i) {
for(int j = 1; j < i; j ++ ) {
if(g[i][j] && x[i] == x[j]) return false;
}
return true;
}
void dfs(int u) {
if(u > n) {
ans ++;
for(int i = 1; i <= n; i ++ ) {
cout << x[i] << ' ';
}
cout << endl;
return ;
}
else {
for(int i = 0; i < m; i ++ ) {
x[u] = i;
if(check(u))
dfs(u + 1);
x[u] = 0;
}
}
}
int main() {
cin >> n >> m >> edgenum;
for(int i = 0; i < edgenum; i ++ ) {
int a, b;
cin >> a >> b;
g[a][b] = g[b][a] = 1;
}
dfs(1);
if(ans)
cout << "染色方案的数量为:" << ans << endl;
else cout << "无染色方案" << endl;
return 0;
}
// 优化
#include <iostream>
#include <vector>
using namespace std;
const int N = 1e4 + 10;
int m, n, edgenum;
int x[N];
vector<int> g[N];
int ans;
bool check(int i) {
for (int j : g[i]) {
if (x[i] == x[j]) return false;
}
return true;
}
void dfs(int u) {
if (u > n) {
ans++;
for (int i = 1; i <= n; i++) {
cout << x[i] << ' ';
}
cout << endl;
return;
}
for (int i = 0; i < m; i++) {
x[u] = i;
if (check(u)) {
dfs(u + 1);
}
x[u] = -1; // 重置状态
}
}
int main() {
cin >> n >> m >> edgenum;
for (int i = 0; i < edgenum; i++) {
int a, b;
cin >> a >> b;
g[a].push_back(b);
g[b].push_back(a);
}
fill(x, x + N, -1); // 初始化颜色数组为-1
dfs(1);
if (ans)
cout << "染色方案的数量为:" << ans << endl;
else
cout << "无染色方案" << endl;
return 0;
}
旅行售货员问题tsp(回溯法)
算法思想:
它通过递归搜索所有可能的路径,并在每一步进行剪枝(分支限界)来减少不必要的计算,尝试找到最短的环路。其实就是寻找哈密尔顿回路
算法描述:
- 递归终止条件:当
u == citynum时,表示已经访问所有城市,此时需要检查是否可以回到起点并更新最优成本。 - 循环和交换:在每一步中,尝试将当前步的节点与后续节点进行交换以生成不同的路径。
- 剪枝条件:如果当前路径的成本加上从前一个城市到当前城市的成本小于当前已知的最优成本,则继续搜索。
复杂度分析:
- 时间复杂度: ( O(n!) )
- 空间复杂度: ( O(n) )
正确性分析:
代码:
同样是一个排序树
void BackTrack(int u) { // u指的是第u步
if(u == citynum) { // 此时是叶子结点的父节点
if(Graph[x[u - 1]][x[u]] != NoEdge && Graph[x[u]][1] != NoEdge && (Graph[x[u - 1]][x[u]] + Graph[x[u]][1] + currentcost < bestcost || bestcost == max_)) {
bestcost = Graph[x[u - 1]][x[u]] + Graph[x[u]][1] + currentcost;
for(int i = 1; i <= citynum; i ++ ) {
bestx[i] = x[i];
}
}
return;
}
else {
for(int j = u; j <= citynum; j ++ ) {
if(Graph[x[u - 1]][x[j]] != NoEdge && Graph[x[u - 1]][x[j]] + currentcost < bestcost || bestcost == max_) { // 分支和界限
swap(x[u], x[j]);
currentcost += Graph[x[u - 1]][x[u]];
BackTrack(u + 1);
currentcost -= Graph[x[u - 1]][x[u]];
swap(x[u], x[j]);
}
}
}
}N皇后问题(回溯法)
算法思想:
任意两个皇后都不能处于同一行、同一列或同一斜线上。可以把八皇后问题扩展到n皇后问题,即在n×n的棋盘上摆放n个皇后,使任意两个皇后都不能处于同一行、同一列或同一斜线上。

算法描述:
回溯法,解空间树是一个排序树
复杂度分析:
时间复杂度O(n!)
空间复杂度O(n^2)
正确性分析:
代码:dg主对角线,+n防止负值,udg副对角线不会有负值
#include <iostream>
using namespace std;
const int N = 1010;
int n, ans;
int g[N][N];
int col[N], dg[N], udg[N];
void dfs(int u) {
if(u > n) {
ans ++;
for(int i = 1; i <= n ; i++ ) {
for(int j = 1; j <= n; j ++ ) {
if(g[i][j]) {
cout << "q ";
}
else cout << ". ";
}
cout << endl;
}
cout << endl;
return ;
}
else {
for(int i = 1; i <= n; i ++ ) {
if(!col[i] && !dg[i - u + n] && !udg[i + u]) {
col[i] = 1;
dg[i - u + n] = 1;
udg[i + u] = 1;
g[u][i] = 1;
dfs(u + 1);
g[u][i] = 0;
col[i] = 0;
dg[i - u + n] = 0;
udg[i + u] = 0;
}
}
}
}
int main() {
cin >> n;
dfs(1);
cout << ans << endl;
return 0;
}KMP算法(字符串)
算法思想:
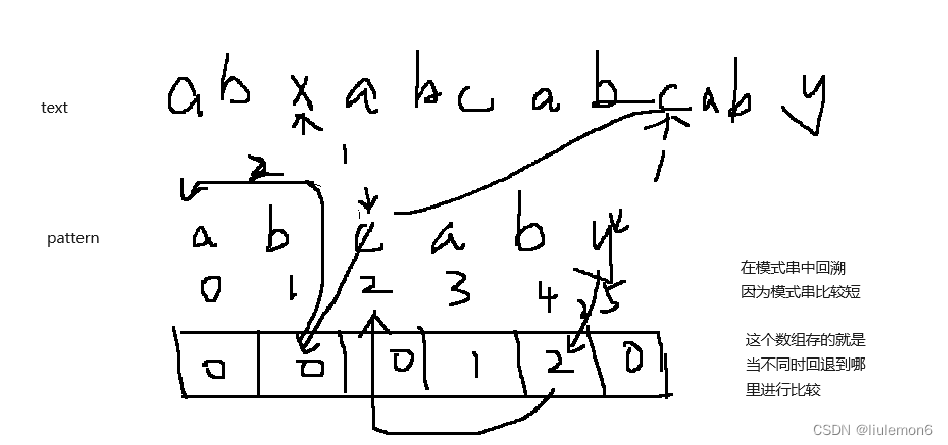
找出模式串在文本串中的出现位置,暴力解法两个循环O(mn)
kmp算法,不用在文本串中回溯了。空间复杂度O(n),时间复杂度O(m+n)
算法描述:
复杂度分析:
正确性分析:
代码:
#include <iostream>
using namespace std;
const int N = 100010, M = 10010; //N为模式串长度,M匹配串长度
int n, m;
int ne[M];
char s[N], p[M]; //s为模式串, p为匹配串
int main()
{
cin >> n >> s+1 >> m >> p+1; //下标从1开始
//求next[]数组
for(int i = 2, j = 0; i <= m; i++)
{
while(j && p[i] != p[j+1]) j = ne[j];
if(p[i] == p[j+1]) j++;
ne[i] = j;
}
//匹配操作
for(int i = 1, j = 0; i <= n; i++)
{
while(j && s[i] != p[j+1]) j = ne[j]; // 回溯
if(s[i] == p[j+1]) j++;
if(j == m) // 满足匹配条件,打印开头下标, 从0开始
{
//匹配完成后的具体操作
//如:输出以0开始的匹配子串的首字母下标
//printf("%d ", i - m); (若从1开始,加1)
j = ne[j]; //再次继续匹配
}
}
return 0;
}







![js 前端 Function.prototype.call.call(0[‘toString‘], *, 16)](https://img-blog.csdnimg.cn/direct/99fef0b4adb44229a921d65a70b4f513.png)