目录

一、问题描述

二、解题思路

1.总体思路（DFS+BFS结合）

2.下面举具体例子来对思路进行解释

(1)返回值在一侧的情况

(2)返回值在两侧的情况

三、代码实现

四、刷题链接

---

一、问题描述

二、解题思路

1.总体思路（DFS+BFS结合）

        使用深度遍历DFS算法获得目标结点所在路径（不包含目标结点和根节点），保存在ArrayList中，同时我们可以根据下标可以知道祖先结点距离目标结点的距离（dis），根据这个差值（k-dis），我们就可以使用广度优先遍历(层序遍历BFS算法)来求祖先节点的第（k-dis）层的子孙结点。

2.下面举具体例子来对思路进行解释

---

(1)返回值在一侧的情况

再来看一个例子target=1，k=2时：

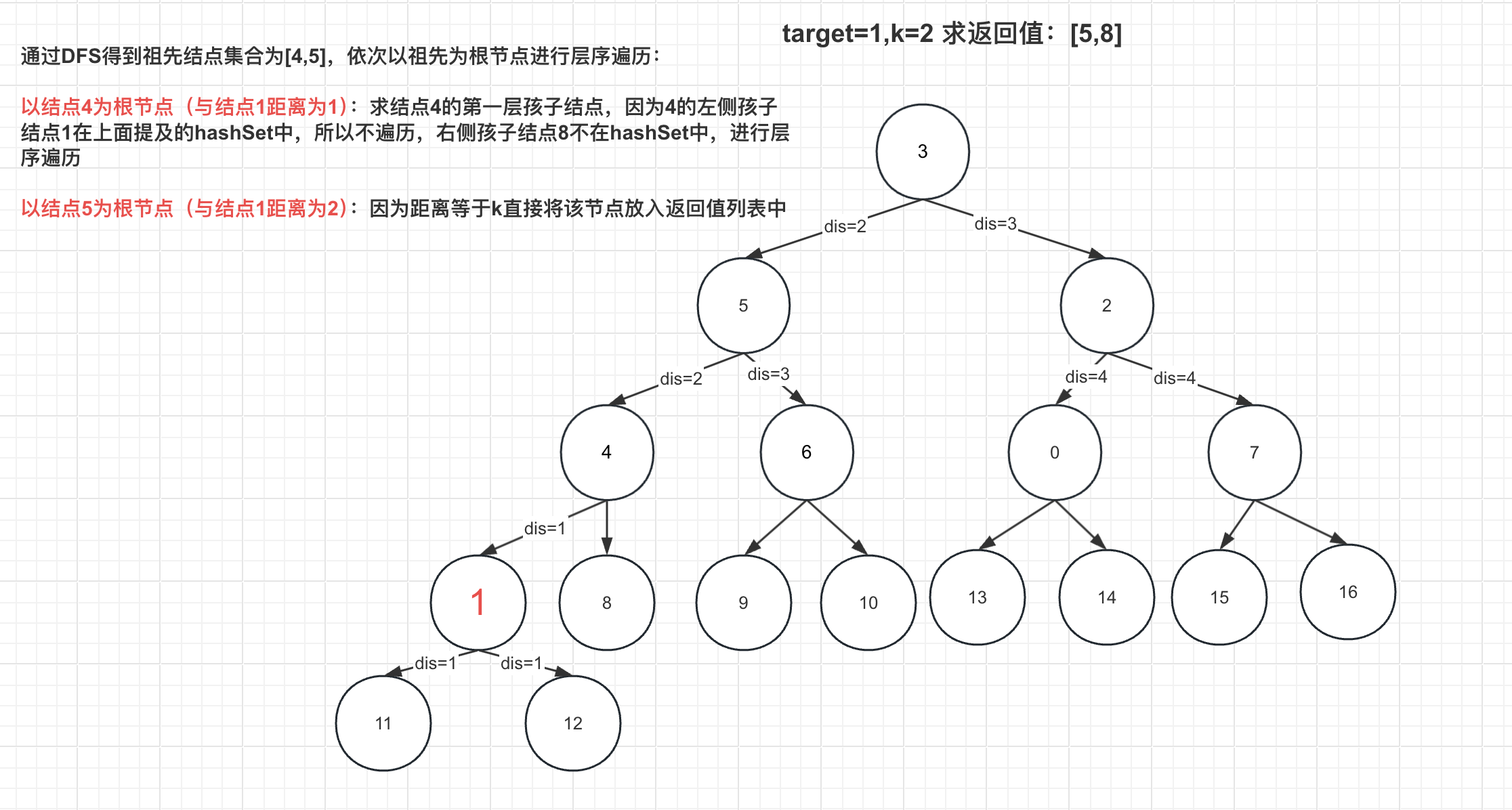
(2)返回值在两侧的情况

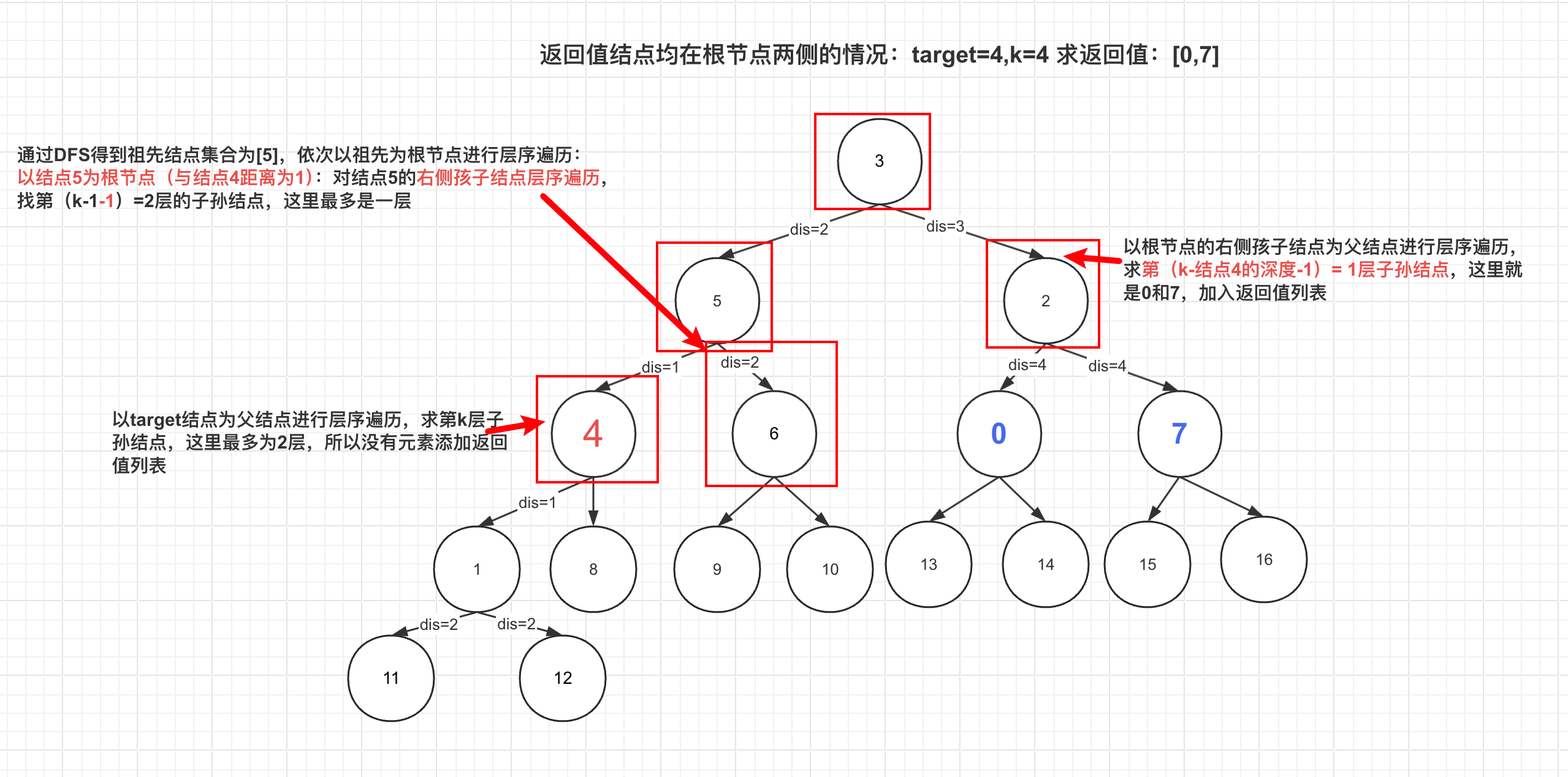
画红色框框的是需要比较的几个关键结点。

三、代码实现

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 *   public TreeNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    int depth=0;
    TreeNode resNode=new TreeNode(-1);
    HashSet<Integer> findSet=new HashSet<>();
    ArrayList<Integer> arr = new ArrayList<>();
    ArrayList<TreeNode> nodes=new ArrayList<>();
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param root TreeNode类 
     * @param target int整型 
     * @param k int整型 
     * @return int整型一维数组
     */
    public ArrayList<Integer> distanceKnodes (TreeNode root, int target, int k) {
        boolean isSide=false;
        boolean isleft=false;
        if(k==0){
            arr.add(target);
            return arr;
        }
        if(root.val==target){//直接执行bfs即可
            bfs(root.left,k-1);
            bfs(root.right,k-1);
            return arr;
        }
        // 先检查是否在左侧
        dfs(root.left,target,1);
        if(depth!=0){
            isleft=true;
        }else{
            dfs(root.right,target,1);
        }
        if(depth<k){
            isSide=false;
        }else{
            isSide=true;
        }

        if(isSide){//结果都在根节点一侧
            //遍历target子孙结点
            bfs(resNode,k);

            //如果是根节点
            if(k==nodes.size()+1){
                arr.add(root.val);
            }
            for(int i=0;i<nodes.size();i++){
                if(k==i+1){//如果祖先结点路径上存在距离为k的节点，也要返回
                    arr.add(nodes.get(i).val);
                }
                //祖先结点的孩子结点存在距离为k的结点返回（注意避开目标结点所在路径）
                if(nodes.get(i).left!=null&&!findSet.contains(nodes.get(i).left.val)){
                    bfs(nodes.get(i).left,k-i-1-1);
                }
                if(nodes.get(i).right!=null&&!findSet.contains(nodes.get(i).right.val)){
                    bfs(nodes.get(i).right,k-i-1-1);
                }
            }
        }else{//结果分散在根节点两侧
            int diff=k-depth;
            if(isleft){
                //遍历右侧深度为diff-1的结点
                bfs(root.right,diff-1);
            }else{
                //遍历右侧深度为diff-1的结点
                bfs(root.left,diff-1);
            }
            //遍历target子孙结点
            bfs(resNode,k);

            //遍历祖先节点
            for(int i=0;i<nodes.size();i++){
                if(nodes.get(i).left!=null&&!findSet.contains(nodes.get(i).left.val)){
                    bfs(nodes.get(i).left,k-i-1-1);
                }
                if(nodes.get(i).right!=null&&!findSet.contains(nodes.get(i).right.val)){
                    bfs(nodes.get(i).right,k-i-1-1);
                }
                
            }
        }
        
        return arr; 
    }
    //遍历第depth层的结点
    public void bfs(TreeNode root,int depth){
        if(root==null){
            return;
        }
        int layernum=0;//深度是从0开始的
        Queue<TreeNode> nowqueue=new LinkedList<>();
        nowqueue.offer(root);
        int nowlayerNodenum=1;//当前层的剩余结点数量
        int nextlayerNodenum=0;//下一层的结点数量
        while(!nowqueue.isEmpty()){
            TreeNode nownode=nowqueue.poll();
            if(layernum==depth){
                arr.add(nownode.val);
            }
            nowlayerNodenum--;
            
            if(nownode.left!=null){
                nowqueue.offer(nownode.left);
                nextlayerNodenum++;
            }
            if(nownode.right!=null){
                nowqueue.offer(nownode.right);
                nextlayerNodenum++;
            }

            if(nowlayerNodenum==0){
                nowlayerNodenum=nextlayerNodenum;
                layernum++;//开启下一层的遍历操作
                nextlayerNodenum=0;
                if(layernum>depth){
                    break;
                }
            }
        }
    }
    public boolean dfs(TreeNode root,int target,int nowdepth){
        if(root==null){
            return false;
        }
        if(root.val==target){
            depth=nowdepth;
            resNode=root;
            findSet.add(root.val);
            return true;
        }else{
            boolean leftbool=dfs(root.left,target,nowdepth+1);
            boolean rightbool=dfs(root.right,target,nowdepth+1);
            if(leftbool||rightbool){
                nodes.add(root);
                findSet.add(root.val);
                return true;
            }else{
                return false;
            }
        }
    }
}

四、刷题链接

距离是K的二叉树节点_牛客题霸_牛客网