1.题目描述

2.思路

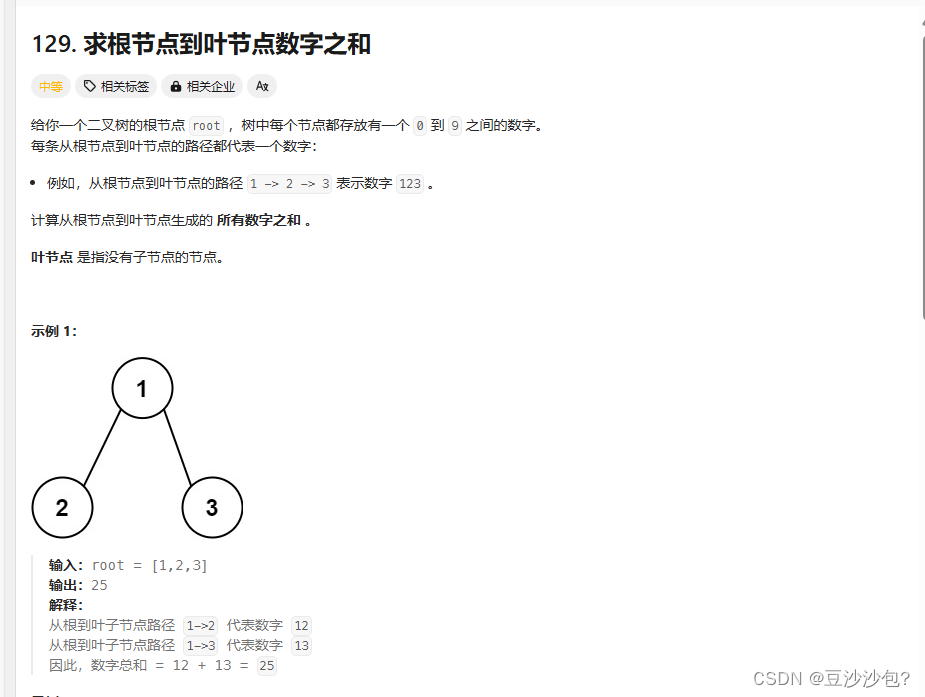
（1）比如

    1
   / \
  2  3

从根节点开始：

初始时，currentSum 为 0。
根节点的值为 1。
更新后的 currentSum = 0 * 10 + 1 = 1。
处理左子节点：

当前 currentSum 为 1（即路径 “1”）。
左子节点的值为 2。
更新后的 currentSum = 1 * 10 + 2 = 12。
处理右子节点：

回到根节点，当前 currentSum 仍为 1。
右子节点的值为 3。
更新后的 currentSum = 1 * 10 + 3 = 13。
（2）
从根节点 root 开始，以 0 作为初始路径值，调用 dfs 方法来计算路径和。
(3)总结一下
递归使用dfs(root,0) 先将root根节点的值设为0
左子树
1）遍历根节点1
刚开始是010+1=1
2）遍历左子树叶子节点2
是110+2=12

右子树
1）遍历根节点1
010+1=1
2）遍历右子树叶子节点3
110+3=13

3.代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int sumNumbers(TreeNode root) {
        return dfs(root,0);
        //辅助函数，深度优先搜索
    }
    private int dfs(TreeNode node,int currsum)
    {
        if(node==null)
        {
            return 0;
        }
        currsum=currsum*10+node.val;

        //如果是叶节点，返回当前值
        if(node.left==null&&node.right==null)
        {
            return currsum;
        }
        //递归计算左右子树的路径之和
        return dfs(node.left,currsum)+dfs(node.right,currsum);
    }

    
}