秋招突击——6/14——复习{（树形DP）树的最长路径，（单调队列优化DP）——最大子序和}—

文章目录

- 引言
- 复习
- - 树形DP——树的最长路径
  - - 实现代码
    - 答疑
  - 单调队列优化DP——最大子序和
  - - 个人实现思路
    - 参考思路分析
    - 实现代码
  - 无重复最长字串
  - - 思路分析
    - 实现代码
- 新作
- - 四数之和
  - - 实现思路
    - - 需要注意的问题
    - 参考代码
    - - 分析思路
      - 实现代码
- 总结

引言

今天好好看看树的最长的路径，自己重新写一下，之前看过了，这个思路并不难的，然后在学一下单调队列优化DP，这个得看准时间，不能一次学过了，能学多少学多少。

复习

树形DP——树的最长路径

以往的学习链接
第一次分析
第二次分析
第三次分析
这道题总得来事主要分为两个部分，分别是
- 使用一维数组表示邻接链表，然后的进行逐个遍历
- 在遍历邻接链表的过程中，分别使用动态规划，计算最大值和次大值
已经分析过很多次了，这里直接给出实现过程

实现代码

#include <iostream>
#include <cstring>
using namespace std;

const int N = 10010;
int h[N],e[2*N],ne[2*N],w[2*N],idx;
int f1[N],f2[N],res = 0;
void add(int a,int b,int c){
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx ++;
}

void dfs(int r,int father){
    // 这里需要对参数进行说明
    // r表示以当前节点为跟节点的子树
    // father表示节点r的父节点

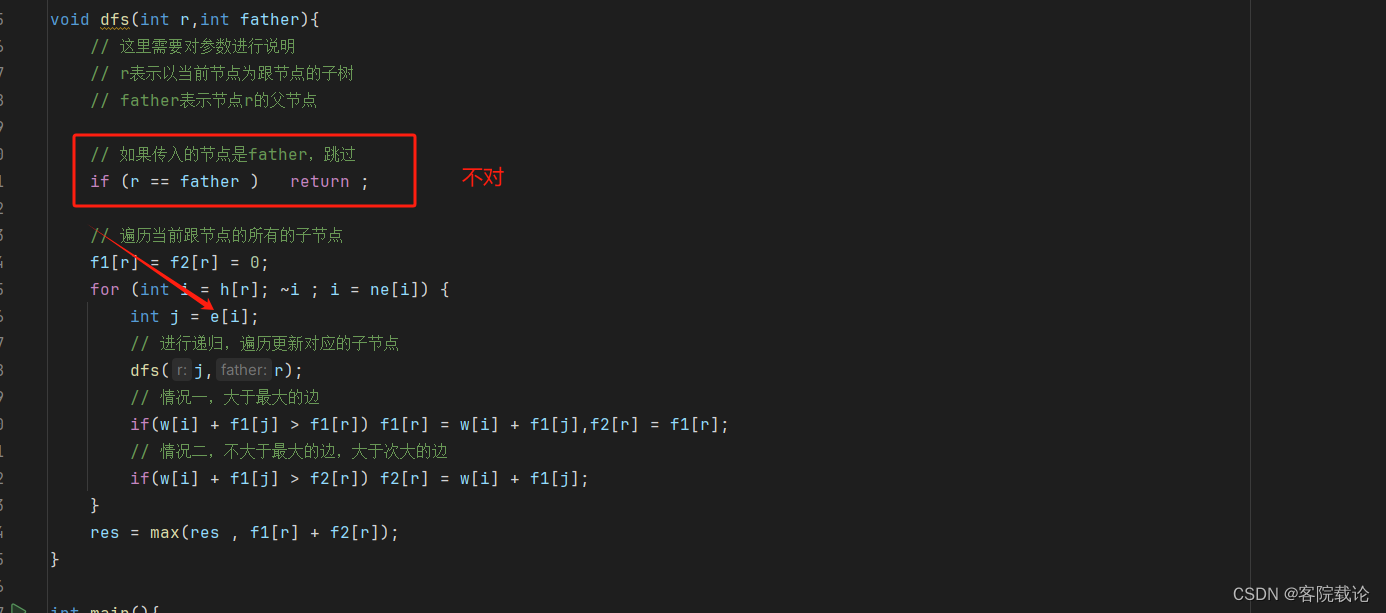
    // 如果传入的节点是father，跳过
    if (r == father )   return ;

    // 遍历当前跟节点的所有的子节点
    f1[r] = f2[r] = 0;
    for (int i = h[r]; ~i ; i = ne[i]) {
        int j = e[i];
        // 进行递归，遍历更新对应的子节点
        dfs(j,r);
        // 情况一，大于最大的边
        if(w[i] + f1[j] > f1[r]) f1[r] = w[i] + f1[j],f2[r] = f1[r];
        // 情况二，不大于最大的边，大于次大的边
        if(w[i] + f1[j] > f2[r]) f2[r] = w[i] + f1[j];
    }
    res = max(res , f1[r] + f2[r]);
}

int main(){
    int n;
    cin>>n;
    memset(h,-1,sizeof(h));
    for (int i = 0; i < n - 1; ++i) {
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c),add(b,a,c);
    }
    // 这里是有一个问题，本质上是一个无向树，是否需要遍历每一个根节点作为子节点
    // 个人猜测是需要，因为认为规定了父子节点的逆序关系
    // 但是这里的代码有没有保存，根本没有办法进行遍历
    dfs(1,-1);
    cout<<res;
    return 0;
}

答疑

这里有两个地方搞不清楚

是否需要遍历所有的定点都当做树的根节点

不需要，因为每一次计算的时候，都是计算了最长边和最短边，最终的路径是最长边和最短边同时相加，所以是一个双向的路径，所以不需要。
任选一个节点作为根节点，然后指定父节点，这个树的唯一拓扑结构就确定了，不会存在出现歧义的情况。
所以不需要遍历每一个节点作为根节点

判定是否为父节点的情况

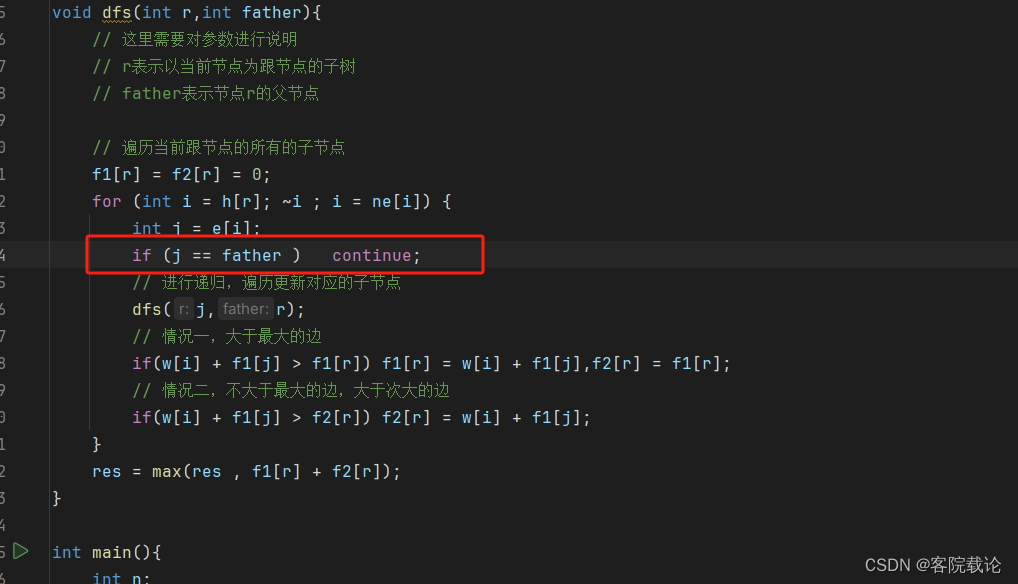
因为是无向边，所以在遍历所有邻接链表的过程中，会遍历到父节点，所以这里需要跳过，所以实在遍历子节点过程中，判定是否为父节点，我原来的代码写错了。

在这里插入图片描述

单调队列优化DP——最大子序和

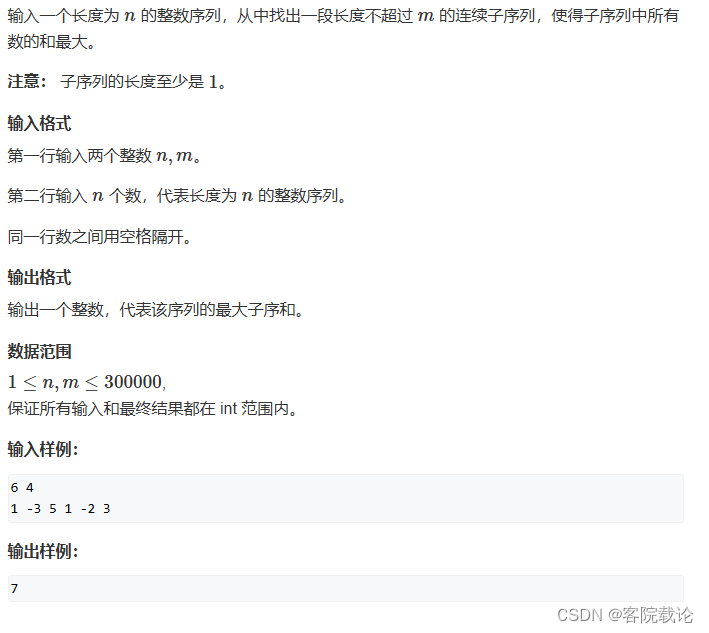
题目内容如下，这是一个单调队列优化DP，先给我五分钟，看一下，写一下思路。

个人实现思路

找一个连续子序列，使其和最大。一个子序列明显是包含了左端点和右端点，这里的直接暴力搜索，因该可以的。最终的时间复杂度是n的平方，但是这里有30万个节点，最终的结果肯定超过了运行的时间，不行。
如何优化暴力搜索？
- 会不会存在子串的情况，因为每一次都是完全从左到右的扫描的话，会存在重复使用子区间的情况，所以还是得想想看怎么弄，怎么优化？
- 是不是状态DP，不是的，这是一个连续的数字，如果不是连续的数字，就可能是状态DP
- 状态压缩DP，也不像，这里仅仅是有两个状态

真的服了，我这是完全没有看题，看成了任意长度，绝了，这是长度不超过m的连续子序列问题
看清题目！！！！！！！！！！

参考思路分析

这里暂时理清了一部分思路，但是还是没有完全看懂，这个单调队列怎么推出来的，怎么写出来的。
首先说一下问题转换
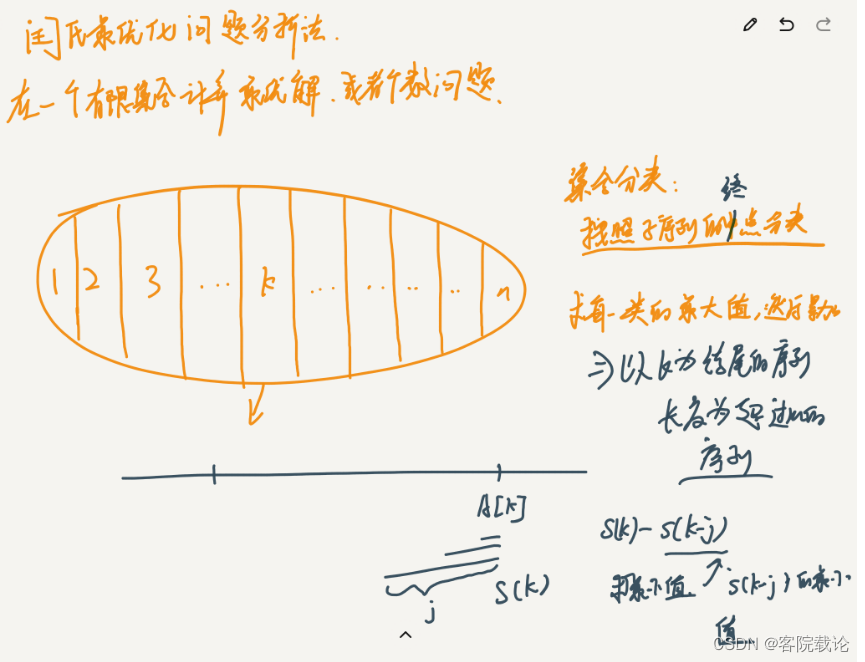
- 将一个序列的最优值变成了的不同终点的序列中，计算最大值，再转成计算Sj的最小值
这里是有问题的，这里是计算{K-m，K-j}的最小值，是这个区间的最小值，怎么就变成了求他的最小值，编程了再{K-m，K}的序列中，计算以K-m为起点的，长度小于等于m的最小的连续序列====》计算最小值？怎么转换的？
正常不应该是找出从{i-m}到j的不同的序列，找出其中的最小值吗？
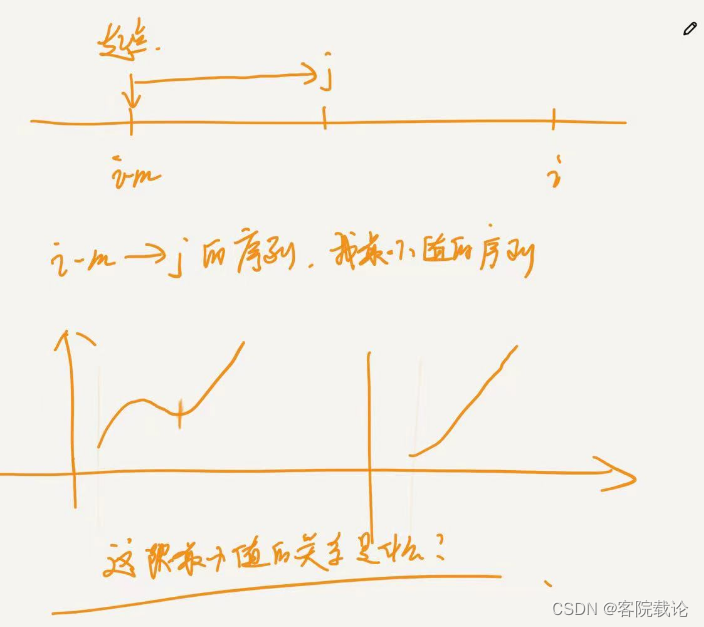
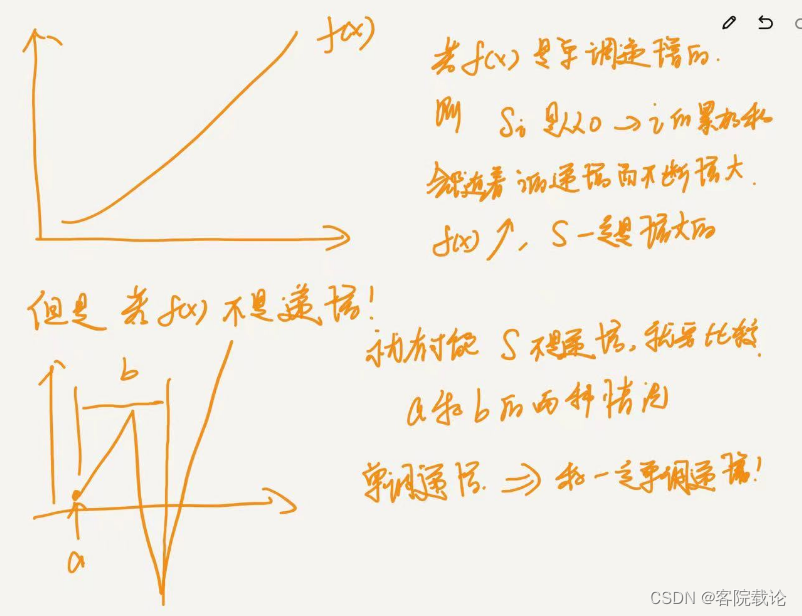
上述前提有一个朴素的证明，那就是如果你下一个要增加的数字是不断递增的，那么你的结果就一定是越大的，但是如果你下一个数字不是单调递增的，那么你累加和得结果就有可能不是最大的，会变小，所以要比较。

在这里插入图片描述

实现代码

这里直接贴代码，没看懂他的思路
得，还是没有看懂，直接自己debug吧，自己理解吧。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 3e5 + 10;

int n, m;
LL s[N], que[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%lld", &s[i]), s[i] += s[i - 1];

    LL res = -1e18;
    int hh = 0, tt = 0; que[0] = 0;
    for (int i = 1; i <= n; i ++ )
    {
        while (hh <= tt && i - que[hh] > m) hh ++ ;
        res = max(res, s[i] - s[que[hh]]);
        while (hh <= tt && s[que[tt]] >= s[i]) tt -- ;
        que[ ++ tt] = i;
    }
    printf("%lld\n", res);
    return 0;
}

作者：一只野生彩色铅笔
链接：https://www.acwing.com/solution/content/67527/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

无重复最长字串

这道题是中等题，我记得我在华为面试手撕代码的时候做了，但是没有做出来，只通过了部分样例，那个时候是第三次做，没做好。
关键是这道题第一次做，我做过了，第二遍是跟着解析做的，第三次没做出来，但是后续又刷了一遍，这是第四遍，看看哈。
前几次的链接
- 华为面试的结果
- 第二次做
好吧，看错了，原来拿到没做出来的题目是三数之和，这道题也是第二次做，看看哈。二十分钟，做出来。

思路分析

这道题是双指针，使用hashmap维系左右指针所包含的所有的字符串的出现次数，具体实现代码如下

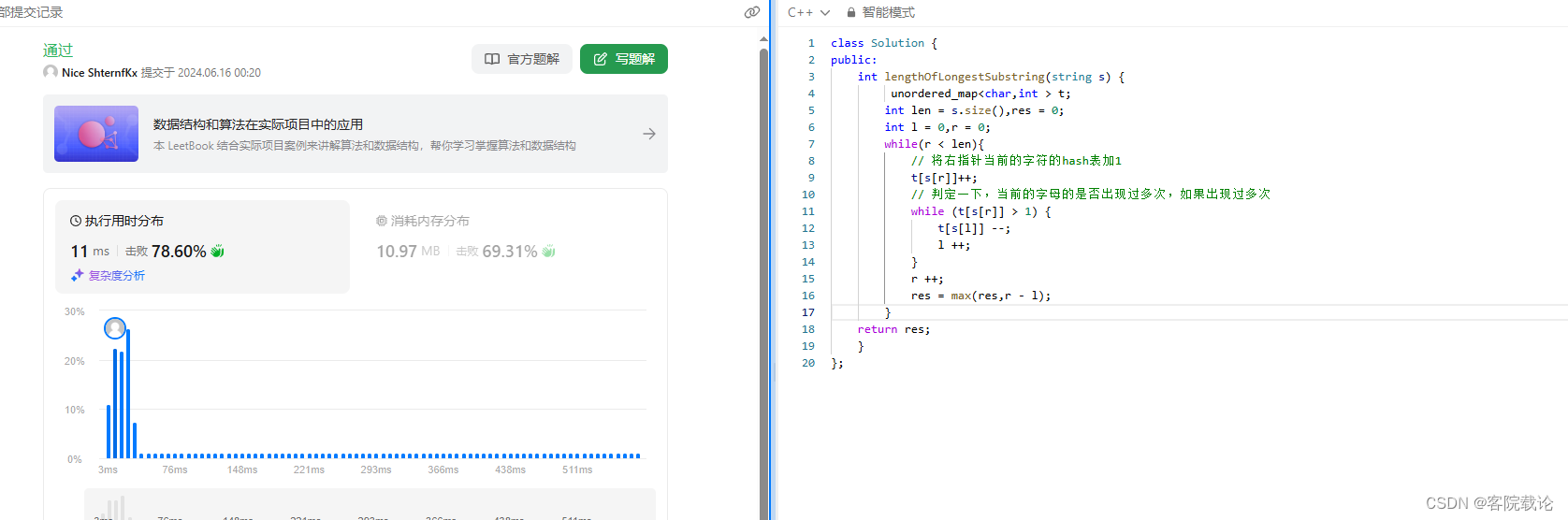
实现代码

#include <iostream>
#include <unordered_map>
using namespace std;

int lengthOfLongestSubstring(string s){
    unordered_map<char,int > t;
    int len = s.size(),res = 0;
    int l = 0,r = 0;
    while(r < len){
        // 将右指针当前的字符的hash表加1
        t[s[r]]++;
        // 判定一下，当前的字母的是否出现过多次，如果出现过多次
        while (t[s[r]] > 1) {
            t[s[l]] --;
            l ++;
        }
        r ++;
        res = max(res,r - l);
    }
    return res;
}
int main(){

}

新作

四数之和

实现思路

n个整数组成的数组：是否是有序的，是否是重复的
要求
- 不重复的四元组
- 累加和为target
这个可以联想到三数之和问题，三数之和问题是拆解成两数之和解决的。
需要将二维数组进行排序。
如果将之转成三数之和，再转成两数之和，时间复杂度就是n的三次方，百万级别，应该能够接受，实现一下
写是写完了，但是又遇到了重复的问题，除了使用set，并不知道如何进行去重了，我得趁着有时间，做一下尝试。
在不使用set的情况下，只能写成这样了，不过肯定还有问题的，这里还是使用set实现一下。

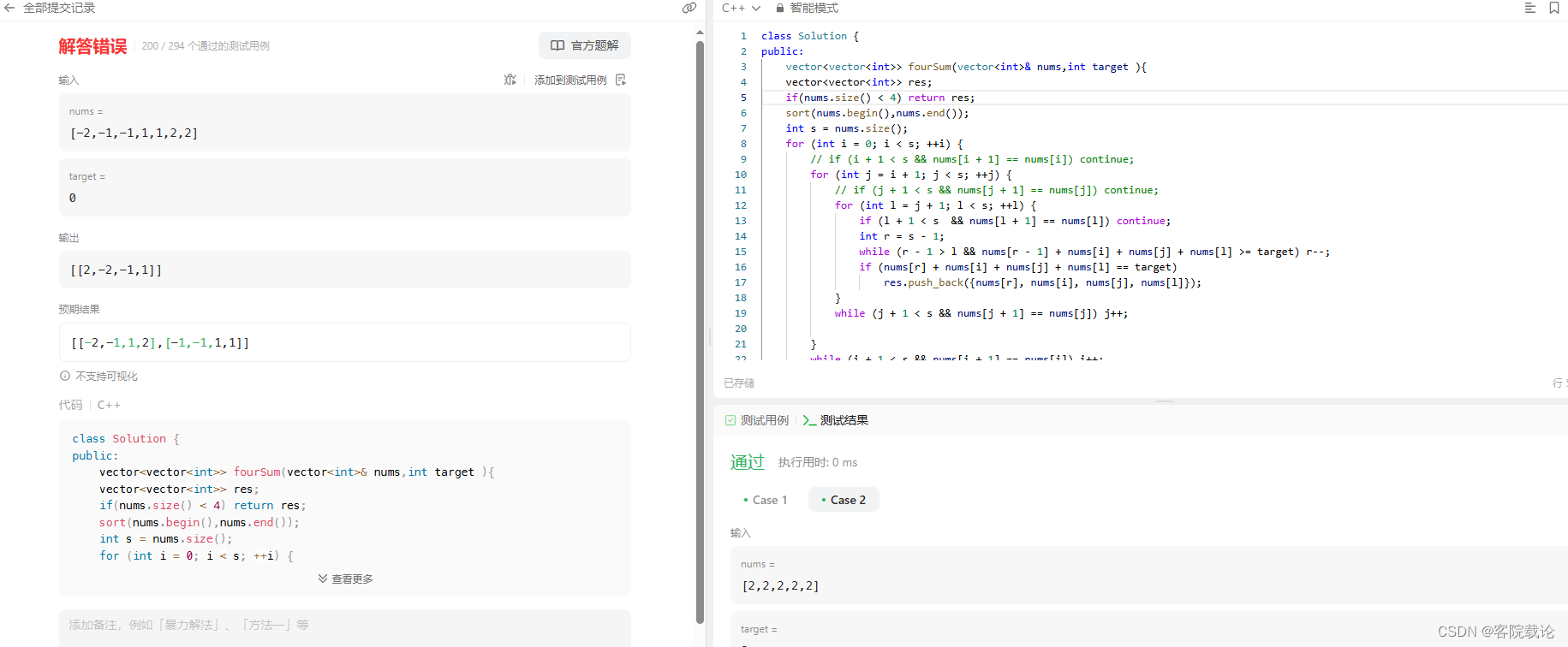
在这里插入图片描述

使用set实现了，效果如下

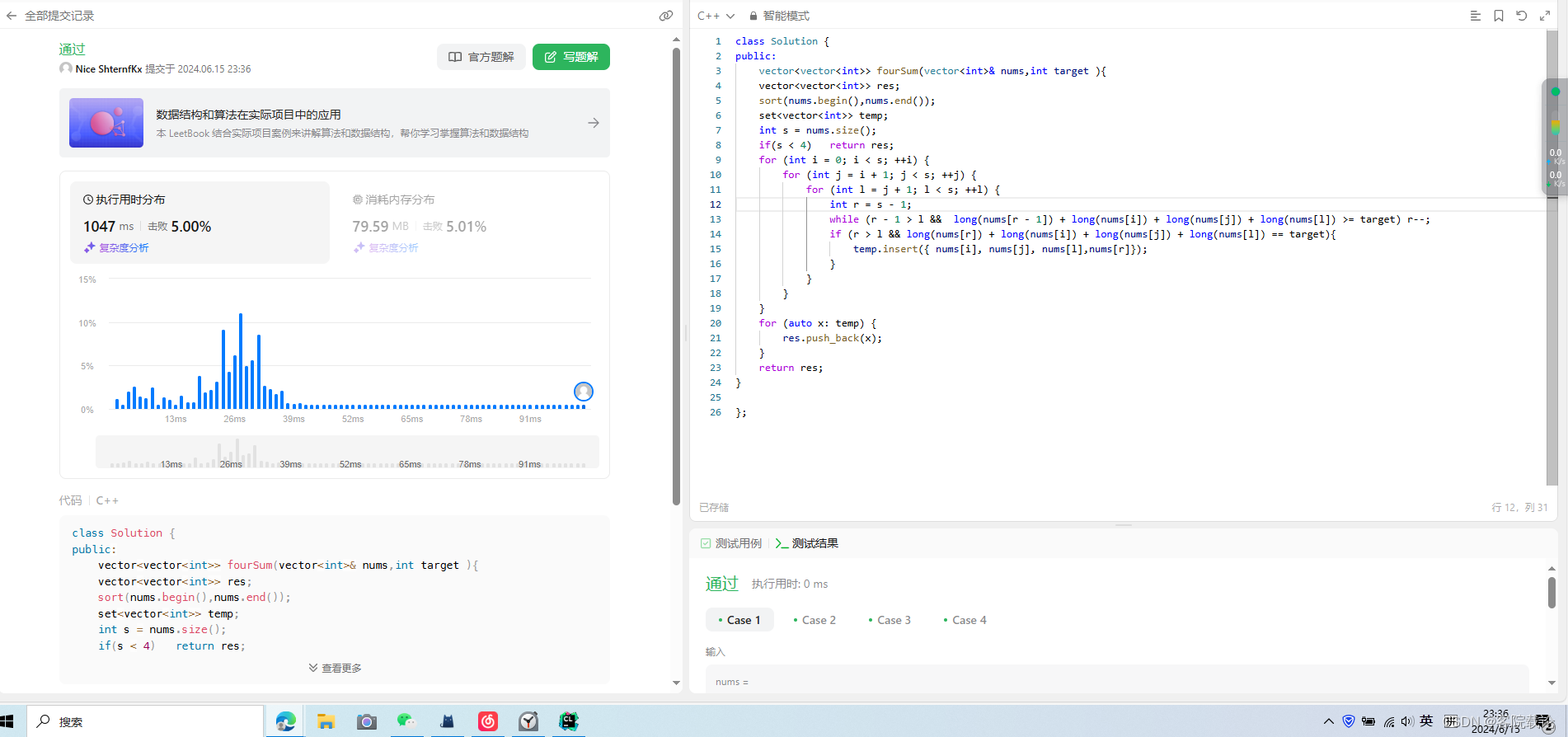
实现代码如下

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums,int target ){
    vector<vector<int>> res;
    sort(nums.begin(),nums.end());
    set<vector<int>> temp;
    int s = nums.size();
    if(s < 4)   return res;
    for (int i = 0; i < s; ++i) {
        for (int j = i + 1; j < s; ++j) {
            for (int l = j + 1; l < s; ++l) {
                int r = s - 1;
                while (r - 1 > l &&  long(nums[r - 1]) + long(nums[i]) + long(nums[j]) + long(nums[l]) >= target) r--;
                if (r > l && long(nums[r]) + long(nums[i]) + long(nums[j]) + long(nums[l]) == target){
                    temp.insert({ nums[i], nums[j], nums[l],nums[r]});
                }
            }
        }
    }
    for (auto x: temp) {
        res.push_back(x);
    }
    return res;
}

};

需要注意的问题

如何更加有效的去重并不知道
如何处理大数相加越界的问题，目前没有好办法。

参考代码

分析思路

基本思路和我的相同
如何去重
这里是和前一个指针进行比较，如果和前一个状态一样，说明后续遍历的结果也是相同的
这里很有细节，如果是第一个定位的元素，就要注明是大于0
后续所有元素，都要确保第一个元素已经访问过了，然后在进行遍历访问。

在这里插入图片描述

和之前的元素进行比较！！！！

处理越界问题

这里直接使用特定情况进行处理，就几个样例。

实现代码

#include <iostream>
#include <vector>
#include <algorithm>
#include <set>
using namespace std;

vector<vector<int>> fourSum(vector<int>& nums,int target ){
    vector<vector<int>> res;
    sort(nums.begin(),nums.end());
    int s = nums.size();
    for (int i = 0; i < s; ++i) {
        if (i && nums[i - 1] == nums[i]) continue;
        for (int j = i + 1; j < s; ++j) {
            // 确保第一个元素已经访问过，然后在和前一个状态进行比较
            if (j > i + 1 && nums[j - 1] == nums[j]) continue;
            for (int l = j + 1; l < s; ++l) {
                if(l > j + 1 && nums[j] == nums[j - 1]) continue;
                int r = s - 1;
                while (r - 1 > l && nums[r - 1] + nums[i] + nums[j] + nums[l] >= target) r--;
                if (nums[r] + nums[i] + nums[j] + nums[l] == target){
                    res.push_back({nums[r], nums[i], nums[j], nums[l]});
                }
            }
        }
    }
    return res;
}

int main(){

}