小数二分

整数二分 是找边界点，而小数二分找的是 近似值。

整数二分是在一个整型数组当中 查找，而小数二分是在数轴中 查找，都是每次可以排除一半的区间，只不过小数二分中while循环内的结束条件和整数二分不一样。

小数二分比较简单，我们直接上题目。

---

题目

给定一个浮点数 $n$，求它的三次方根。

输入格式

共一行，包含一个浮点数 $n$。

输出格式

共一行，包含一个浮点数，表示问题的解。

注意，结果保留 $6$ 位小数。

数据范围

$-10000\le n\le 10000$

输入样例：

1000.00

输出样例：

10.000000

输入环节：

在整数二分中，while 循环里面的 判断是 l < r，也就是 当 l 和 r 相等时会退出循环，但是在数轴上，一直取mid，是不可能相遇的，只能两个下标越来越近，所以我们可以规定他们 “多近” 的时候 再结束循环。

首先先定义左右两个端点，这里我们直接取 整个n 的左右边界（题目里的取值范围）。

然后我们可以在while 循环里面这么写

这里的意思就是 两个点只有 小于等于 这个 1e-8 才会停止循环，也就是说这个 1e-8其实就是我们的精度。

在确定精度的时候有一个小技巧，题目让你 最终打印几位小数，那么你就在此数字上加个2。

比如这个题目中让你 打印 六位小数，所以就写的是 1e-8 。

接着就简单了，还是找 mid。

然后判断 mid 的值，根据 mid 的值在去调整 左右端点。

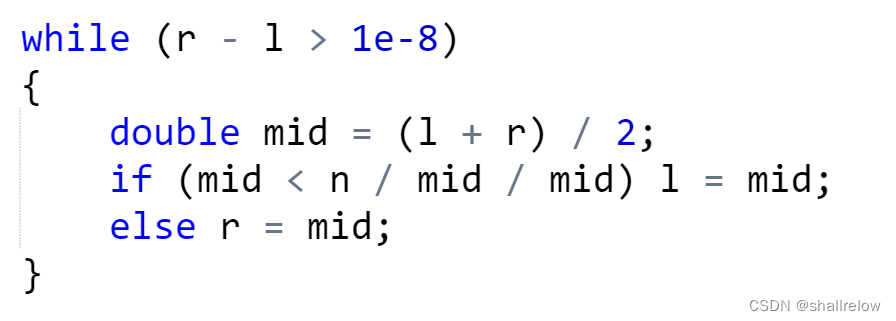
这里 不是写成 mid * mid * mid < n的原因是 如果mid 太大，那么三次方 就有可能 超出存储范围，当然这个题数据比较小， 写成三次方也是可以的，但是 写成这样更保险点。

最后打印我们的l 或 r ，都是可以的。

完整代码如下：

#include <iostream>
using namespace std;

double n;
int main()
{
    scanf("%lf", &n);
    double l = -1e4, r = 1e4;
    
    while (r - l > 1e-8)
    {
        double mid = (l + r) / 2;
        if (mid < n / mid / mid) l = mid;
        else r = mid;
    }
    
    printf("%.6lf", r);
}

---

完