二分查找
感谢灵神的题单
题单:分享丨【题单】二分算法(二分答案/最小化最大值/最大化最小值/第K小) - 力扣(LeetCode)
每天四道题,大概用时一个月刷完,如果没有时间的同学可以学习我总结的算法原理,适用题型,和经典的题单。
- 二分查找
- 算法原理
- 1、二分查找
- 适用题型分析
- 经典题单
- 2、最小完成秒数
- 3、求满足两个数组取数规则最小的最大值
- 4、嗑药的工人能做任务最大数
- 5、第k小数组组合数
- 6、相同硬币组合的第k小组合数
- 7、第k小的乘积
- 8、指定范围内子数组和的和
- 9、第k大的子序列
- 总结
算法原理
先看一张图,重点在于脑海中模拟取值区域:

数值越小越不能满足要求,越大越能满足要求,如果题目求最小的满足要求的值,那就是右侧区间最小的数,即为L,如果题目求最大的满足要求的值,那就是左侧区间最大的数,即为R。
每次取 [L,R] 左右区间的中间节点 (L+R)>>>1 ,如果判定大了,就移动右边界,此时中间节点相当于左移了,变小了,如果判定小了,就移动左边界,此时中间节点相当于右移,即变大了。
如何设定L和R的值,左右边界的值可以带入结果进行思考,思考结果最小可能的取值,最大可能的取值。
对于二分查找,还有一个问题,就是为什么二分的结果就是答案,有没有可能二分的结果不在数组中?
使用反证法,假设我们找的是最大的小于等于num的值,如果存在更小的值满足要求,那二分查找不会停止,如果真正的结果是更大的值,那二分查找时左端点会右移。
在实际做题时可以思考num=真实结果时左右端点移动的情况,结合上面这张图,基本没有二分边界的问题。
下面给出二分查找的java版本代码,其他语言如果有二分查找的库函数,例如Python和Golang,在清楚函数使用方法后也可以用,但是对于初学者容易搞蒙。
1、二分查找
要求在非递减数组中返回最小满足nums[i]>=target的i,如果不存在就返回n
左闭右闭区间 [left, right]
最后right+1是left,是满足nums[i]>=target的区间,而left-1是恰好不满足要求的区间
while (left <= right) { // 区间不为空
// 循环不变量:
// nums[left-1] < target
// nums[right+1] >= target
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1; // 范围缩小到 [mid+1, right]
} else {
right = mid - 1; // 范围缩小到 [left, mid-1]
}
}
左闭右开区间 [left, right)
while (left < right) { // 区间不为空
// 循环不变量:
// nums[left-1] < target
// nums[right] >= target
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1; // 范围缩小到 [mid+1, right)
} else {
right = mid; // 范围缩小到 [left, mid)
}
}
左开右开区间 (left, right)
while (left + 1 < right) { // 区间不为空
// 循环不变量:
// nums[left] < target
// nums[right] >= target
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid; // 范围缩小到 (mid, right)
} else {
right = mid; // 范围缩小到 (left, mid)
}
}
适用题型分析
适合用二分查找解题的题型有:
1、最小、最大
最小/大一类问题容易误判二分做法,如果没有明显的单调性,可以考虑其他做法,例如动态规化。
2、最小的最大值、最大的最小值
这一类问题比较简单,二分特征明显。
3、第K大/小
第k大/小一类问题往往在进行左右边界移动判定时比较困难,总是需要进行小于等于mid的个数是否大于等于k这一类考虑,尤其是和子数组或子序列结合的问题,更是要结合其他解题技巧,例如滑动窗口,前缀和。
在一个需要注意的是,这一类问题用最小堆可能更方便,但是有些数据范围过大,那就只能用二分,二分在处理大范围数据方便往往会有奇效。
二分查找的问题一般难在两点:
1、怎么判断这道题需要用二分解决,解决误判一方面只能靠多刷题,找找感觉,另一方面如果一道题有递增递减的性质,或者在知道一个有单增性的前提条件下能更容易的解决问题,那就可以考虑用二分查找,但是有的问题需要绕一个弯才能发现递增递减,例如第9题。
2、不知道怎么写判定函数,解题技巧的问题一般发生在判定挪移左边界还是右边界的时候,这个时候总要结合其他技巧辅助解题,例如滑动窗口,数组前缀和,位运算,递归,记忆化搜索等等。这就只能靠积累了。
总结一句话:菜就多练
经典题单
2、最小完成秒数
原题速递
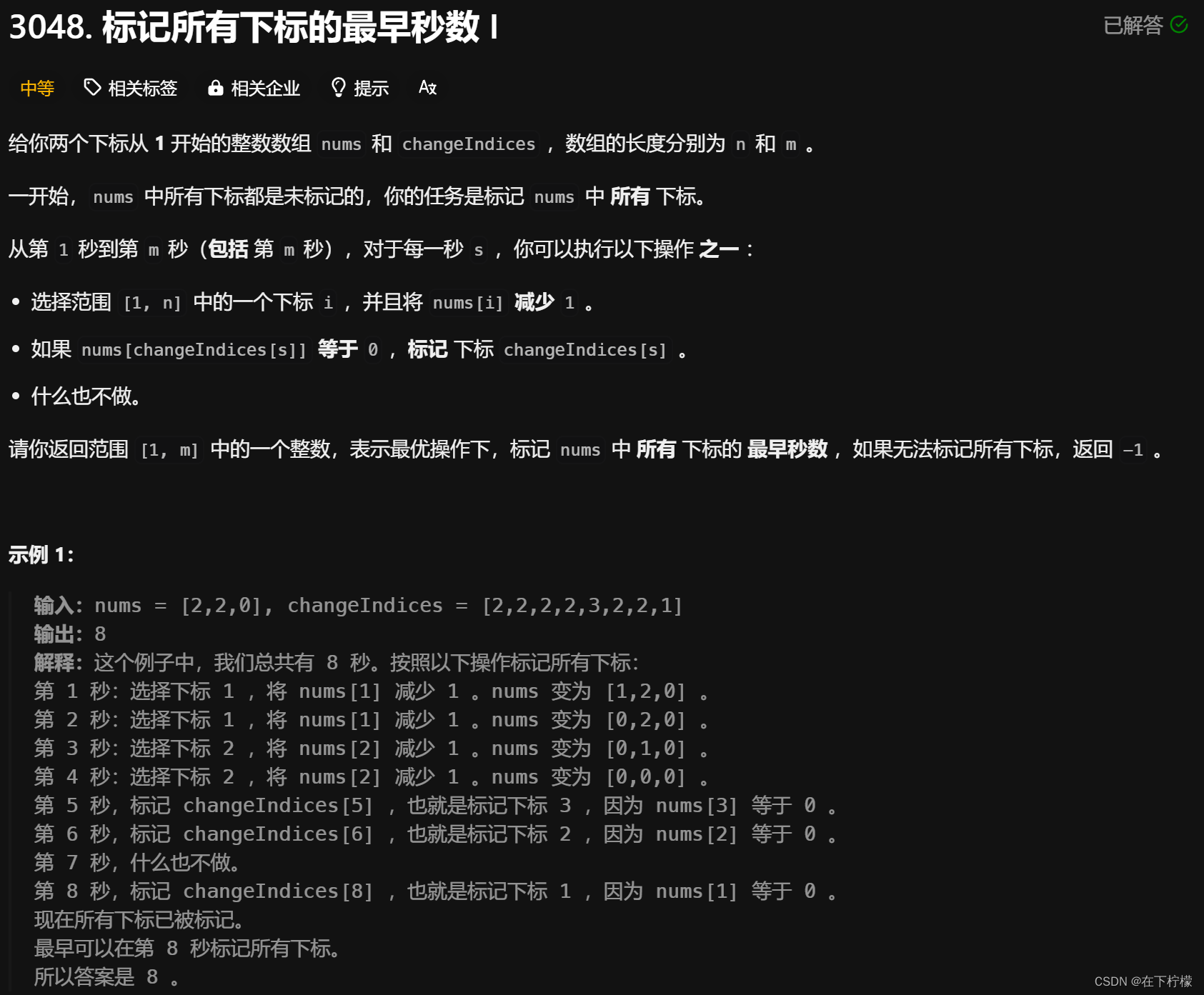
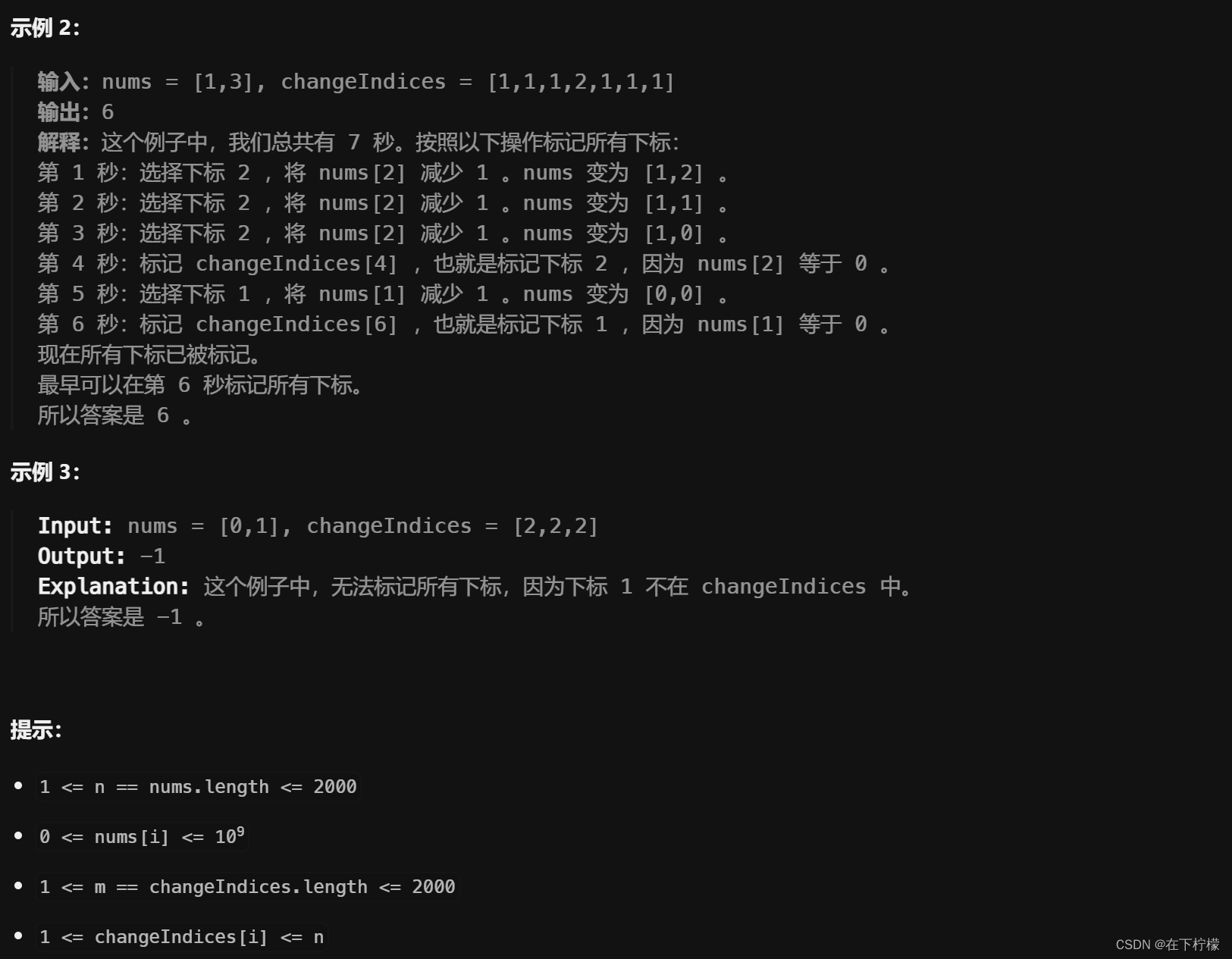
- 翻译一下题目,nums是每门课需要复习的天数,change是每天可以考试的科目
- 完成时间越多,完成概率越大,所以可以二分
- 需要在每门最后一次考试之前完成复习,遍历,在最后一次考试时检查是否有时间复习
- 这个题目的难点在于看出用二分,以及check函数的写法
class Solution {
int[] nums;
int[] changeIndices;
public int earliestSecondToMarkIndices(int[] nums, int[] changeIndices) {
// nums是每门课需要复习的天数,change是每天可以考试的科目
// 完成时间越多,完成概率越大,所以可以二分
// 需要在每门最后一次考试之前完成复习,遍历,在最后一次考试时检查是否有时间复习
this.nums = nums;
this.changeIndices = changeIndices;
int n = changeIndices.length;
int l = 1, r = n;
while (l<=r){
int m = (l+r)>>>1;
if (check(m)) r = m-1;
else l = m+1;
// System.out.println(l+":"+r);
}
return l<=n && check(l)?l:-1;
}
boolean check(int time){
// 是否能在time时间内完成所有考试,在最后一次考试时检查是否有时间复习
int n = nums.length;
// 预处理下标,得到每门课最后一次考试时间
int[] last = new int[n];
Arrays.fill(last,-1);
for (int i=0;i<time;i++) last[changeIndices[i]-1] = i;
// 是否有的科目考不了试
for (int x : last) if (x==-1) return false;
// 统计考试前能用的时间
int cnt = 0;
for (int i=0;i<time;i++){
int x = changeIndices[i]-1;
if (i==last[x]){
// 这门课最后考试期限
if (cnt<nums[x]) return false;
cnt -= nums[x];
}else{
cnt++;
}
}
return true;
}
}
3、求满足两个数组取数规则最小的最大值
原题速递

- 最大元素是x,[1,x]中整除d2的数只能在arr1中,整除d1的数只能在arr2中,不能整除d1d2的两个数组都可以放
- x越大,越可以选出cnt1和cnt2个数,所以二分
- 对x计算上面三个数字,如果可以满足cnt1和cnt2就修改范围
class Solution {
long LCM = -1;
public int minimizeSet(int d1, int d2, int cnt1, int cnt2) {
// 最大元素是x,[1,x]中整除d2的数只能在arr1中,整除d1的数只能在arr2中,不能整除d1d2的两个数组都可以放
// x越大,越可以选出cnt1和cnt2个数,所以二分
// 对x计算上面三个数字,如果可以满足cnt1和cnt2就修改范围
long l = 1, r = (cnt1+cnt2)*2-1;
// d1d2最小公倍数 = d1*d2/最大公约数
// 这里注意先除后乘,并且转化为long求最大公约数,以免溢出
LCM = d1/gcd(d1,d2)*d2;
while (l<=r){
long m = (l+r)>>>1;
if (check(m,d1,d2,cnt1,cnt2)) r = m-1;
else l = m+1;
}
return (int)l;
}
long gcd(long x, long y){
// 求最大公约数
if (x==0) return y;
return gcd(y%x,x);
}
boolean check(long m, int d1, int d2, int cnt1, int cnt2){
// 是否能从[1,m]中选出cnt1,cnt2个满足要求的数
long share = m/LCM;
long num1 = m/d2-share;
long num2 = m/d1-share;
// 容斥定理
long num3 = m-m/d1-m/d2+share;
// 如果公用的num3不能填补两数差额,就return false
return num3>=Math.max(cnt1-num1,0)+Math.max(cnt2-num2,0);
}
}
4、嗑药的工人能做任务最大数
原题速递
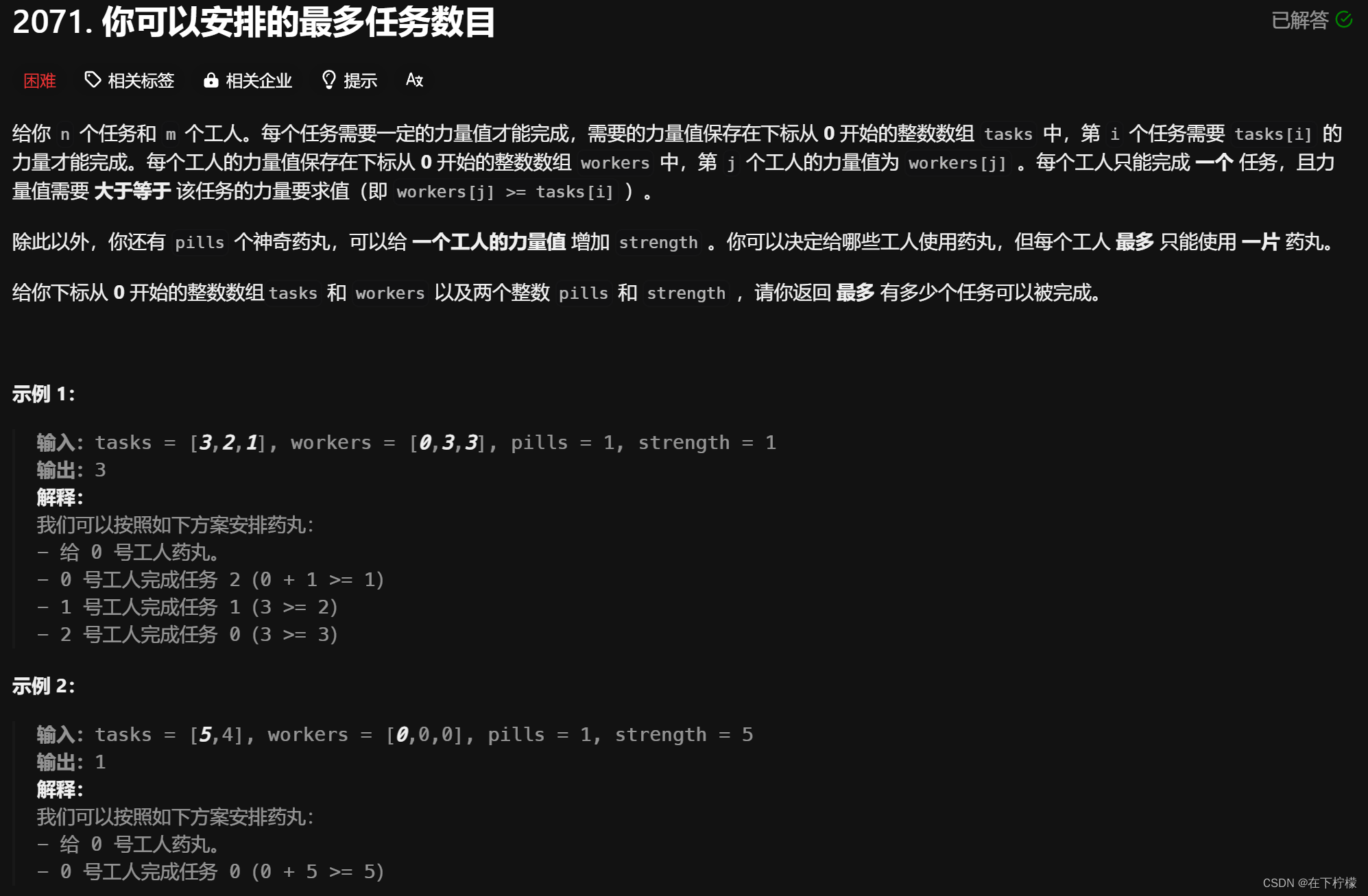
- 二分任务数,难点在于如何确定在能嗑药的情况下是否能做num个任务?
- 要求有num个任务被完成,那肯定是最强壮的num个工人,完成最小的num个任务
- 从大到小枚举任务和工人,如果能做就continue,不能做就让最小的工人吃药丸,从而最大化药丸价值
- 如何找最小工人?遍历到当前任务,只把吃了药丸能做的加入到队列中,这样队列中最小值就是要找的
class Solution {
public int maxTaskAssign(int[] tasks, int[] workers, int pills, int strength) {
// 二分任务数
Arrays.sort(tasks);
Arrays.sort(workers);
int n = Math.min(tasks.length, workers.length);
int l = 0, r = n;
while (l<=r){
int m = (l+r)>>>1;
if (check(tasks,workers,m,pills,strength)) l = m+1;
else r = m-1;
}
return r;
}
boolean check(int[] tasks, int[] workers, int num, int pills, int strength){
// 要求有num个任务被完成,那肯定是最强壮的num个工人,完成最小的num个任务
// 从大到小枚举任务和工人,如果能做就continue,不能做就让最小的工人吃药丸,从而最大化药丸价值
// 如何找最小工人?遍历到当前任务,只把吃了药丸能做的加入到队列中,这样队列中最小值就是要找的
Deque<Integer> q = new ArrayDeque();
int n = workers.length, j = 1;
for (int i=num-1;i>=0;i--){
int t = tasks[i];
// 只把吃了药丸能做的工人加入队列
while (j<=num && workers[n-j]+strength>=t){
q.addLast(workers[n-j]);
j++;
}
// 没人可用
if (q.isEmpty()) return false;
// 最大的能做就做,否则让最小的吃药做,如果药没了就false
if (q.getFirst()>=t) q.removeFirst();
else if (pills-- > 0) q.removeLast();
else return false;
}
return true;
}
}
5、第k小数组组合数
原题速递

- 从每一行中选出一个数,组合成一个新的数组,求第k小的数组和
- 暴力,数据量是 [40×40],所以可以暴力,每一行选出k个最小数,下一行相加,有k×m个组合,选出其中最小的k个,依次遍历
- 二分,数组和越大,数组个数越多,用回溯统计数组和小于mid的个数,如果个数大于等于k就直接返回,但是二分的结果有没有可能不能由组合数得到呢?比如数组中的元素都是偶数,但是二分算出来的却是奇数,我们二分得到的是组合个数大于等于k的最小的数组和,注意这个最小,最后的结果只能是数组中的组合,不可能大于1或者小于1
- 最小堆,本质还是暴力,在暴力中我们用数组来维护每一层的最小的k个数组和,现在可以用最小堆来计算维护数组和当前数组这两个数组的最小的前k个最小和
暴力:
class Solution {
public int kthSmallest(int[][] mat, int k) {
// 每行维护k个最小值,下一行m个数与这k个数相加维护前k个最小值,依次遍历
int n = mat.length, m = mat[0].length;
int[] nums = new int[]{0};
for (int i=0;i<n;i++){
int[] arr = new int[nums.length*m];
int idx = 0;
for (int pre : nums){
for (int x : mat[i]){
arr[idx++] = pre+x;
}
}
Arrays.sort(arr);
nums = Arrays.copyOfRange(arr,0,Math.min(k,arr.length));
}
return nums[k-1];
}
}
二分:
这里需要注意一点,正常的递归是超时的,即便有剪枝优化,但还不够,还需要加上一点优化。
让sum减去第一列的和,如果当前sum小于0,就说明剩下即便每层选最小数仍然选不出新数组,进行剪枝操作。
正常的递归是,选一个数直接从sum减去即可,现在需要加上每一行最小值,再减去当前选择得数
加上这个优化就能不超时了。
class Solution {
int k;
int offset;
public int kthSmallest(int[][] mat, int k) {
// 二分数组和
int n = mat.length, m = mat[0].length, sum0 = 0, sum1 = 0;
for (int i=0;i<n;i++){
sum0 += mat[i][0];
sum1 += mat[i][m-1];
}
offset = n;
int l = sum0, r = sum1;
while (l<=r){
int mid = (l+r)>>>1;
this.k = k;
if (dfs(n-1,mid-sum0,mat)) r = mid-1;
else l = mid+1;
}
return Math.min(l,sum1);
}
boolean dfs(int i, int sum, int[][] nums){
// 递归统计数组和小于等于sum的个数,如果大于等于k就return true
// 在每一行中枚举元素是否可以选,如果大于数组和,就break剪枝
// 正常的递归是超时的,需要加上一点优化,让sum减去第一列的和,如果当前sum小于0,就说明剩下即便每层选最小数仍然选不出新数组,进行剪枝操作
// 正常来说,选一个数直接从sum减去即可,现在需要加上每一行最小值,再减去当前选择得数
if (i<0) return --k==0;
for (int x : nums[i]){
if (x>sum+nums[i][0]) break;
if (dfs(i-1,sum+nums[i][0]-x,nums)) return true;
}
return false;
}
}
最小堆:
class Solution {
public int kthSmallest(int[][] mat, int k) {
// 最小堆,每一层实际上是nums和mat[i]选出前k个最小的和,可以用最小堆做
int n = mat.length;
int[] nums = new int[]{0};
for (int i=0;i<n;i++){
// 从nums和mat[i]选出前k个最小和
nums = cal(nums,mat[i],k);
}
return nums[k-1];
}
int[] cal(int[] a, int[] b, int k){
int n = a.length, m = b.length;
int len = Math.min(k,n*m), idx = 0;
int[] res = new int[len];
PriorityQueue<int[]> q = new PriorityQueue<int[]>((a1,a2) -> (a1[0]-a2[0]));
q.add(new int[]{a[0]+b[0],0,0});
for (int i=0;i<len;i++){
int[] c = q.poll();
res[idx++] = c[0];
int x = c[1], y = c[2];
if (y==0 && x+1<n) q.offer(new int[]{a[x+1]+b[0],x+1,0});
if (y+1<m) q.offer(new int[]{a[x]+b[y+1],x,y+1});
}
return res;
}
}
6、相同硬币组合的第k小组合数
原题速递

- 二分,但是怎么统计num是第几小的数呢?如果只有3个数,很好统计,
a+b+c-ab-ac-bc+abc - 但是对于n的范围是[1,25],如何去重,还能用容斥定理吗?
- 对于更一般的容斥定理,一个大小为size的集合,他对结果的贡献是
(-1)^(size-1)*(num/lcm) - 累加所有非空子集的贡献,就是num第几小的数,我们可以预处理所有子集的lcm
- 数组长度最长为15,所以我们用二进制01表示是否选这个数,枚举[0,1<<n)即可遍历所有子集
- 优化,对于下标为i的元素,加入之前的旧子集中组成新的子集,通过或的方式计算子集的下标
class Solution {
public long findKthSmallest(int[] coins, int k) {
// 二分,但是怎么统计num是第几小的数呢?如果只有3个数,很好统计,a+b+c-ab-ac-bc+abc
// 但是对于n的范围是[1,25],如何去重,还能用容斥定理吗?
// 对于更一般的容斥定理,一个大小为size的集合,他对结果的贡献是(-1)^(size-1)*(num/lcm)
// 累加所有非空子集的贡献,就是num第几小的数,我们可以预处理所有子集的lcm
// 数组长度最长为15,所以我们用二进制01表示是否选这个数,枚举[0,1<<n)即可遍历所有子集
// 优化,对于下标为i的元素,加入之前的旧子集中组成新的子集,通过或的方式计算子集的下标
int n = coins.length;
// 如果全选,就是111...111,开辟大小为1<<n的数组
long[] lcms = new long[1 << n];
// 初始化,全不选的lcm是1
lcms[0] = 1;
for (int i=0;i<n;i++){
// 第i个数与之前的集合进行两两组合可以得到新的集合,此时旧集合是mask,新元素是第i个数
// 则新的集合是 (1<<i)|mask
int bit = 1<<i;
for (int mask=0;mask<bit;mask++){
lcms[mask|bit] = lcm(lcms[mask], coins[i]);
}
}
// 二分
long minv = Long.MAX_VALUE;
for (int x : coins) minv = Math.min(minv,x);
long l = minv, r = minv*k;
while (l<=r){
long mid = (l+r)>>>1;
if (check(mid,lcms,n,k)) r = mid-1;
else l = mid+1;
}
return Math.min(l,minv*k);
}
long lcm(long a, long b){
return a*b/gcd(a,b);
}
long gcd(long a, long b){
if (a==0) return b;
return gcd(b%a,a);
}
boolean check(long num,long[] lcms,int n, int k){
// 统计小于等于num的个数,如果大于等于k就true,否则false
long cnt = 0;
for (int i=1;i<(1<<n);i++){
if (Integer.bitCount(i)%2==1){
// 奇数个1,选了奇数个数,加号
cnt += num/lcms[i];
}else{
cnt -= num/lcms[i];
}
}
return cnt>=k;
}
}
7、第k小的乘积
原题速递
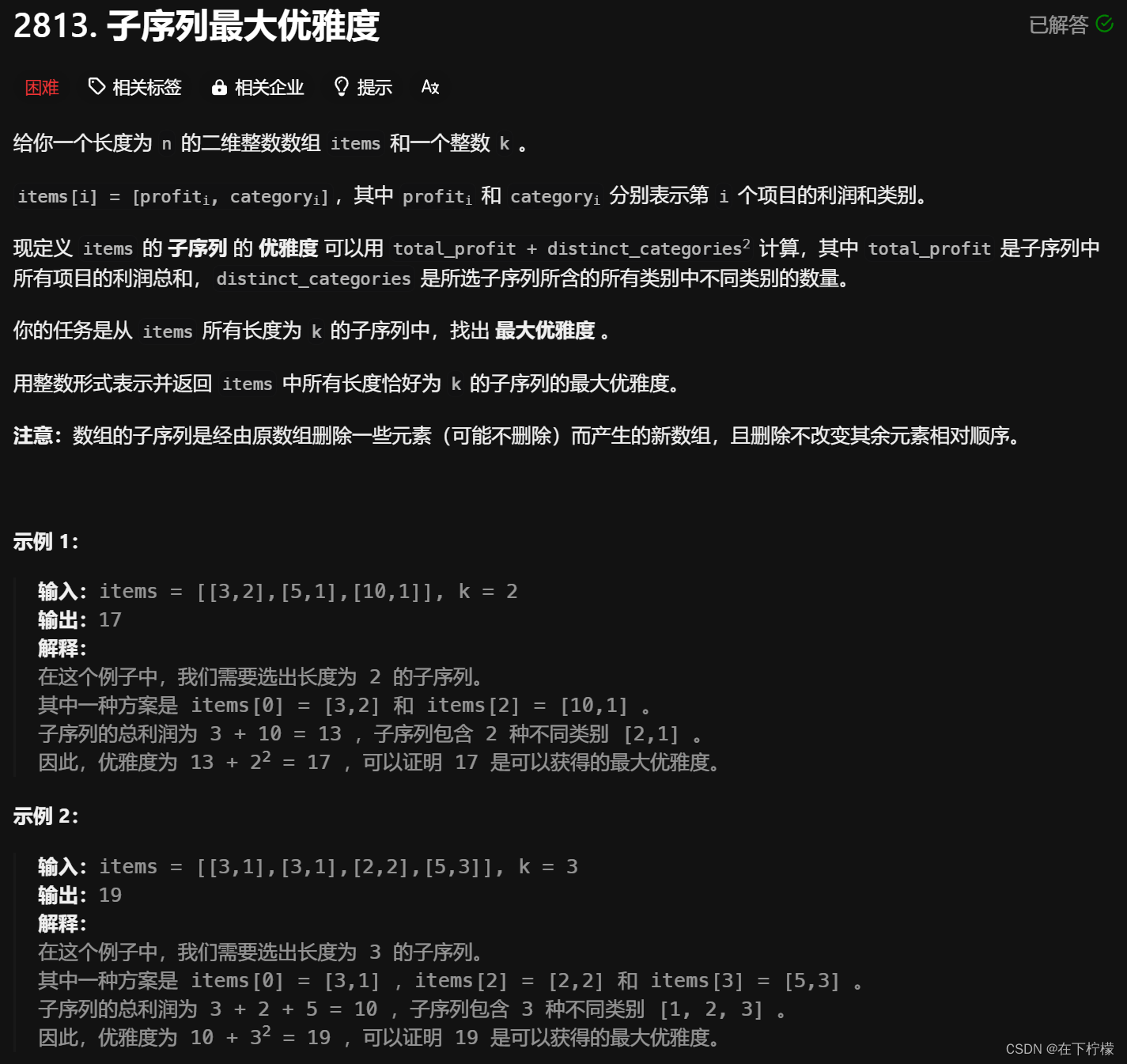
- 数组的范围太大,最小堆预计超时,25e8,那就用二分
- 如果只有正数,那很简单,遍历数组一,找数组二中小于除数的个数
- 但是存在负数,所以要分类讨论,首先计算所有乘积在负数,0,正数的个数
- 例如[-4,-2,0,3],[2,4],6,负数乘积四个,0有两个,正数乘积两个,6=4+2,正好是0
- 如果k小于等于负数,或者大于等于正数,就进行二分
8、指定范围内子数组和的和
原题速递
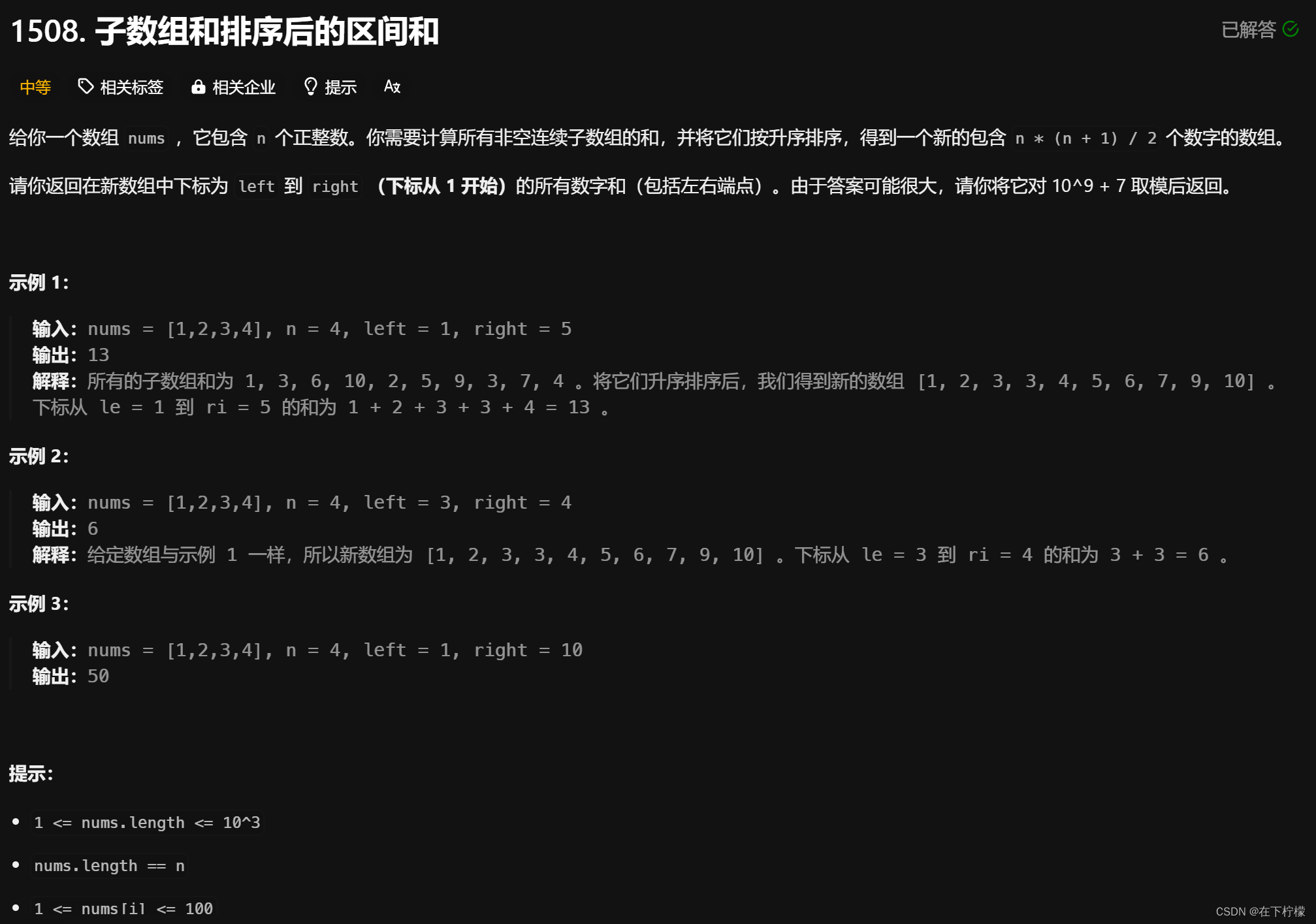
- 暴力做法,求所有n(n+1)/2个子数组的和,排序,求和
[l,r]即可 - 如果能求出最小的r个子数组的和,减去最小的l-1个子数组的和,就得到区间和
- 二分+前缀和求得第k小的子数组的和num
- 通过子数组和的前缀和求得小于num的个数为cnt,并根据前缀和数组求总和sum
- 则等于num的个数为k-cnt,总和=
sum+num*(k-cnt) - 这个算法的关键在于前缀和pre的前缀和prePre,如果前缀和的和prePre符合要求的统计区间在
[i,j],我们直接前缀和的和相减的结果prePre[j]-prePre[i]是会多加一个pre[i]的,需要对每一项减去pre[i],即减去(j-i)*pre[i]
class Solution {
static final int mod = (int)1e9+7;
public int rangeSum(int[] nums, int n, int left, int right) {
// 暴力做法,求所有n(n+1)/2个子数组的和,排序,求和[l,r]即可
// 如果能求出最小的r个子数组的和,减去最小的l-1个子数组的和,就得到区间和
// 二分+前缀和求得第k小的子数组的和num
// 通过子数组和的前缀和求得小于num的个数为cnt,并根据前缀和数组求总和sum
// 则等于num的个数为k-cnt,总和=sum+num*(k-cnt)
// 这个算法的关键在于前缀和的前缀和,
int[] pre = new int[n+1];
for (int i=0;i<n;i++) pre[i+1] = pre[i]+nums[i];
int[] prePre = new int[n+1];
for (int i=0;i<n;i++) prePre[i+1] = prePre[i]+pre[i+1];
return cal(pre,prePre,n,right) - cal(pre,prePre,n,left-1);
}
int cal(int[] pre, int[] prePre, int n, int k){
// 计算前k个最小子数组和的和
// 首先,计算第k小的子数组和
int num = getK(pre,n,k);
// 其次,统计小于num的子数组和的个数
// 遍历i,找prePre[j]<prePre[i]+num的j的个数,累加到cnt上,并维护子数组和的和
int sum = 0, cnt = 0;
for (int i=0, j=1;i<n;i++){
while (j<=n && pre[j]-pre[i]<num){
j++;
}
j--;
cnt += j-i;
// 计算子数组和小于num的和,第一部分前缀相减表示[i,j]结尾的前缀和,每一项都多加了pre[i],需要减去
sum = (sum+prePre[j]-prePre[i]-pre[i]*(j-i))%mod;
}
// 最后,加上等于num的部分,就得到小于等于num的前k个子数组和的和。
sum = (sum+num*(k-cnt))%mod;
return sum;
}
int getK(int[] pre, int n, int k){
// 计算第k小的子数组和
if (k==0) return 0;
int l = 0, r = pre[n];
while (l<=r){
int m = (l+r)>>>1;
if (check(m,pre,n,k)) r = m-1;
else l = m+1;
}
return Math.min(l,pre[n]);
}
boolean check(int num, int[] pre, int n, int k){
// 如果小于等于num的个数大于等于k,就true,否则false
// 遍历i,pre[i]+num>=pre[j],统计j的下标
int cnt = 0;
for (int i=0, j=1;i<n;i++){
while (j<=n && pre[j]-pre[i]<=num){
j++;
}
j--;
cnt += j-i;
if (cnt>=k) return true;
}
return false;
}
}
9、第k大的子序列
原题速递

- 最大的子序列的和=所有正数相加,之后减去正数或者加上负数都会导致和减小,即减去绝对值
- 每次减去最小的绝对值就能得到第k+1大的子序列和,减去的数越多,子序列和越小,有单调性
- 计算正数和sum,在[0,绝对值之和]范围内对子序列和进行二分,dfs找第k小的子序列和,用sum减去即可
class Solution {
public long kSum(int[] nums, int k) {
// 最大的子序列的和=所有正数相加,之后减去正数或者加上负数都会导致和减小,即减去绝对值
// 每次减去最小的绝对值就能得到第k+1大的子序列和,减去的数越多,子序列和越小,有单调性
// 计算正数和sum,在[0,绝对值之和]范围内对子序列和进行二分,dfs找第k小的子序列和,用sum减去即可
long sum = 0, maxAbs = 0;
int n = nums.length;
for (int i=0;i<n;i++){
if (nums[i]>=0) sum += nums[i];
else nums[i] = -nums[i];
maxAbs += nums[i];
}
Arrays.sort(nums);
long l = 0, r = maxAbs;
while (l<=r){
long m = (l+r)>>>1;
// 选或不选递归统计子序列,如果选了,就是一个合法子序列,cnt++
// cnt反向递归,如果为0,就判定为true,首先排除空子序列这种情况
cnt = k-1;
dfs(0,nums,m);
// 如果小于等于m的子序列的个数大于等于k,就移动右边界
if (cnt==0) r = m-1;
else l = m+1;
}
return sum-Math.min(l,maxAbs);
}
int cnt;
void dfs(int i, int[] nums, long sum){
if (i==nums.length || sum<nums[i] || cnt==0) return;
// 选
cnt--;
dfs(i+1,nums,sum-nums[i]);
// 不选
dfs(i+1,nums,sum);
}
}
总结
在刷完题单后依然感觉面对较难的题目无从下手,我的猜测是两方面原因
一方面,算法题是需要积累的,这是一个过程,可能是长时间的苦练,也可能是一时的开窍
另一方面,解题是多方面的,而非单个二分查找可以以偏概全,需要积累技巧和解题思路。
总之,还得努力。