目录
1、顺序表
2、随机访问&顺序访问
3、思考
4、顺序表的封装
1、顺序表
数组在数据结构中是属于线性表的一种,线性表是由一组具有n个相同类型的数据元素组成的。线性表中的任何一个数据元素
- 有且只有一个直接前驱
- 有且只有一个直接后继
- 首元素是没有前驱的
- 尾元素是没有后继的

- 某个元素的左侧相邻元素被称为“直接前驱”,
- 元素左侧所有的数据元素被称为“前驱元素”。
- 某个元素的右侧相邻元素被称为“直接后继”,
- 元素右侧所有的数据元素被称为“后继元素”。

满足这种数学关系的一组元素,逻辑关系就是线性结构,并且逻辑关系是一对一的,比如一个教室学生的学号、一个排队的队伍、一摞堆好的盘子.....都属于线性结构,当然线性结构和存储方式是无关的,简单理解:只有逻辑关系是一对一的,就是线性结构。
所以,根据数据的存储方式可以把线性表分为两种
- 顺序存储的线性表
- 链式存储的线性表。
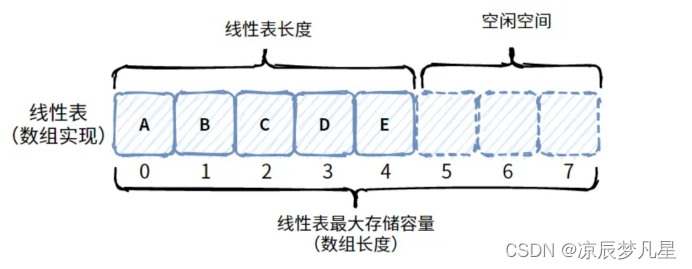
顺序表指的是使用一组内存地址连续的内存单元来依次存储线性表中的数据元素,使用这种存储结构的线性表就被称为顺序表。
简单理解:数据存储在一块连续的内存中,在C语言中可以具名的数组,也可以使用匿名的数组(堆内存)。
顺序表的特点:数据元素之间的逻辑关系是相邻的,并且内存地址也是相邻的,所以只要知道存储线性表的第一个数据元素的内存地址,就可以对线性表中的任意一个元素进行随机访问。通常用户使用动态分配的数组来实现顺序表,也就是使用堆内存实现。
2、随机访问&顺序访问
随机访问指的是在同等时间内具有访问任意元素的能力
- 随机访问相对立的就是顺序访问
- 顺序访问花费的时间要高于随机访问
比如卷轴(顺序)和书籍(随机)、磁带(顺序)和唱片(随机)。
3、思考
思考:既然数组可以作为线性表来使用,请问如何对数组中的元素进行增加和删除以及访问?
回答:如果打算使用数组实现线性表的特性,需要知道三个条件:
- 数组首元素地址address;
- 数组元素的容量size;
- 数组中元素的个数count。
4、顺序表的封装
#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
//设计数据元素类型
typedef int ElemType;
// 设计一个顺序表节点结构体
struct Sqlist
{
ElemType *data; // 保存数据首地址
int count; // 保存存储的数据个数
int size; // 保存容量
};
// 创建一个顺序表
struct Sqlist *createSq(int size);
// 销毁顺序表
void destroySq(struct Sqlist *sq);
// 在指定位置插入数据
bool insertSq(struct Sqlist *sq, ElemType data, int pos);
// 查询数据--返回数据位置,没找到返回-1
int indexSq(struct Sqlist *sq, ElemType data);
// 删除数据
bool deleteSq(struct Sqlist *sq, ElemType data);
// 遍历显示
void displaySq(struct Sqlist *sq);
// 创建一个顺序表
struct Sqlist *createSq(int size)
{
// 1.申请结构体空间
struct Sqlist *sq = (struct Sqlist *)malloc(sizeof(struct Sqlist));
if (sq == NULL)
{
return NULL;
}
// 2.初始化结构体成员,
sq->size = size;
sq->count = 0;
// 3.申请数据空间
sq->data = malloc(sizeof(ElemType)*(sq->size));
if (sq->data == NULL)
{
// 数据空间申请失败,则将其结构体空间释放
free(sq);
return NULL;
}
// 4.返回结构体指针
return sq;
}
// 销毁顺序表
void destroySq(struct Sqlist *sq)
{
if (sq == NULL)
{
return;
}
// 1.释放数据空间
free(sq->data);
// 2.释放结构体空间
free(sq);
}
// 在指定位置插入数据
bool insertSq(struct Sqlist *sq, ElemType data, int pos)
{
// 1.判断sq是否为空,count与size是否相等(满)
if (sq == NULL)
{
perror("顺序表为NULL");
return false;
}
if (sq->count == sq->size || pos < 0)
{
perror("顺序表满");
return false;
}
// 2.判断pos是否在0-count中间,那么就要进行挪位,如果不在0-count中间就直接插入末尾
if (pos >= sq->count)
{
sq->data[sq->count] = data;
sq->count++;
}
else
{
for (int i = sq->count; i > pos; i--)
{
sq->data[i] = sq->data[i - 1];
}
// 3.把数据放在pos位置
sq->data[pos] = data;
// 4.count++
sq->count++;
}
return true;
}
// 查询数据--返回数据位置,没找到返回-1
int indexSq(struct Sqlist *sq, ElemType data)
{
// 遍历数组, 查到就返回数组下标
if (sq == NULL)
{
return -1;
}
for (int i = 0; i < sq->count; i++)
{
if (sq->data[i] == data)
{
return i;
}
}
return -1;
}
// 删除数据
bool deleteSq(struct Sqlist *sq, ElemType data)
{
// 1.调用indexSq查询
int pos = indexSq(sq, data);
if (pos == -1)
{
return false;
}
// 2.挪位删除
for (int i = pos; i < sq->count - 1; i++)
{
sq->data[i] = sq->data[i + 1];
}
// 3.count--
sq->count--;
return true;
}
// 遍历显示
void displaySq(struct Sqlist *sq)
{
// 遍历数组输出
if (sq == NULL)
{
return;
}
for (int i = 0; i < sq->count; i++)
{
printf("%d ", sq->data[i]);
}
printf("\n");
}
int main(void)
{
// 创建顺序表
struct Sqlist *sq = createSq(10);
// 插入数据
for (int i = 0; i < 11; i++)
{
int data = random() % 100;
insertSq(sq, data, i);
}
// 显示
displaySq(sq);
// 销毁
destroySq(sq);
}