5.1 网络中的树

第一关 认识树

相关知识

一个包含N个节点的连通图G至少含有N-1条边，如果这个连通图恰好只有N-1条边，那么这个图就可以看做是最简单的连通图，我们称之为树（tree）。一个包含了N个节点的无向图G称为一棵树，当且仅当它满足如下任意一个条件：

• 图G是连通的并且有N-1条边；
• 图G是连通的并且不包含圈；
• 图G不包含圈并且有N-1条边；
• 图G中任意两个顶点之间有且仅有一条路径
• 图G中任意一条边都是桥，即去掉图G中任意一条边都会使图变得不连通

编程要求

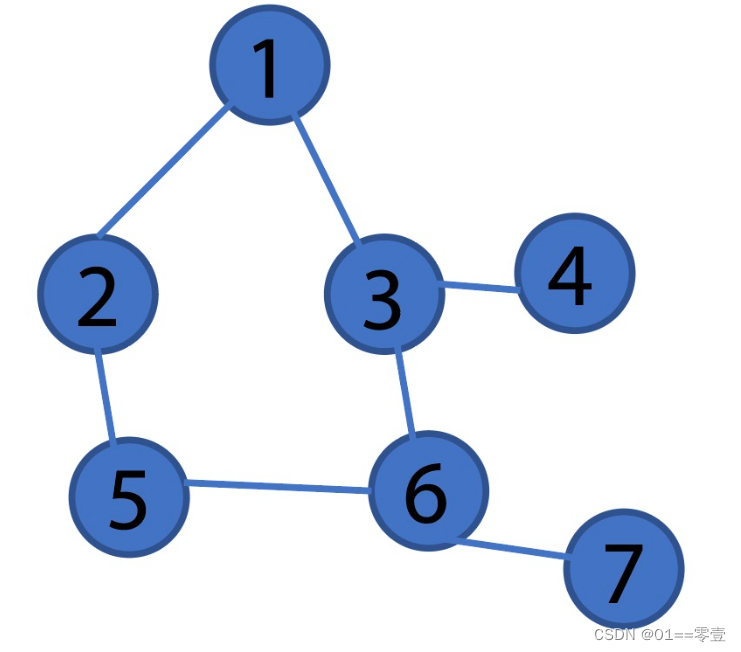
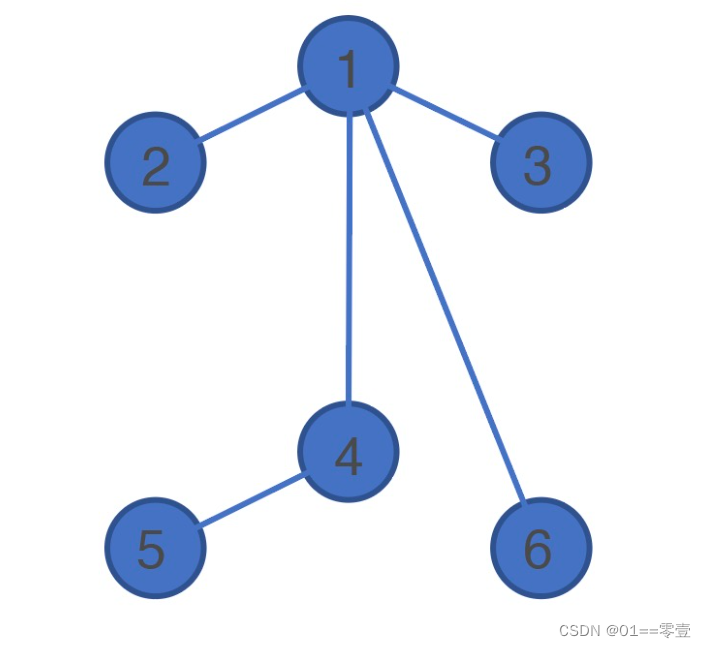
• 根据下图所示的树型网络，理清节点间连接关系及其方向权重信息；
• 再将对应的邻接矩阵G、邻接链表edges以及关联矩阵M在程序空白处输入，元素间请以空格作为间隔；
• 将得到的邻接矩阵G、邻接链表edges以及关联矩阵M由disp命令完成。

代码文件

%Output the G, edges and M, respectively.
G = [0 1 1 1 0 1;1 0 0 0 0 0;1 0 0 0 0 0;1 0 0 0 1 0;0 0 0 1 0 0;1 0 0 0 0 0];
edges = [1 2;1 3;1 4;4 5;1 6];
M = [1 1 1 1 0;1 0 0 0 0;0 1 0 0 0;0 0 1 0 1;0 0 0 0 1;0 0 0 1 0];
disp(G);
disp(edges);
disp(M);

第2关 根节点的二阶邻居求解方法

相关知识

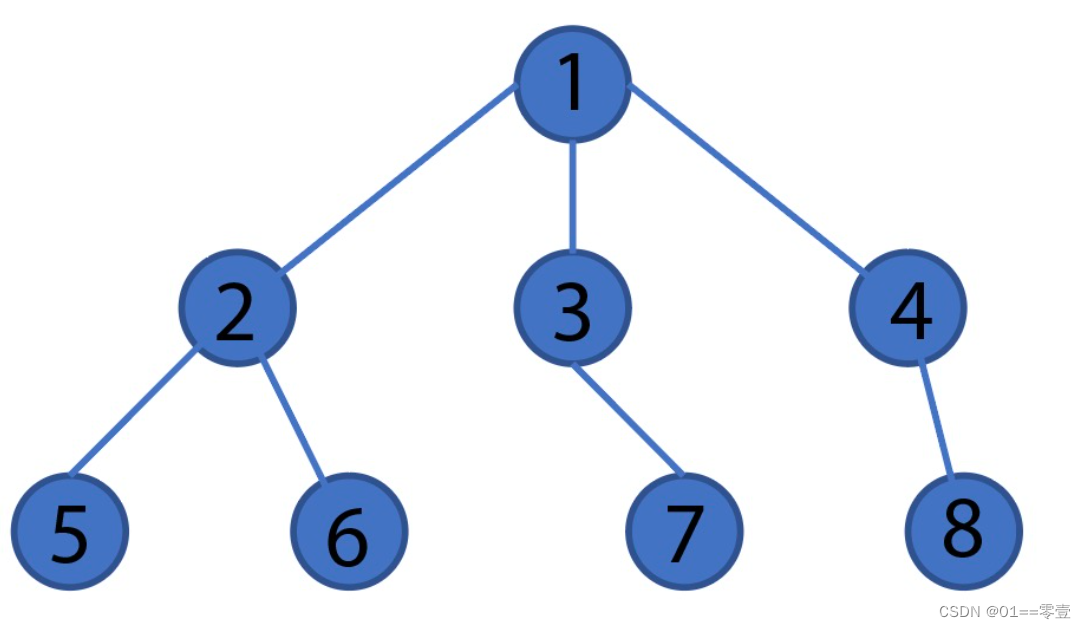
首先在这样一棵树中，我们以节点1作为树的根节点，然后我们每次在向量a中存放已搜索到的根节点邻居，a_temp存放当前搜索到的新邻居。我们知道树的邻接矩阵中非零元素代表节点之间存在连边，那么我们首先定位到邻接矩阵根节点1对应的行，使用find命令找出该行的非零元素位置，并将其存放在向量a_temp中。

a_temp = find(G(1,:));

其中G(1,:)代表邻接矩阵G中第一行的所有元素，利用find命令便可以找出第一行中所有的非零元素的索引值，我们可以看到，根节点1的一阶邻居为节点2，3，4，6。然后我们再以for循环遍历这四个节点的一阶邻居，与根节点一阶邻居不重合的节点便是根节点的2阶邻居。

a = a_temp;
l = length(a_temp);
neighbor = [];
for i = 1:l;
    a_temp = find(G(a(i),:));
    neighbor = union(setdiff(a_temp,a),neighbor);
end

我们首先是求出一阶邻接的数目，然后利用for循环，遍历根节点的每一个一阶邻居，将其二阶邻居节点与已求得的一阶邻居取差集setdiff，便能准确求出专属于二阶邻居的所有节点。

neighbor = setdiff(neighbor,1);
disp(neighbor);

编程要求

代码文件

%Output the neighbor.
G = [0 1 1 1 0 0 0 0;1 0 0 0 1 1 0 0;1 0 0 0 0 0 1 0;1 0 0 0 0 0 0 1;0 1 0 0 0 0 0 0;0 1 0 0 0 0 0 0;0 0 1 0 0 0 0 0;0 0 0 1 0 0 0 0];
a_temp = find(G(1,:));
a = a_temp;
%disp(a_temp); 输出2 3 4
l = length(a_temp);
neighbor = [];
for i = 1:l;
    a_temp = find(G(a(i),:));
    neighbor = union(setdiff(a_temp,a),neighbor);
end
neighbor = setdiff(neighbor,1);
disp(neighbor);

第3关 根节点的n阶邻居求解方法

相关知识

先求出树型网络的二阶邻居，如下所示：

a = a_temp;
l = length(a_temp);%计算根节点一阶邻居的数目
neighbor = [];
for i=1:l
    a_temp = find(G(a(i),:));
    neighbor = union(setdiff(a_temp,a),neighbor);
end

现在讲所求得的邻居节点存入一个临时变量，然后继续遍历二阶邻居的邻居节点，即根节点的三阶邻居，再与临时变量求一个差集即可求得根节点的三阶邻居节点。首先在这样一棵树中，我们以节点1作为树的根节点，然后我们每次在向量a中存放已搜索到的根节点邻居，a_temp存放当前搜索到的新邻居，而不包含前序搜索节点的邻居节点存放在neighbor中。使用find命令找出该行的非零元素位置，并将其存放在向量a_temp中。其中G(a_location(i),:)代表邻接矩阵G中与当前搜索的邻居节点相关的矩阵行中的所有元素，利用find命令便可以找出第一行中所有的非零元素的索引值，然后我们再以for循环遍历这几个节点的一阶邻居，与上一阶节点不重合的节点便是根节点的下一阶阶邻居，求取不重合的节点集我们采用setdiff差集命令，便可最终得到根节点的n阶邻居，如下：

n = 3;%设定根节点的n阶邻居
a = [1];%a为搜索到的节点集合,初始化搜索到的节点集合
a_num = 1;%初始化搜索到的节点数目
neighbor = [];%初始化邻居
k = 1;%循环的控制参数初始化
l = 1;%初始化下一步需要搜索的邻居节点数目
a_location = a;%搜索的定位向量
while k ~= (n+1)
	neighbor = [];
	for i = 1:l
		a_temp = find(G(a_location(i),:));%搜索上一阶邻居的所有相邻节点
		neighbor = union(setdiff(a_temp,a),neighbor);%与当前已搜索到的所有节点取差集,即得到当前阶次的邻居
	end
	a = union(neighbor,a);%更新搜索到的节点集合
	l = length(neighbor);%更新下一步需要搜索的邻居节点数目
	a_location = neighbor;%更新定位向量
	k = k+1;%更新循环的控制参数
end

5.2 权值矩阵与环（无向网络）

第1关 无向网络的权值矩阵

相关知识

编程要求

• 根据下图所示网络图，理清节点间连接关系及其方向权重信息；
• 再将对应的权值矩阵在程序空白处输入，元素间请以空格作为间隔；
• 将得到的权值矩阵由disp命令完成。

代码文件

%Output matrix to A.
A = [0 0 0 0 0;1 0 0 1 0;0 5 0 0 6;0 0 4 0 0;0 0 0 0 0];
disp(A);

第2关 无向网络中环的判定一

相关知识

邻接矩阵每个元素的含义就是如果节点对之间有连边则对应位置的元素值为1，所以我们只需要计算邻接矩阵所有行中非零元素为1的行，便能很快锁定相关节点并进行删除。

sum (G);
a = find(sum(G) == 1);

接下来便是删除操作，如下所示，我们首先计算变量a中节点的数目，利用for循环对选中的节点利用****G(a(i),:)=[]和 G(:,a(i))=[]****指令进行逐一的行列删除。

l=length(a); %如果不止一个节点只含有一条边,求取该类节点的数目
for i=1:l
    G(a(i),:)=[]; %删除节点的对应行
    G(:,a(i))=[]; %删除节点的对应列
end

最后我们再判断是否还有节点只含有一条边，将上面的代码进行整理并加入while循环来控制算法是否终止，因为在实际问题中，网络规模往往很大，所以不可能剥除一次就能将网络中所有只含一条边的节点删除，有可能在一次剥除之后，会产生新的只含一条边的节点，如下图所示，每次循环结束后，用sum计算一次矩阵中是否存在按列求和值为1的节点，如果有则继续进行循环操作，如果没有，则满足算法终止条件，用setdiff差集命令输出环中的节点。

编程要求

• 根据下图所示网络图，理清节点间连接关系及其方向权重信息；
• 再将对应的邻接矩阵矩阵在程序空白处输入，元素间请以空格作为间隔；
• 利用本关卡所学的指令求解网络中环所包含的节点，并存入round；
• 将得到的环中节点由disp命令完成。
  

第3关 无向网络中环的判定二

相关知识

如果一个网络含有环，其总的边数肯定是大于或者等于节点数目，即m>=n，那么我们其实只需要求出网络中的边数与节点数目，便能轻松判定网络中是否存在环。
利用size命令求出网络的尺寸，由于无向网络邻接矩阵是对称矩阵，所以其网络尺寸也就是节点数目，然后利用triu命令求网络的上三角矩阵，再对其整体求和，便能得到边数。我们可以发现边数5=节点数5，说明网络中含环。

编程要求

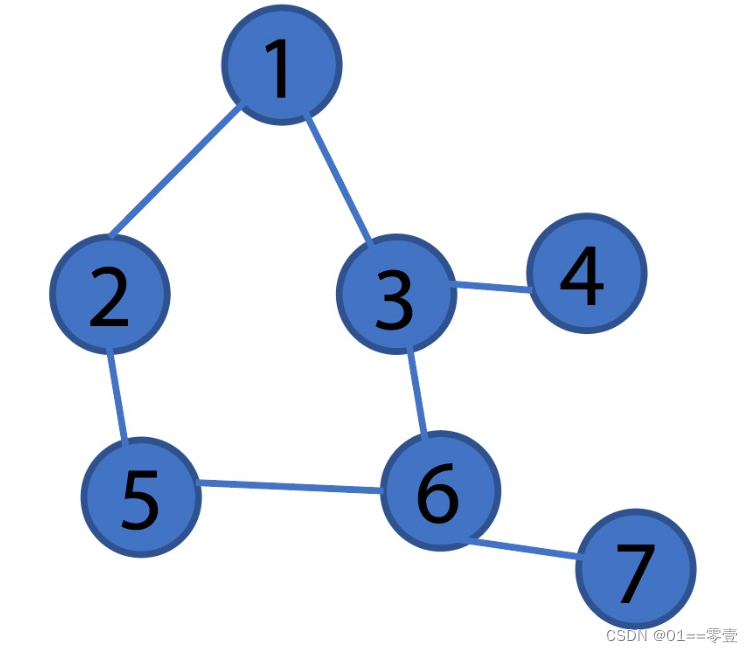
• 根据下图所示网络图，理清节点间连接关系及其方向权重信息；
• 再将对应的邻接矩阵矩阵在程序空白处输入，元素间请以空格作为间隔；
• 利用本关卡所学的指令求解网络中节点与边的数目；
• 利用if语句判断是否存在环，如果存在则输出1，不存在则输出0，并将结果由disp命令输出。

代码文件

A = [0 1 1 0 0 0 0;1 0 0 0 1 0 0;1 0 0 1 0 1 0;0 0 1 0 0 0 0;0 1 0 0 0 1 0;0 0 1 0 1 0 1;0 0 0 0 0 1 0];
n = size(A,1);
A1 = triu(A);
m = sum(A1);
m = sum(m);
if m == n
    disp(1);
end
if m ~= n
    disp(0);
end