目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.背景
2016年,S Mirjalili受到自然界座头鲸社会行为启发,提出了鲸鱼优化算法(Whale Optimization Algorithm, WOA)。


2.算法原理
WOA模拟了座头鲸的社会行为,主要包括包围猎物、随机搜索、螺旋捕猎阶段。

2.1算法思想
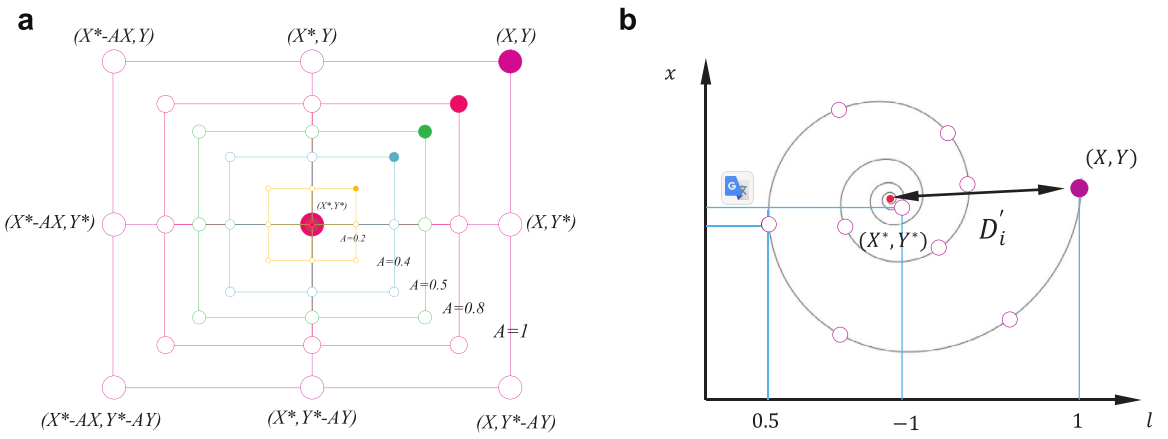
包围猎物
鲸鱼优化算法假设当前种群中最优解为猎物位置或已接近目标猎物的位置,种群中其他鲸鱼个体根据当前最优解更新自身位置:
X
(
i
+
1
)
=
X
b
e
s
t
(
i
)
−
A
⋅
D
(1)
X\left(i+1\right)=X_{best}\left(i\right)-A\cdot D\tag{1}
X(i+1)=Xbest(i)−A⋅D(1)
D为当前鲸鱼与最优解之间的距离:
D
=
∣
C
⋅
X
b
e
s
t
(
i
)
−
X
(
i
)
∣
(2)
D=\begin{vmatrix}C\cdot X_{best}\begin{pmatrix}i\end{pmatrix}-X\begin{pmatrix}i\end{pmatrix}\end{vmatrix}\tag{2}
D=
C⋅Xbest(i)−X(i)
(2)
A和C为搜索控制系数:
A
=
a
(
2
k
−
1
)
C
=
2
k
(3)
\begin{aligned}&A=a\bigl(2k-1\bigr)\\&C=2k \end{aligned}\tag{3}
A=a(2k−1)C=2k(3)
收敛因子:
a
=
2
−
2
i
/
i
max
(4)
a=2-2i / i_{\max}\tag{4}
a=2−2i/imax(4)
随机搜索
鲸鱼种群根据自己当前的位置、全局最优解和一定的随机性来更新自己的位置,使得鲸鱼能够在搜索空间中以一定的概率跳出局部最优解,从而提高搜索到全局最优解的可能性:
X
(
i
+
1
)
=
X
r
a
n
d
(
i
)
−
A
⋅
D
(5)
X\left(i+1\right)=X_{rand}\left(i\right)-A\cdot D\tag{5}
X(i+1)=Xrand(i)−A⋅D(5)
Xrand 为当前进行随机搜索的鲸鱼位置,D表述为:
D
=
∣
C
⋅
X
r
a
n
d
(
i
)
−
X
(
i
)
∣
(6)
D=\left|C\cdot X_{rand}\left(i\right)-X\left(i\right)\right|\tag{6}
D=∣C⋅Xrand(i)−X(i)∣(6)
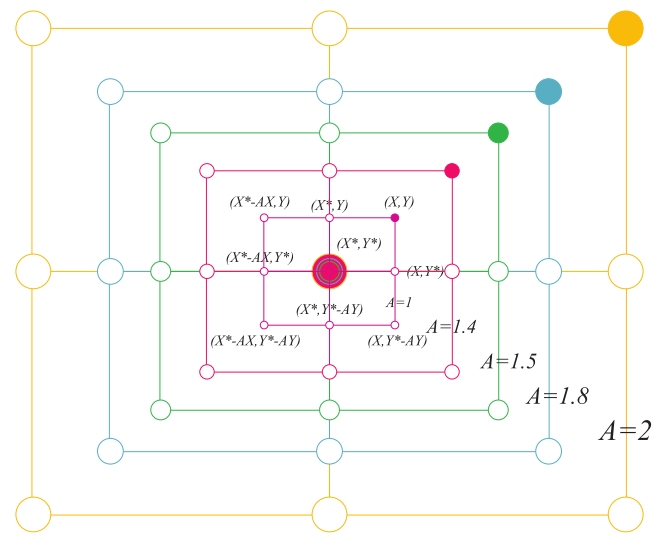
螺旋捕猎
当鲸鱼靠近全局最优解时,它们会以螺旋的方式在局部范围内进行搜索。螺旋行为的策略是在当前位置和全局最优解的位置之间生成一个螺旋路径,然后鲸鱼沿着这个路径进行移动:
X
(
i
+
1
)
=
D
⋅
e
b
l
⋅
cos
(
2
π
l
)
+
X
b
e
s
t
(
i
)
(7)
X\left(i+1\right)=D\cdot e^{bl}\cdot\cos\left(2\pi l\right)+X_{best}\left(i\right)\tag{7}
X(i+1)=D⋅ebl⋅cos(2πl)+Xbest(i)(7)
其中,b 为定义螺旋捕猎的常量系数,l为在[-1,1]随机数,D更新为:
D
=
∣
X
b
e
s
t
(
i
)
−
X
(
i
)
∣
(8)
D=\begin{vmatrix}X_{best}\begin{pmatrix}i\end{pmatrix}-X\begin{pmatrix}i\end{pmatrix}\end{vmatrix}\tag{8}
D=
Xbest(i)−X(i)
(8)
伪代码

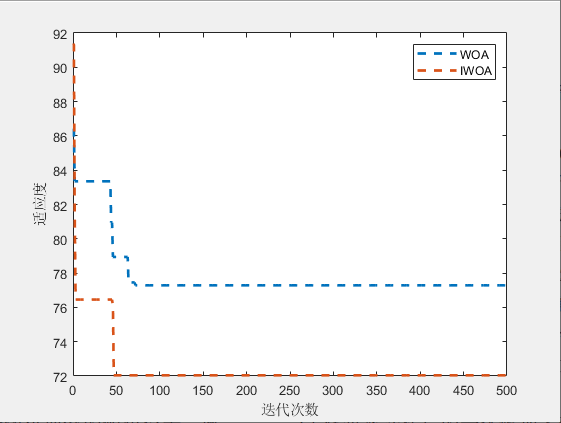
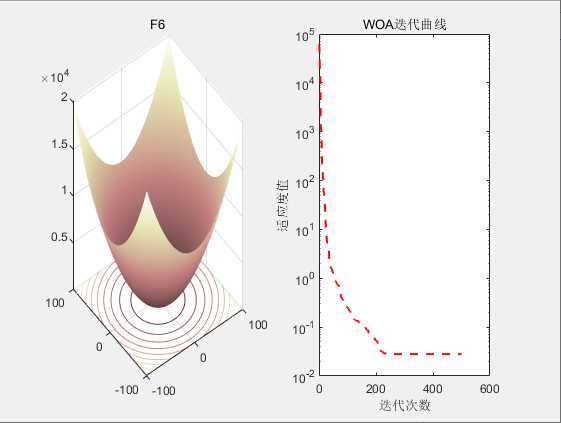
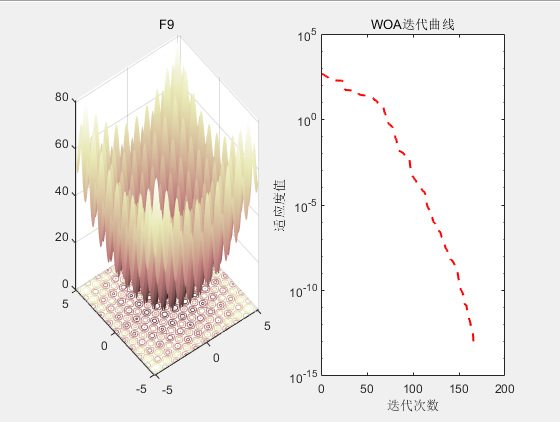
3.结果展示
4.参考文献
[1] Mirjalili S, Lewis A. The whale optimization algorithm[J]. Advances in engineering software, 2016, 95: 51-67.