目录
一、概念
1.1原理分析：
1.2效率分析：
二、模拟实现
2.1位图框架+初始化空间
2.2映射
2.3清零
2.4判断
2.5测试代码
三、位图扩展应用
一、概念
位图，本质上也是一个数组，通过哈希思想构造的一种数据结构，他提现的哈希思想是整数与比特位的映射，通过比特位来代表某种状态，适用于海量数据，数据无重复的场景。通常是用来判断某个数据存不存在。
通过一道经典题来引入如何模拟实现位图结构。
给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。【腾讯】
方法1：遍历，时间复杂度O(N)
方法2：排序O(N*logN)+二分查找O(logN)，时间复杂度O((N+1)*logN)
这两种方法看似都行，但是有一个问题的是40亿个整数大小，每个整形占4个字节，40亿个整数占160亿个字节，而1GB ≈ 10亿个字节，所以40亿个整数≈16GB，而16GB是大于正常的内存大小，我们也无法在内存中开16GB大小的空间。所以，该40亿个数据是存放在文件当中，但是也无法直接导入到内存当中，那么为了解决该问题，就可以采用映射的方式，将数据映射到位图中，且位图的大小是不超过内存的大小。至于原理是什么，接下来进行解释。
方法3：位图
1.1原理分析：
将每个整数想象成一个比特位，对于位图来说，它是个数组，目的就是要将这些整数存储到数组中去，也就是将比特位存储到数组中去，
那么数组存储的数据类型又是什么，只能是整形，如果是char类型，根本存不下，其他类型又不符合，接着将数组中每个整数当成32个比特位去理解，
所以最终目的是将比特位映射到数组中的对应整数中的32个比特位之中，也就是将整数映射到数组中对应整数的32个比特位之中，并将映射位置设为1，所以就可以通过判断映射到32个比特位的对应位置是1或者0来确定该整数是否存在。示意图；
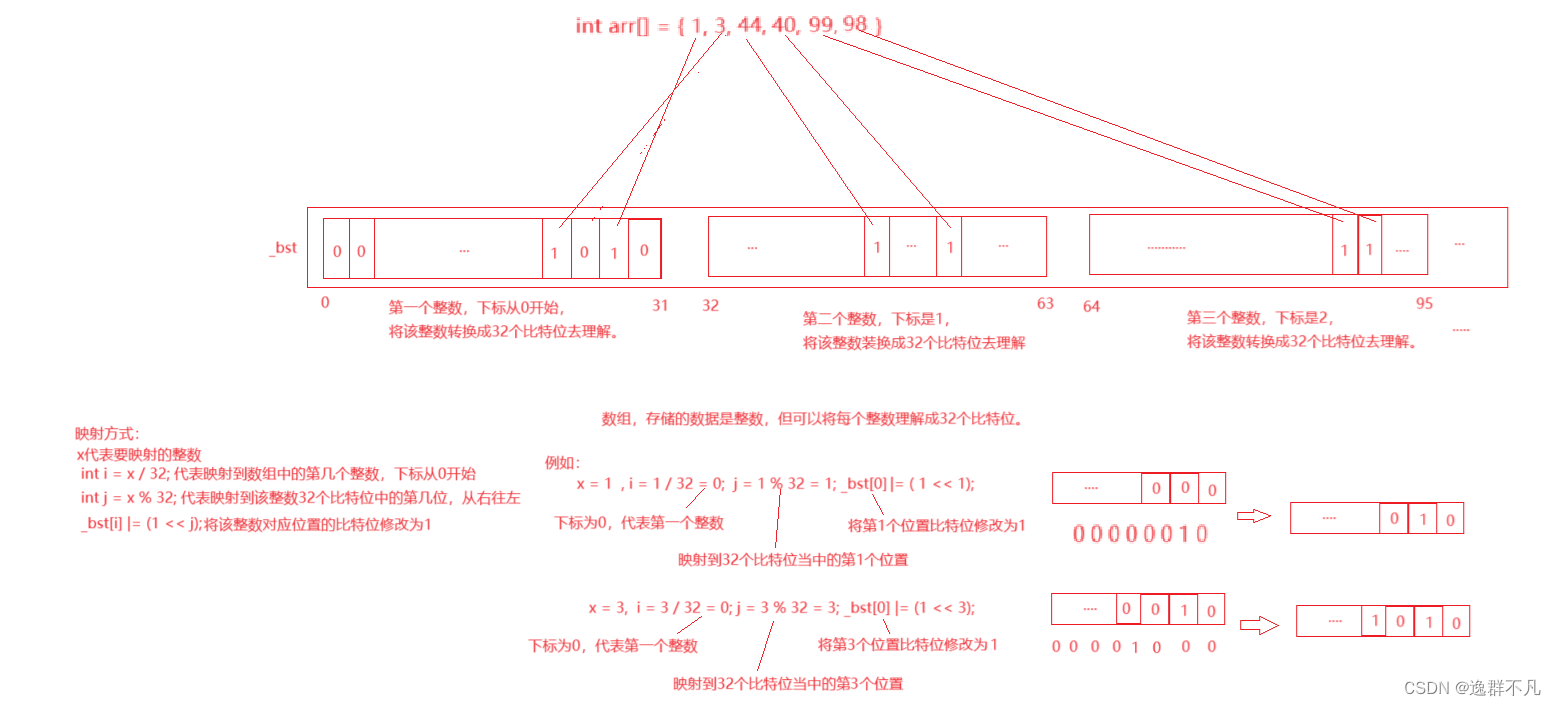通过该图，可以更清晰的了解是如何发生映射的，可以发现，数组中存储的仍然是整数，但是要把整数当成32个比特位去理解，虽然映射后，数组中的整数值是改变了，但是所看的根本就不是该整数值，而是整数对应的比特为是1还是0的状态来判断要映射的整数是否存在。
1.2效率分析：
那么这样算下来，40亿个数据映射到数组中的时间复杂度是O(N),但是对于该16GB的大小，对于数组来说就只要开16GB/32 = 0.5G 大小的空间，且内存是完全够开的，这就是位图体现的作用。
位图就是个以空间换时间的做法，但同时位图有自己的缺陷，就是只能针对整型数据，数据量大，整数在不在的问题。而对于其他数据类型不支持，那么对于这一问题，布隆过滤器可以解决，这在下一章节将解决。
现在就来模拟实现一下位图。
二、模拟实现
2.1位图框架+初始化空间
对于位图，需要容纳海量数据，判断数据是否存在，所以采用的是非类型模板参数。
假设整形个数据个数为N，那么对于位图而言需要开多大空间呢？
是 N/32个吗？ 并不是，对于刚好是32的倍数的确实满足，但对于不能刚好取整的就要多开一个，即使是刚好取整，多开32个比特位空间也不足挂齿。所以最终开的空间是 N/32 + 1个大小空间。
template<size_t N>
class bitset
{
public:
bitset()
{
_bst.resize(N / 32 + 1);
}
private:
vector<int> _bst;
};2.2映射
对于映射，在概念中，也已经简明扼要，这就不在过多阐述。
void set(size_t x)
{
int i = x/32;//在第几个整形
int j = x % 32;//在这个整形的第几个比特位
_bst[i] |= (1 << j);//将该位置设置为1
}2.3清零
对于映射完后的数据，如果不想要了，就可以清理调，那么对此该如何操作了。其实只需要更改一下位操作即可，即_bst[i] &= ~(1<<j);示意图：
实现：
void reset(size_t x)
{
int i = (x >> 5);
int j = x % 32;
_bst[i] &= ~(1 << j);//将对应映射位置清0
}2.4判断
同理只需要更改为操作判断该为是否为1即可
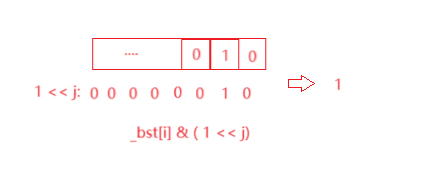
实现：
bool test(size_t x)
{
int i = (x >> 5);
int j = x % 32;
return _bst[i] & (1 << j);//测试该整数映射位置是否为1，即判断整数在不在
}2.5测试代码
//MyBitSet.h
#include <iostream>
#include <vector>
using namespace std;
namespace bit
{
template<size_t N>
class bitset
{
public:
bitset()
{
_bst.resize(N / 32 + 1);
}
void set(size_t x)
{
int i = x/32;//在第几个整形
int j = x % 32;//在这个整形的第几个比特位
_bst[i] |= (1 << j);//将该位置设置为1
}
void reset(size_t x)
{
int i = (x >> 5);
int j = x % 32;
_bst[i] &= ~(1 << j);//将对应映射位置清0
}
bool test(size_t x)
{
int i = (x >> 5);
int j = x % 32;
return _bst[i] & (1 << j);//测试该整数映射位置是否为1，即判断整数在不在
}
private:
vector<int> _bst;
};
}测试：
#include "MyBitSet.h"
int main()
{
bit::bitset<0xffffffff> bst;
int arr[] = { 1,3,7,4,12,16,19,13,22,18 };
for (size_t i = 0; i < sizeof(arr)/sizeof(arr[0]); i++)
{
bst.set(arr[i]);
}
cout << bst.test(7);
return 0;
}输出结果：
三、位图扩展应用
1.给定100亿个整数，设计算法找到只出现一次的整数？
这里直接说解法了，用两个位图来实现，对于这100一个整数可能出现重复的数，那么可以分三种情况，出现0次，1次，2次及以上，那么可以用位图来表示的情况是：
出现0次：0 0
出现1次：0 1
出现2次及以上：1 0，
100亿个整数大约1.25GB,构造两个分别为2GB的位图即可，这样内存开了4GB的空间，也是够的。
代码实现，对于位图的代码，前面已经实现了，这里就直接使用了：
template<size_t N>
class two_bitset
{
public:
void set(size_t x)
{
if (_bst1.test(x) == false && _bst2.test(x) == false)//出现1次
{
_bst2.set(x);
}
else if (_bst1.test(x) == false && _bst2.test(x) == true)//出现2次
{
_bst1.set(x);//1
_bst2.reset(x);//0
}
}
void PrintOnce()
{
for (int i = 0; i < N; i++)
{
if (_bst1.test(i) == false && _bst2.test(i) == true)
{
cout << i << endl;;
}
}
}
private:
bitset<N> _bst1;
bitset<N> _bst2;
};测试：
#include "MyBitSet.h"
int main()
{
bit::two_bitset<100> tbst;
int arr[] = { 1,3,3,7,4,12,12,16,16,19,13,13,22,22,18 };
for (auto e : arr)
{
tbst.set(e);
}
tbst.PrintOnce();
return 0;
}输出结果：
2.给两个文件，分别由100亿个整数，我们只有1G内存，如何找到两个文件交集？
方案一：整型的范围是确定的，如果按大小算大约为2GB，映射到位图中，位图只需开2GB/32 =1/16,所以构造一个位图开0.5G是完全够用的，虽然有100亿个数据，但都脱离不开整型的范围，必然会有重复，且位图会进行去重，所以0.5G必然够用。接着，将一个文件的数据映射到这个位图，再判断另一个文件的数据在不在位图中即可。
方案二：构造两个位图，每个位图开0.5G个内存，分别将两个文件中的数据映射到两个位图中，进行按位与比较即可。
3.1个文件有100亿个整数，1G内存，设计算法找到出现次数不超过2次的所有整数
这跟第一个情况是类似的，分析出现0次，1次，2次，3次及以上，这里就不在实现了。
end~
