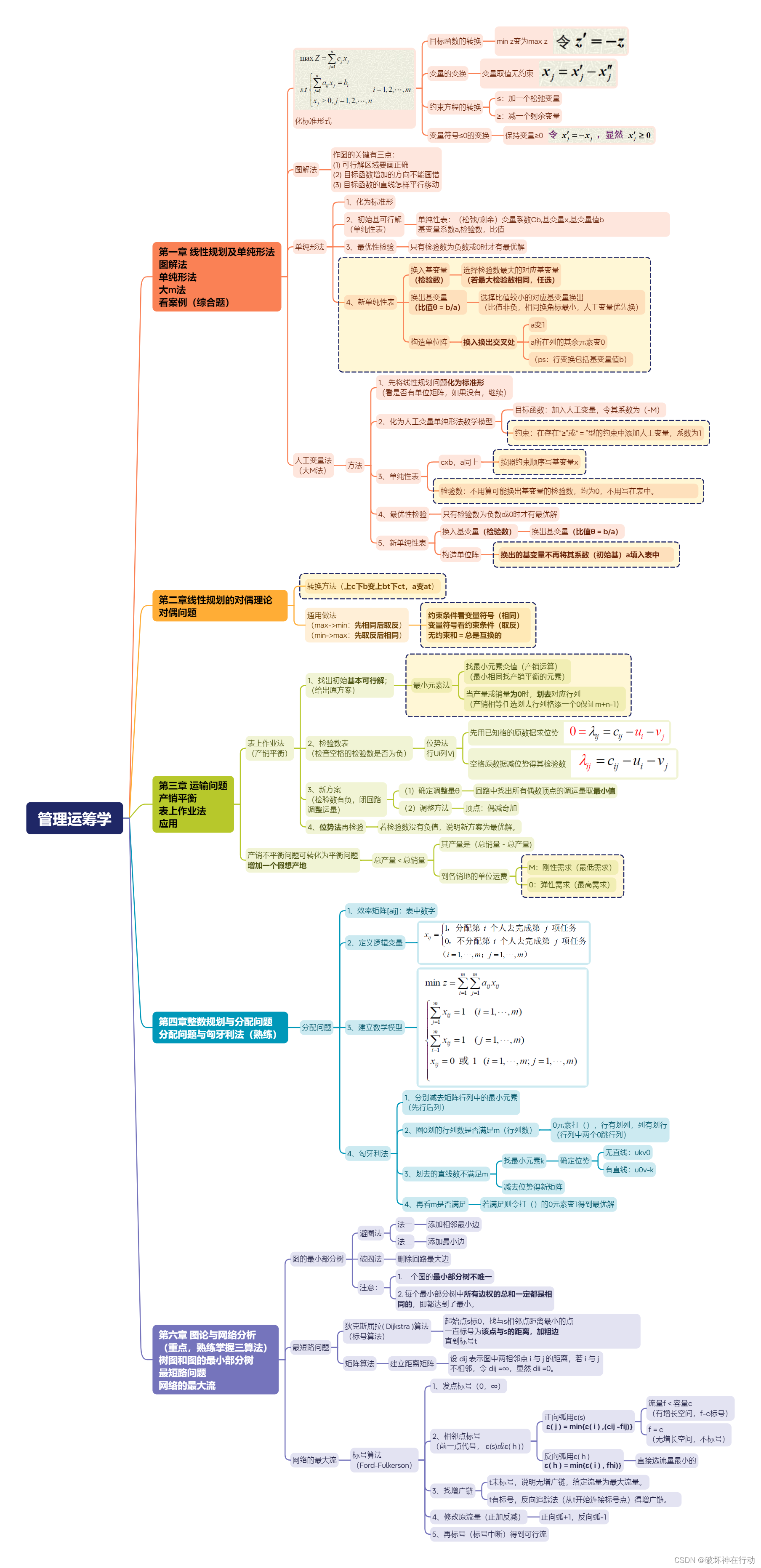
第一章 线性规划及单纯形法

• 图解法 单纯形法 大m法 看案例（综合题）

  • 化标准形式

    • 目标函数的转换

      • min z变为max z

    • 变量的变换

      • 变量取值无约束

    • 约束方程的转换

      • ≤：加一个松弛变量

      • ≥：减一个剩余变量

    • 变量符号≤0的变换

      • 保持变量≥0

  • 图解法

    • 作图的关键有三点：

    • (1) 可行解区域要画正确

    • (2) 目标函数增加的方向不能画错

    • (3) 目标函数的直线怎样平行移动

  • 单纯形法

    • 1、化为标准形

    • 2、初始基可行解 （单纯性表）

      • 单纯性表：（松弛/剩余）变量系数Cb,基变量x,基变量值b 基变量系数a,检验数，比值

    • 3、最优性检验

      • 只有检验数为负数或0时才有最优解

    • 4、新单纯性表

      • 换入基变量 （检验数）

        • 选择检验数最大的对应基变量 （若最大检验数相同，任选）

      • 换出基变量 （比值θ = b/a）

        • 选择比值较小的对应基变量换出 （比值非负，相同换角标最小，人工变量优先换）

      • 构造单位阵

        • 换入换出交叉处

          • a变1

          • a所在列的其余元素变0

          • （ps：行变换包括基变量值b）

  • 人工变量法 （大M法）

    • 方法

      • 1、先将线性规划问题化为标准形 （看是否有单位矩阵，如果没有，继续）

      • 2、化为人工变量单纯形法数学模型

        • 目标函数：加入人工变量，令其系数为（-M）

        • 约束：在存在“≥”或“＝”型的约束中添加人工变量，系数为1

      • 3、单纯性表

        • cxb，a同上

          • 按照约束顺序写基变量x

        • 检验数：不用算可能换出基变量的检验数，均为0，不用写在表中。

      • 4、最优性检验

        • 只有检验数为负数或0时才有最优解

      • 5、新单纯性表

        • 换入基变量（检验数）

          • 换出基变量（比值θ = b/a）

        • 构造单位阵

          • 换出的基变量不再将其系数（初始基）a填入表中

  • 第二章 线性规划的对偶理论

  • 对偶问题

    • 转换方法（上c下b变上bt下ct，a变at）

    • 通用做法 （max->min：先相同后取反） （min->max：先取反后相同）

      • 约束条件看变量符号（相同） 变量符号看约束条件（取反） 无约束和＝总是互换的

  • 第三章 运输问题

  • 产销平衡 表上作业法 应用

    • 表上作业法 （产销平衡）

      • 1、找出初始基本可行解； （给出原方案）

        • 最小元素法

          • 找最小元素变值（产销运算） （最小相同找产销平衡的元素）

          • 当产量或销量为0时，划去对应行列 （产销相等任选划去行列格添一个0保证m+n-1）

      • 2、检验数表 （检查空格的检验数是否为负）

        • 位势法 行Ui列Vj

          • 先用已知格的原数据求位势

          • 空格原数据减位势得其检验数

      • 3、新方案 （检验数有负，闭回路调整运量）

        • （1）确定调整量θ

          • 回路中找出所有偶数顶点的调运量取最小值

        • （2）调整方法

          • 顶点：偶减奇加

      • 4、位势法再检验

        • 若检验数没有负值，说明新方案为最优解。

    • 产销不平衡问题

    • 可转化为平衡问题 增加一个假想产地

      • 总产量＜总销量

        • 其产量是（总销量－总产量)

        • 到各销地的单位运费

          • M：刚性需求（最低需求）

          • 0：弹性需求（最高需求）

  • 第四章 整数规划与分配问题

  • 分配问题与匈牙利法（熟练）

    • 分配问题

      • 1、效率矩阵[aij]：表中数字

      • 2、定义逻辑变量

        • 

      • 3、建立数学模型

        • 

      • 4、匈牙利法

        • 1、分别减去矩阵行列中的最小元素 （先行后列）

        • 2、圈0划的行列数是否满足m（行列数）

          • 0元素打（），行有划列，列有划行 （行列中两个0跳行列）

        • 3、划去的直线数不满足m

          • 找最小元素k

            • 确定位势

              • 无直线：ukv0

              • 有直线：u0v-k

          • 减去位势得新矩阵

        • 4、再看m是否满足

          • 若满足则令打（）的0元素变1得到最优解

  • 第六章 图论与网络分析

  • （重点，熟练掌握三算法） 树图和图的最小部分树 最短路问题 网络的最大流

    • 图的最小部分树

      • 避圈法

        • 法一

          • 添加相邻最小边

        • 法二

          • 添加最小边

      • 破圈法

        • 删除回路最大边

      • 注意：

        • 1. 一个图的最小部分树不唯一

        • 2. 每个最小部分树中所有边权的总和一定都是相同的，即都达到了最小。

    • 最短路问题

      • 狄克斯屈拉( Dijkstra )算法 （标号算法）

        • 起始点s标0，找与s相邻点距离最小的点

        • 一直标号为该点与s的距离，加粗边

        • 直到标号t

      • 矩阵算法

        • 建立距离矩阵

          • 设 dij 表示图中两相邻点 i 与 j 的距离，若 i 与 j 不相邻，令 dij =∞，显然 dii =0。

    • 网络的最大流

      • 标号算法 （Ford-Fulkerson）

        • 1、发点标号（0，∞）

        • 2、相邻点标号 （前一点代号， ε(s)或ε( h )）

          • 正向弧用ε(s) ε( j ) = min{ε( i ) ,(cij -fij)}

            • 流量f＜容量c （有增长空间，f-c标号）

            • f = c （无增长空间，不标号）

          • 反向弧用ε( h ) ε( h ) = min{ε( i ) , fhi)}

            • 直接选流量最小的

        • 3、找增广链

          • t未标号，说明无增广链，给定流量为最大流量。

          • t有标号，反向追踪法（从t开始连接标号点）得增广链。

        • 4、修改原流量（正加反减）

          • 正向弧+1，反向弧-1

        • 5、再标号（标号中断）得到可行流