1.背景
与 Batch normalization 不同,Layer normalization 是在特征维度上进行标准化的,而不是在数据批次维度上。像 Batch Norm 它的核心是数据批次之间的归一化【强调的是第 i 批次和第 i+1 批次的区别,然后BN去缩小他们的的区别】,而 Layer Norm 的核心强调的是每个批次中不同维度数据之间的区别。
2.实现原理
Layer normalization 是在特征维度上进行标准化的,而不是在数据批次维度上。
Layer normalization 的计算可以分为两步:

3.作用
1、特征强化: 通过归一化,每个样本的特征维度被标准化,使得每个维度的数据在训练过程中更加稳定,从而强化了每个维度数据的特征。
2、缓解梯度消失问题: 归一化使得输入数据的均值为零,方差为一,从而使得激活函数的输出更稳定,减小了梯度消失的问题。
3、稳定训练: 由于每一层的输入数据具有相同的均值和方差,梯度的传播更加稳定,有助于训练过程的稳定性和收敛速度。
4、缓解内部协变量偏移: 通过归一化每个样本的特征,Layer Normalization 可以减少每一层输入的分布变化,这有助于缓解训练过程中内部协变量偏移的问题。【虽然没有像BN那样对不同批次相同维的数据进行归一化(BN通过局部批次的数据得到每一个维度上数值的方差和均值),但是因为LN也缩小了数值的大小,所以说分布变化也一定变小了】
5、加速收敛和提高稳定性: 由于输入的均值和方差固定,梯度的变化更为稳定,从而加速了训练过程中的收敛。同时,归一化后的输入有助于缓解梯度消失和梯度爆炸问题,特别是在深层神经网络中。
4.代码
通过一个简单的例子来解释 Layer Normalization (LN) 是如何工作的
import torch
import torch.nn as nn
# 定义一个继承自nn.Module的LayerNorm类
class LayerNorm(nn.Module):
def __init__(self, num_features, eps=1e-6):
super().__init__()
self.gamma = nn.Parameter(torch.ones(num_features)) # 缩放参数γ,可学习,初始值为1
self.beta = nn.Parameter(torch.zeros(num_features)) # 偏移参数β,可学习,初始值为0
self.eps = eps # 防止除以零的小正数
def forward(self, x):
mean = x.mean(dim=-1, keepdim=True) # 计算最后一维的均值
std = x.std(dim=-1, keepdim=True, unbiased=False) # 计算最后一维的标准差
normalized_x = (x - mean) / (std + self.eps) # 归一化处理
return self.gamma * normalized_x + self.beta # 应用可学习的参数并返回结果
if __name__ == '__main__':
batch_size = 2
seqlen = 3
hidden_dim = 4
# 初始化一个随机tensor,模拟一个batch中包含若干序列,每个序列有若干特征的情况
x = torch.randn(batch_size, seqlen, hidden_dim)
print(x)
# 初始化自定义的LayerNorm类
layer_norm = LayerNorm(num_features=hidden_dim)
output_tensor = layer_norm(x) # 对x进行层归一化
print("output after layer norm:\n", output_tensor)
# 使用PyTorch自带的LayerNorm进行对比
torch_layer_norm = torch.nn.LayerNorm(normalized_shape=hidden_dim)
torch_output_tensor = torch_layer_norm(x) # 对x进行层归一化
print("output after torch layer norm:\n", torch_output_tensor)
再举一个简单的例子
虑一个小的输入张量,它代表一个批次中的两个样本,每个样本有两个时间步,每个时间步有三个特征【2,2,3】。我们将使用 Python 和 PyTorch 来演示 LN 的过程:
import torch
# 定义一个小的张量,形状为 [batch_size, time_steps, features]
x = torch.tensor([
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]], # 第一个样本的两个时间步
[[7.0, 8.0, 9.0], [10.0, 11.0, 12.0]] # 第二个样本的两个时间步
])
# 手动实现 Layer Normalization,我们将在每个样本的每个时间步上分别归一化
normalized_x = torch.empty_like(x)
for i in range(x.shape[0]): # 遍历批次
for j in range(x.shape[1]): # 遍历时间步
# 计算第 i 个样本的第 j 个时间步的均值和标准差
mean = x[i, j].mean()
std = x[i, j].std()
# 归一化处理
normalized_x[i, j] = (x[i, j] - mean) / (std + 1e-6)
print("原始数据:")
print(x)
print("归一化后的数据:")
print(normalized_x)
5.LN在Transformer中所放位置
1.PreNorm和PostNorm在公式上的区别:

2.在大模型中的区别:
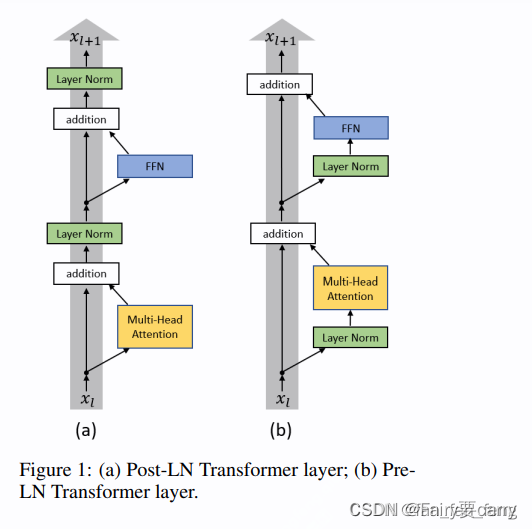
**Post-LN 😗*是在 Transformer 的原始版本中使用的归一化方案。在此方案中,每个子层(例如,自注意力机制或前馈网络)的输出先通过子层自身的操作——>然后再通过层归一化(Layer Normalization)
**Pre-LN:**是先对输入进行层归一化【LN操作】——>然后再传递到子层操作中【自注意力机制+残差】。这样的顺序对于训练更深的网络可能更稳定,因为归一化的输入可以帮助缓解训练过程中的梯度消失和梯度爆炸问题。
残差思想的学习
3.为什么Pre Norm效果比Post Norm效果更好?
我们进行梯度分析:

**总结:**后进行自注意力机制和残差网络,相比之下,能够有效地降低我们的梯度消失风险。


![[大模型]Llama-3-8B-Instruct FastApi 部署调用](https://img-blog.csdnimg.cn/direct/ecbd9a6c64cc43cd9fa170d0e3fb8920.png#pic_center)





![[大模型]LLaMA3-8B-Instruct WebDemo 部署](https://img-blog.csdnimg.cn/direct/41fa668fb76e41548f2e1aec8e8e0a9a.png#pic_center)