LLM Algorithms(1): Flash Attention

news2025/1/16 13:59:04

Background

Flash Attention

Flash Attention Algorithm

参考

NIPS-2022: Flash Attention: Fast and Memory-Efficient Exact Attention with IO-Awareness

idea：减少资源消耗，提升或保持模型性能。
普通attention的空间复杂度是 $O(N^2)$ --》降低到Flash Attention $O(N)$ 。
Exact 结果相等。这不是attention的近似计算，Flash Attention的计算结果和原始方法一致。
IO aware. 和传统attention相比，Flash Attention会考虑硬件特性，而不是把它当作黑盒。

Background

Nvidia GPU (GPU性能指标 = FLOPS / GB/s，FLOPS, GPU计算能力--每秒计算速度；GB/s，GPU内存吞吐量)

2016-P100
2018-V100
2020-A100
2022-H100

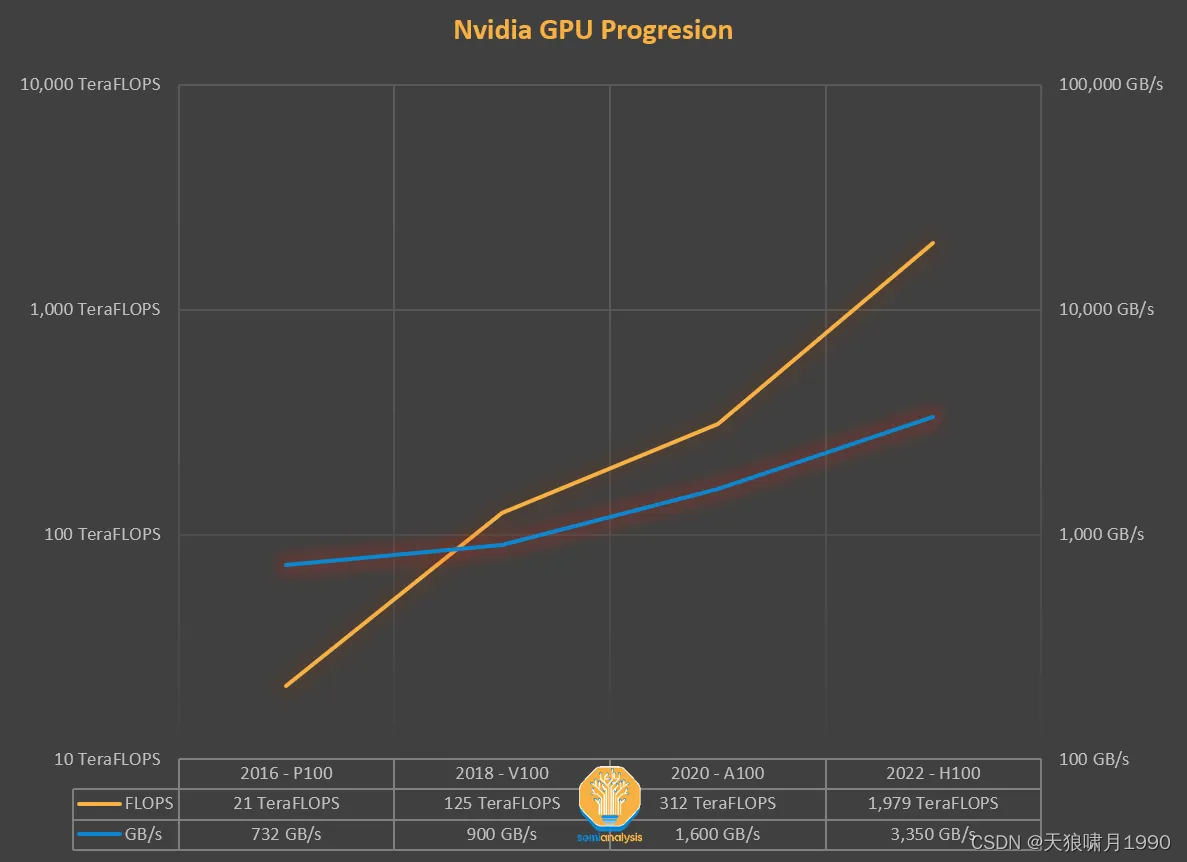
多年来，GPU的计算能力(FLOPS)的增长速度比增加内存吞吐量(TB/s)更快。

这两者需要紧密配合去达到数据处理的最优比，但自从硬件失去了这种平衡，我们必须通过软件来进行补偿。因此需要算法能够感知IO (IO-aware)。根据计算和内存访问比例，一个操作可以分为：

计算受限型 (e.g. 矩阵乘法)
内存受限型
1. Element-wise 逐元素操作: activation, dropout, masking.
2. Reduction 操作: softmax, layer norm, sum.

element-wise操作是指在计算时只依赖当前值，比如每个元素都乘以2。而reduction依赖所有值(比如整个矩阵或矩阵的行)，比如softmax。

attention的计算时内存受限的，因为它的大部分计算都是element-wise的。

尽管masking、softmax和dropout操作占用了大部分时间，但大部分FLOPS都用在矩阵乘法中，虽然他们花的时间不多。即数据太庞大，attention计算内存不足，或者说内存利用效率太低！

可以通过内存调整去加速masking、softmax和dropout这些操作呢，但是具体咋办？

人们都知道把大矩阵切分成小块，但如何保证切分小块的计算结果=原attention计算结果？

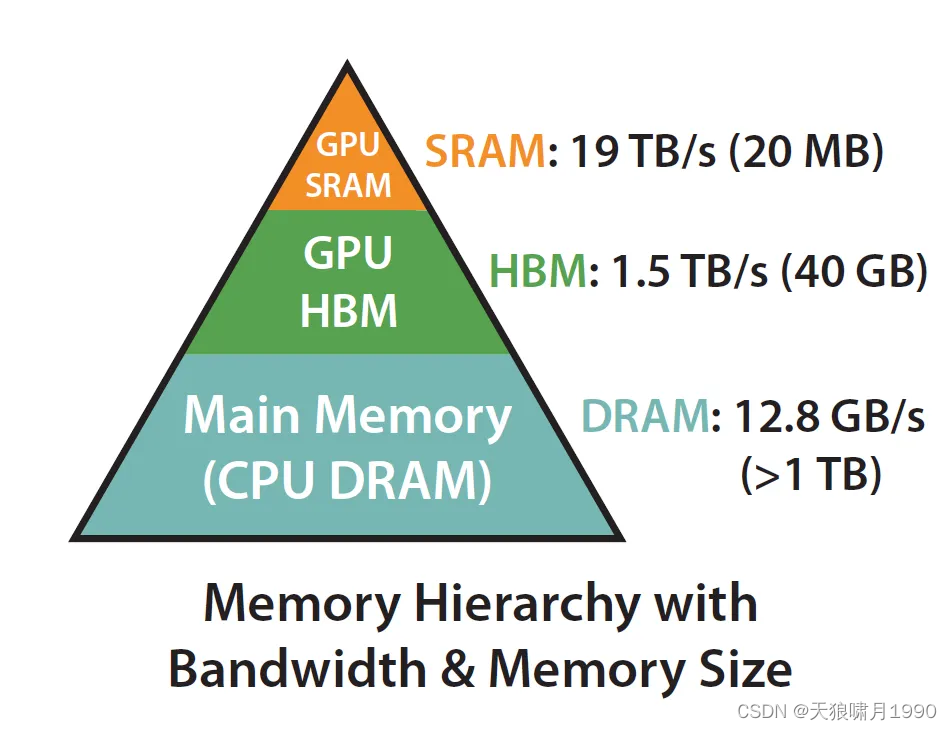
扩展：在计算机体系结构里，内存不是单一的构建，内存存储都是分层的。一般规则是：Memory IO speed 内存速度越快，成本越高，容量越小。

GPU SRAM，19TB/s (20 MB)，Static RAM, 静态随机存储器
GPU HBM，1.5TB/s (40 GB)，high Boardwidth memory, 高带宽内存
GPU DRAM，12.8GB/s (>1 TB)，main memory

实际上，要充分利用内存、实现IO-aware，关键在于充分利用静态随机存取存储器 (SPAM)比高带宽内存 (HBM)快得多的事实，确保减少两者之间的通信。

（HBM，这是导致CUDA内存溢出的因素之一)

Flash Attention

Flash Attention 采样分而治之的思想，将大矩阵切块加载到SRAM中，计算每个分块的m和l值。利用上一轮m和l值结合新的子块迭代计算，最终计算出整个矩阵的树枝。Flash Attention基本上可以归结为两个主要思想：

Tiling (在前向和后向传递中使用) - 简单讲就是将NxN的softmax分数矩阵划分为块。
重新计算(因为每个块的系数不一样，Flash Attention每融合一个小块，就需要调整一下之前块的系数，去保持一致！)
传统attention需要分配完整的NxN矩阵(S, P)，这是main需要解决的瓶颈，这也是Flash Attention主要解决的问题，将复杂度从 $O(N^2)$ 降低到 $O(N)$ 。

整个过程不用存储中间变量S和P矩阵，节省了效率。因为Attention 操作最大的问题就是每次操作都要从HBM把数据加载到GPU SRAM，运算结束后又从SRAM复制到HBM。这类似于cpu的寄存器与内存的关系，因此最容易的优化方法就是避免这种数据的来回移动，即编译器行话"kernel fusion"。

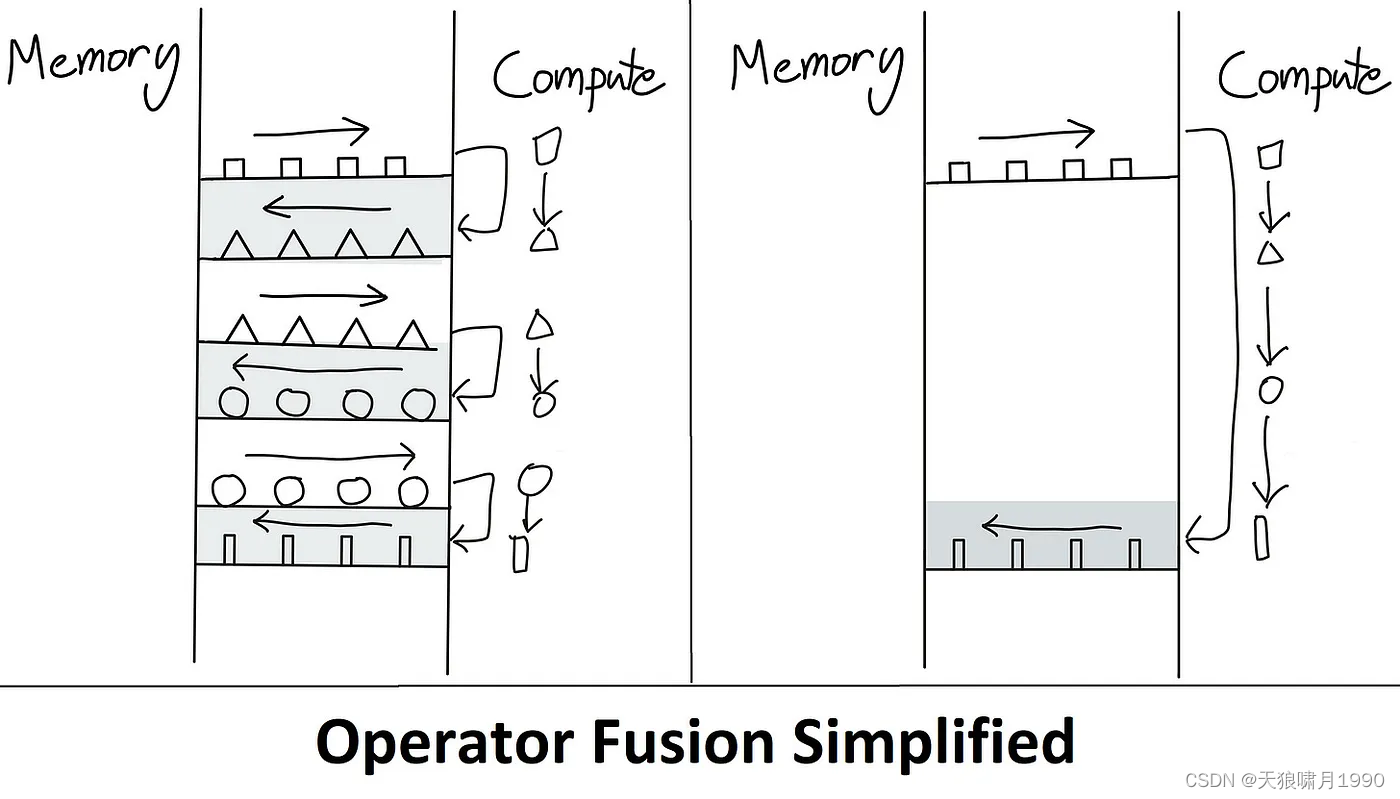
Flash Attention Algorithm

假设输入一个一维向量 $x^{(i)} = [x_1,x_2,...,x_B]$ ，对应于QK=Sij相似度矩阵中的一行向量。

1. softmax分块计算：

m(x) = max(xi)，这是rowmax 操作。这是单个值。
$f(x) = [e^{x_1-m(x),..., e^{x_B-m(x)}}]$ 。对应原公式的 $\tilde{P}_{ij}$ ，then why xi-m(x)?这是为了数值稳定，每个数减去相同的任一常量，其softmax值不变。==》减去最大的元素，保证最大值为 $e^0=1$ ，因为在0～1之间时，浮点数的精度是最大的。
$l(x) = \sum_if(x)_i$ ，对应原公式 $\tilde{l}_{ij}$ ，这是rowsum 操作。
$so\!ftmax = \frac{f(x)}{l(x)}$ , softmax除法可以写成 $diag(l(x))^{-1}$ ，把l(x)拉伸成diag的主要原因是把更新公式写成矩阵乘法的形式。

2. Flash Attention每次都是合并两块：previous blocks result + latest block。如何保证每一个小块的合并结果与原有attention结果相同？搞好softmax系数的一致性！

因为each step都需要重新计算 $m(x) = max(m^{(i)})$ ，而m(x)是变的，前面blocks在合并之前，需要先通过 $m_i - m_i^{new}$ 来修正之前block的系数， $\tilde{m}_{ij}$ 是指第ij单个block的max(x)，不涉及之前blocks的max值。
$m(x) = m([x^{(1), x^{(2)}}]) = max(m(x^{(1)}, m^{(2)}))$
$f(x) = [e^{m(x^{(1)})-m(x))}f(x^{(1)}, e^{m(x^{(2)})-m(x))}f(x^{(2)})]$
$l(x) = e^{m(x^{(1)})-m(x))}l(x^{(1)}, e^{m(x^{(2)})-m(x))}l(x^{(2)})$ ，修正系数 $m_i - m_i^{new}$ 保持一致，因为这两个blocks的softmax系数不一致， $m(x^{(2)})-m(x)$ 保证最新的single block的softmax系数与之前的一致！
$so\!ftmax = \frac{f(x)}{l(x)}$

举例：假设 $x \in R^6$ ，并且它被分成3块： $x^{(1)} = [1,3]$ , $x^{(2)} = [2,4]$ , $x^{(3)} = [3,2]$

我们先计算前两块：

$m(x^{(1)})=3, f(x^{(1)})=[e^{-2},1], l(x^{(1)})=(e^{-2}+1)$
$m(x^{(2)})=4, f(x^{(2)})=[e^{-2},1], l(x^{(2)})=(e^{-2}+1)$

我们根据上面的结果计算前两块的结果：

$m(x) = max(m(x^{(1)}), m(x^{(2)})) = max(3,4)=4$
$f(x) = [e^{3-4}f(x^{(1)}), e^{4-4}f(x^{(2)})]$
$l(x) = e^{3-4}l(x^{(1)}) + e^{4-4}l(x^{(2)})$

为什么上面的结果是正确的呢？首先m(x)应该非常明显，4个数中的最大数肯定就是分成两组后的最大中的较大者。而f(x)计算的核心就是在𝑓(𝑥(1))𝑓(𝑥(1))前乘以𝑒3−4𝑒3−4以及在𝑓(𝑥(2))𝑓(𝑥(2))前乘以𝑒4−4𝑒4−4。l(x)的计算和f(x)是类似的。为什么需要在𝑓(𝑥(1))𝑓(𝑥(1))前乘以𝑒3−4𝑒3−4？因为在计算𝑓(𝑥(1))𝑓(𝑥(1))时最大的数是3，因此前两个数的指数都乘以了𝑒−3𝑒−3。但是现在前4个数的最大是4了，后面两个数的指数乘以了𝑒−4𝑒−4，因此直接合并为[𝑓(𝑥(1)),𝑓(𝑥(2))][𝑓(𝑥(1)),𝑓(𝑥(2))]是不对的，需要把前面两个数再乘以𝑒3−4=𝑒−1𝑒3−4=𝑒−1。而后面两个数本来就乘以了𝑒−4𝑒−4，所以不用变

计算output Oi：我们把一个很大的x拆分成长度为B的blocks，用上面的算法计算block 1和block 2，然后合并其结果；接着计算第3块，并将above 结果与第三块合并; ... =》所以，我们在定义时，可以把空块x=[], m(x)=-inf, f(x)=[], l(x)=0，这样我们就可以把第一块block的计算转换成block 1和空块的合并，使得循环可以从第一块开始！

$O_1 = diag(l_1)^{-1}(0 * 0 + e^{\tilde{m}_{ij}-m_i^{new}}\tilde{P}_{ij}V_j)$
$O_2 = diag(l_i^{new})^{-1}(diag(l_i)O_ie^{m_i-m_i^{new}} + e^{\tilde{m}_{ij}-m_i^{new}}\tilde{P}_{ij}V_j)$

因为Flash Attention不存储中间变量S和P矩阵，所以我们用 $diag(l_i)O_i$ 反推出之前的PV值，再用 $e^{m_i-m_i^{new}}$ 修正系数，最后加上第ij块 $e^{\tilde{m}_{ij}-m_i^{new}}\tilde{P}_{ij}V_j)$ with single $e^{\tilde{m}_{ij}}$ ，得到的结果最后再除以 $diag(l_i^{new})^{-1}$ 保持softmax运算完整性。