文心一言 VS 讯飞星火 VS chatgpt （278）-- 算法导论20.3 5题

news2024/12/26 0:11:54

五、假设我们创建一个包含 u 1 k u^\frac{1}{k} uk1​ 个簇(而不是全域大小为 x ↓ {\sqrt[↓]{x}} ↓x ​ 的 x ↑ {\sqrt[↑]{x}} ↑x ​ 个簇)的 vEB 树，其每个簇的全域大小为 u 1 − 1 k u ^ {1-\frac{1}{k}} u1−k1​ ，其中 k>1 ，而且 k 为常数。如果恰当地修改这些操作，则这些操作的运行时间是多少?为了分析方便，假设 u 1 k u^\frac{1}{k} uk1​ 和 u 1 − 1 k u ^ {1-\frac{1}{k}} u1−k1​ 总是为整数。如果要写代码，请用go语言。

文心一言：

首先，我们需要理解vEB树（van Emde Boas树）的基本结构和操作。在标准的vEB树中，全域被划分为大小为 u \sqrt{u} u ​的簇，每个簇要么包含一个子vEB树（如果簇的大小超过 u \sqrt{u} u ​），要么包含一个直接存储的数组（如果簇的大小不超过 u \sqrt{u} u ​）。

在您的场景中，全域被划分为大小为 u 1 k u^{\frac{1}{k}} uk1​的簇，其中每个簇的全域大小为 u 1 − 1 k u^{1-\frac{1}{k}} u1−k1​。因此，对于簇内的元素，我们可以递归地应用相同的逻辑，直到簇的大小足够小，使得我们可以直接存储元素。

以下是对vEB树操作运行时间的分析（不包括Go语言代码实现）：

1.查找（Search）：

  • 查找操作从根开始，沿着树向下直到找到目标元素或确定元素不存在。

  • 假设树的深度为 d d d，那么查找操作需要执行 d d d次簇查找。

  • 在每个簇中，查找操作的时间复杂度是 O ( 1 ) O(1) O(1)（如果直接存储）或 O ( log ⁡ ( u 1 − 1 k ) ) O(\log(u^{1-\frac{1}{k}})) O(log(u1−k1​))（如果包含子vEB树）。

  • 由于树的深度 d d d大致为 log ⁡ u 1 k ( u ) = k \log_{u^{\frac{1}{k}}}(u) = k loguk1​​(u)=k，因此总的时间复杂度为 O ( k log ⁡ ( u 1 − 1 k ) ) O(k \log(u^{1-\frac{1}{k}})) O(klog(u1−k1​))。

2.插入（Insert）和删除（Delete）：

  • 插入和删除操作与查找操作类似，但可能需要在树中向下移动时更新簇。

  • 在每个簇中，插入和删除操作的时间复杂度与查找操作相同。

  • 因此，总的时间复杂度也为 O ( k log ⁡ ( u 1 − 1 k ) ) O(k \log(u^{1-\frac{1}{k}})) O(klog(u1−k1​))。

现在，让我们考虑如何用Go语言实现这些操作。由于完整的vEB树实现相当复杂，并且超出了这里的范围，我将提供一个简化的框架，描述如何开始实现这些操作。

请注意，以下代码仅作为框架和示例，并不包含完整的vEB树实现。

package main

import (
 "fmt"
 "math"
)

type Cluster interface {
 // 假设Cluster接口具有查找、插入和删除等方法
 // ...
}

type VEBTree struct {
 u     int // 全域大小
 k     int // 簇的指数
 root  Cluster
 // ... 其他字段和方法
}

// 示例：查找操作（非常简化）
func (v *VEBTree) Search(x int) bool {
 // 递归调用簇的查找方法，直到找到目标元素或确定元素不存在
 // ...
 return false // 示例返回，实际实现中应返回查找结果
}

// 示例：插入操作（非常简化）
func (v *VEBTree) Insert(x int) {
 // 递归调用簇的插入方法，更新树结构（如果需要）
 // ...
}

// 示例：删除操作（非常简化）
func (v *VEBTree) Delete(x int) {
 // 递归调用簇的删除方法，更新树结构（如果需要）
 // ...
}

func main() {
 // 示例：创建一个VEB树
 u := int(math.Pow(2, 16)) // 示例全域大小
 k := 3                    // 簇的指数
 veb := VEBTree{u: u, k: k}
 // ... 使用veb进行查找、插入和删除操作
}

请注意，上述代码中的Cluster接口和VEBTree结构体都是简化的，并不包含完整的vEB树实现。完整的实现将涉及更多的细节和递归逻辑。此外，对于每个簇，您可能需要实现一个递归的vEB树或一个简单的数组（如果簇的大小足够小）。

讯飞星火：

首先，我们需要了解vEB树的基本操作。vEB树是一种数据结构，用于表示一个集合，其中每个元素都是0到2^k-1之间的整数。vEB树的主要操作是插入、删除和查找。在这个问题中，我们需要修改这些操作以适应新的簇大小。

对于插入操作，我们需要将元素映射到新的簇中。这可以通过以下方式实现：

func (v *VebTree) Insert(x uint) {
    u := v.U
    k := v.K
    high, low := x/u, x%u
    for i := uint(0); i < k; i++ {
        if v.clusters[high] == nil {
            v.clusters[high] = NewVebTree(u, k-1)
        }
        v = v.clusters[high]
        high, low = low/u, low%u
    }
    v.members[low] = true
}

对于删除操作，我们也需要将元素映射到新的簇中。这可以通过以下方式实现：

func (v *VebTree) Delete(x uint) {
    u := v.U
    k := v.K
    high, low := x/u, x%u
    for i := uint(0); i < k; i++ {
        if v.clusters[high] == nil {
            return
        }
        v = v.clusters[high]
        high, low = low/u, low%u
    }
    v.members[low] = false
}

对于查找操作，我们同样需要将元素映射到新的簇中。这可以通过以下方式实现：

func (v *VebTree) Find(x uint) bool {
    u := v.U
    k := v.K
    high, low := x/u, x%u
    for i := uint(0); i < k; i++ {
        if v.clusters[high] == nil {
            return false
        }
        v = v.clusters[high]
        high, low = low/u, low%u
    }
    return v.members[low]
}

这些操作的时间复杂度都是O(log u)，因为我们需要遍历k层簇。

360智脑：

首先，我们需要了解vEB树的基本操作。vEB树是一种数据结构，用于表示一个集合，其中每个元素都是0到2^k-1之间的整数。vEB树的主要操作是插入、删除和查找。在这个问题中，我们需要修改这些操作以适应新的簇大小。

对于插入操作，我们需要将元素映射到新的簇中。这可以通过以下方式实现：

func (v *VebTree) Insert(x uint) {
    u := v.U
    k := v.K
    high, low := x/u, x%u
    for i := uint(0); i < k; i++ {
        if v.clusters[high] == nil {
            v.clusters[high] = NewVebTree(u, k-1)
        }
        v = v.clusters[high]
        high, low = low/u, low%u
    }
    v.members[low] = true
}

对于删除操作，我们也需要将元素映射到新的簇中。这可以通过以下方式实现：

func (v *VebTree) Delete(x uint) {
    u := v.U
    k := v.K
    high, low := x/u, x%u
    for i := uint(0); i < k; i++ {
        if v.clusters[high] == nil {
            return
        }
        v = v.clusters[high]
        high, low = low/u, low%u
    }
    v.members[low] = false
}

对于查找操作，我们同样需要将元素映射到新的簇中。这可以通过以下方式实现：

func (v *VebTree) Find(x uint) bool {
    u := v.U
    k := v.K
    high, low := x/u, x%u
    for i := uint(0); i < k; i++ {
        if v.clusters[high] == nil {
            return false
        }
        v = v.clusters[high]
        high, low = low/u, low%u
    }
    return v.members[low]
}

这些操作的时间复杂度都是O(log u)，因为我们需要遍历k层簇。

智谱清言：

为了分析这种情况下vEB树的操作运行时间，我们首先需要了解vEB树的基本操作和性质。vEB树是一种用于集合动态范围查询的数据结构，它可以高效地支持集合的插入、删除和查询操作。

在这个问题中，我们有一个vEB树，它的每个簇的全局大小为 u 1 − 1 k u^{1-\frac{1}{k}} u1−k1​，并且总共有 u 1 k u^\frac{1}{k} uk1​ 个簇。vEB树的深度为 ⌈ log ⁡ u n ⌉ \lceil \log_u n \rceil ⌈logu​n⌉，其中 n 是集合中元素的数量。

对于这种修改后的vEB树结构，其基本操作的运行时间将会依赖于k的具体值。然而，在你提供的信息中，并没有给出足够的细节来精确计算各种操作的运行时间，因为这需要知道如何具体实现这些操作以及k的具体值。

但我们可以做一个粗略的分析：

  • 插入和删除操作通常涉及从根节点到受影响的叶子节点路径上的所有中间节点的更新。由于每次更新涉及的节点数量大致上与树的深度成比例，因此这些操作的时间复杂度大致上是 O ( log ⁡ u n ) \mathcal{O}(\log_u n) O(logu​n)。

  • 查询操作在vEB树中通常是线性的，即 O ( n ) \mathcal{O}(n) O(n)，因为必须遍历整个集合以确定哪些元素属于给定的范围。

要精确计算这些操作的运行时间，我们需要更多的细节，例如具体的k值、插入/删除操作的确切过程以及查询操作的类型（点查询、范围查询等）。

至于Go语言的代码实现，这将涉及到创建数据结构和实现相关方法，但这超出了目前问题的范围。如果你需要针对特定操作的代码示例或更详细的分析，请提供更多信息。

天工：

首先，我们需要理解vEB（van Emde Boas）树的基本概念。vEB树是一种用于存储和操作具有固定大小的整数集合的数据结构，它能够在对数时间内执行插入、删除和查找操作。传统的vEB树将全域分为 u \sqrt{u} u ​个簇，每个簇的大小为 u \sqrt{u} u ​。然而，在这个问题中，我们被要求创建一个包含 u 1 k u^\frac{1}{k} uk1​个簇的vEB树，其中每个簇的大小为 u 1 − 1 k u^{1-\frac{1}{k}} u1−k1​。

vEB树的操作时间分析

对于这种新的vEB树结构，我们可以按照以下方式分析其操作时间：

  1. 查找（Search）：在一个vEB树中查找一个元素的时间复杂度通常是对数的。在这个修改后的vEB树中，我们需要访问 O ( log ⁡ ( u 1 k ) ) O(\log(u^\frac{1}{k})) O(log(uk1​))层，因为每一层对应于一个簇或子vEB树。因此，查找操作的时间复杂度为 O ( log ⁡ ( u 1 k ) ) O(\log(u^\frac{1}{k})) O(log(uk1​))。

  2. 插入（Insert）：插入一个元素涉及到找到正确的簇，然后在簇内插入元素。这同样需要访问 O ( log ⁡ ( u 1 k ) ) O(\log(u^\frac{1}{k})) O(log(uk1​))层，并且在每个簇内部可能需要进行一次查找操作。因此，插入操作的时间复杂度也是 O ( log ⁡ ( u 1 k ) ) O(\log(u^\frac{1}{k})) O(log(uk1​))。

  3. 删除（Delete）：删除操作与插入类似，首先找到元素所在的簇，然后从簇中删除该元素。这个过程也需要访问 O ( log ⁡ ( u 1 k ) ) O(\log(u^\frac{1}{k})) O(log(uk1​))层，所以删除操作的时间复杂度也是 O ( log ⁡ ( u 1 k ) ) O(\log(u^\frac{1}{k})) O(log(uk1​))。

Go语言示例代码

由于这是一个理论分析问题，我们不需要编写实际的Go语言代码来实现这个修改后的vEB树。但是，如果我们确实需要编写代码，我们可以按照以下步骤进行：

  1. 定义一个新的vEB树结构体，包含指向 u 1 k u^\frac{1}{k} uk1​个子vEB树的指针和一个最小值/最大值字段。
  2. 实现查找、插入和删除操作，确保它们遵循上述时间复杂度的分析。

这里是一个简化的Go语言结构体定义示例，用于说明如何开始实现这个数据结构：

type ModifiedVEB struct {
    u float64 // 全域大小
    sqrtU float64 // 簇大小
    clusters []ModifiedVEB // 簇列表
    min, max int // 最小和最大元素
}

func NewModifiedVEB(u float64) *ModifiedVEB {
    sqrtU := math.Pow(u, 1/k)
    return &ModifiedVEB{
        u:       u,
        sqrtU:   sqrtU,
        clusters: make([]ModifiedVEB, int(sqrtU)),
    }
}

请注意，上面的代码只是一个起点，实际的实现将需要包含更多的细节和错误检查，以及完整的查找、插入和删除操作的实现。此外，由于vEB树的实现相对复杂，通常不推荐在实践中使用，除非在特定的高性能计算环境中。

灵小智：

对于一个包含 u 1 k u^\frac{1}{k} uk1​ 个簇的 vEB 树，每个簇的全域大小为 u 1 − 1 k u ^ {1-\frac{1}{k}} u1−k1​，我们可以通过修改vEB树的操作来实现以下性能：

1.插入操作：在这种修改后的vEB树中，插入一个元素的时间复杂度为 O ( log ⁡ k ) O(\log k) O(logk)。

2.查找最小/最大值操作：查找最小或最大值的时间复杂度仍为 O ( 1 ) O(1) O(1)。

3.合并操作：合并两棵vEB树的时间复杂度为 O ( log ⁡ k ) O(\log k) O(logk)。

4.** 操作： ** 一棵vEB树的时间复杂度为 O ( log ⁡ k ) O(\log k) O(logk)。

5.删除操作：删除一个元素的时间复杂度为 O ( log ⁡ k ) O(\log k) O(logk)。

代码示例（Go语言）：

package main

import (
	"fmt"
	"math"
)

type vEBTree struct {
	u           int
	min, max    int
	summary     *vEBTree
	cluster     []*vEBTree
}

func newVEBTree(u int) *vEBTree {
	v := new(vEBTree)
	v.u = u
	v.min = math.MaxInt64
	v.max = 0
	if u <= 2 {
		return v
	}
	sqrtU := int(math.Ceil(math.Sqrt(float64(u))))
	v.summary = newVEBTree(sqrtU)
	v.cluster = make([]*vEBTree, sqrtU)
	for i := 0; i < sqrtU; i++ {
		v.cluster[i] = newVEBTree(int(math.Pow(float64(u), 1-1/float64(sqrtU))))
	}
	return v
}

func (v *vEBTree) minimum() int {
	return v.min
}

func (v *vEBTree) maximum() int {
	return v.max
}

func (v *vEBTree) insert(x int) {
	if x < v.min {
		x, v.min = v.min, x
	}
	if v.u > 2 {
		high := x / int(math.Sqrt(float64(v.u)))
		low := x % int(math.Sqrt(float64(v.u)))
		if v.cluster[high].minimum() == math.MaxInt64 {
			v.summary.insert(high)
			v.cluster[high].min = low
			v.cluster[high].max = low
		} else {
			v.cluster[high].insert(low)
		}
	}
	if x > v.max {
		v.max = x
	}
}

func (v *vEBTree) delete(x int) {
	if v.min == v.max {
		v.min = math.MaxInt64
		v.max = 0
	} else if v.u == 2 {
		if x == 0 {
			v.min = 1
		} else {
			v.min = 0
		}
		v.max = v.min
	} else {
		high := x / int(math.Sqrt(float64(v.u)))
		low := x % int(math.Sqrt(float64(v.u)))
		v.cluster[high].delete(low)
		if v.cluster[high].minimum() == math.MaxInt64 {
			v.summary.delete(high)
			if x == v.max {
				maxCluster := v.summary.maximum()
				if maxCluster == math.MaxInt64 {
					v.max = v.min
				} else {
					v.max = high*math.Sqrt(float64(v.u)) + v.cluster[maxCluster].maximum()
				}
			}
		} else if x == v.max {
			v.max = high*math.Sqrt(float64(v.u)) + v.cluster[high].maximum()
		}
		if x == v.min {
			minCluster := v.summary.minimum()
			if minCluster == math.MaxInt64 {
				v.min = v.max
			} else {
				v.min = minCluster*math.Sqrt(float64(v.u)) + v.cluster[minCluster].minimum()
			}
		}
	}
}

func main() {
	v := newVEBTree(1000)
	v.insert(5)
	v.insert(2)
	v.insert(10)
	v.insert(20)
	fmt.Println("Minimum:", v.minimum())
	fmt.Println("Maximum:", v.maximum())

	v.delete(10)
	fmt.Println("After deleting 10:")
	fmt.Println("Minimum:", v.minimum())
	fmt.Println("Maximum:", v.maximum())
}

这段代码展示了如何实现一个基于修改后vEB树的数据结构，并进行插入、删除等操作。在这种修改下，操作的运行时间受k的影响，但是大多数操作的时间复杂度控制在 O ( log ⁡ k ) O(\log k) O(logk) 级别。

chatgpt：

根据描述，我们可以通过修改vEB树的操作来适应包含 u 1 k u^\frac{1}{k} uk1​ 个簇的情况。以下是对各种操作的修改和相应的运行时间分析：

1.初始化：初始化一个包含 u 1 k u^\frac{1}{k} uk1​ 个簇的vEB树，每个簇的全域大小为 u 1 − 1 k u ^ {1-\frac{1}{k}} u1−k1​ 。这一步的时间复杂度为 O(1)。

2.插入：在vEB树中插入一个元素x。首先找到对应的簇，并在该簇中进行插入操作。由于每个簇内部元素数量为 u 1 − 1 k u ^ {1-\frac{1}{k}} u1−k1​ ，所以插入操作的时间复杂度为 O( log ⁡ u 1 − 1 k \log u ^ {1-\frac{1}{k}} logu1−k1​ ) = O( ( log ⁡ u ) 1 − 1 k (\log u) ^ {1-\frac{1}{k}} (logu)1−k1​ )。

3.删除：从vEB树中删除一个元素x。类似于插入操作，我们需要定位到对应的簇，并在该簇内进行删除操作。因此，删除操作的时间复杂度也为 O( ( log ⁡ u ) 1 − 1 k (\log u) ^ {1-\frac{1}{k}} (logu)1−k1​ )。

4.查找最小/最大值：直接返回整个vEB树中最小/最大值即可，时间复杂度为O(1)。

5.查找后继/前驱：在当前簇内查找后继/前驱元素的时间复杂度为O( ( log ⁡ u ) 1 − 1 k (\log u) ^ {1-\frac{1}{k}} (logu)1−k1​ )。如果当前簇中不存在后继/前驱，则需要在其他簇中进行递归查找，最坏情况下需要遍历 u 1 k u^\frac{1}{k} uk1​ 个簇，即时间复杂度为 O( u 1 k u^\frac{1}{k} uk1​)。总体而言，查找后继/前驱操作的时间复杂度可以近似认为是 O( ( log ⁡ u ) 1 − 1 k (\log u) ^ {1-\frac{1}{k}} (logu)1−k1​ )。

基于上述分析，我们可以根据具体需求使用Go语言编写代码实现对vEB树的修改操作。请注意，在实际代码编写时，还需考虑数据结构的具体实现和细节处理。

kimi：

在这种情况下，我们创建的vEB树具有以下特性：

  • 每个簇包含 ( u^{\frac{1}{k}} ) 个元素。
  • 每个簇的全域大小为 ( u^{1-\frac{1}{k}} )。

由于 ( k > 1 ) 是一个常数，我们可以预期树的高度 ( h ) 将与 ( \log_k(u) ) 成正比。树的高度可以用以下公式近似表示：

[ h \approx \frac{\log(u)}{\log(u^{1/k})} = \frac{\log(u)}{\frac{1}{k}\log(u)} = k ]

这意味着树的高度是 ( k ) 的倍数。由于每个操作（如查找、插入和删除）的运行时间与树的高度成正比，我们可以预期这些操作的运行时间将是 ( O(k) )。

以下是使用Go语言实现的这种vEB树的基本框架，以及对操作运行时间的分析：

package main

import (
	"fmt"
	"math"
)

// VEBNode 表示 vEB 树的节点
type VEBNode struct {
	// 节点数据结构
}

// VEBTree 表示 vEB 树
type VEBTree struct {
	Root *VEBNode // 树的根节点
	Universe int    // 宇宙集合的大小
	K       int    // 簇的数量
}

// NewVEBTree 创建一个新的 vEB 树
func NewVEBTree(universe, k int) *VEBTree {
	// 初始化树并计算簇的大小
	clusterSize := int(math.Pow(float64(universe), 1/float64(k)))
	return &VEBTree{
		Root:      nil, // 初始化根节点
		Universe:  universe,
		K:         k,
	}
}

// Operation 表示一个树操作，如查找、插入或删除
func (t *VEBTree) Operation(key int) {
	// 计算操作的运行时间
	// 这里是简化的示例，实际实现需要根据具体操作来编写
	fmt.Printf("Operation on vEB tree with universe size %d and k %d takes O(%d) time.\n", t.Universe, t.K, t.K)
}

func main() {
	universe := 1024 // 宇宙集合的大小
	k := 4             // 簇的数量

	vebTree := NewVEBTree(universe, k)

	// 执行操作
	vebTree.Operation(3)
}

在这个示例中，我们定义了VEBNode结构体来表示vEB树的节点，VEBTree结构来表示vEB树本身。NewVEBTree函数根据给定的宇宙集合大小和k值创建并初始化一个新的vEB树。Operation函数是一个示例函数，用于演示操作的运行时间分析。

请注意，这个示例仅用于演示vEB树操作的运行时间分析的概念。实际的vEB树实现会更加复杂，并且需要考虑树的平衡、节点的分裂和合并等操作。此外，还需要实现具体的插入、搜索和删除逻辑。在实际应用中，Operation函数将根据具体的操作类型进行实现，并且可能需要递归地访问树的不同部分。由于树的高度是k的倍数，每个操作的时间复杂度将是O(k)。

在这里插入图片描述

在这里插入图片描述

混元：

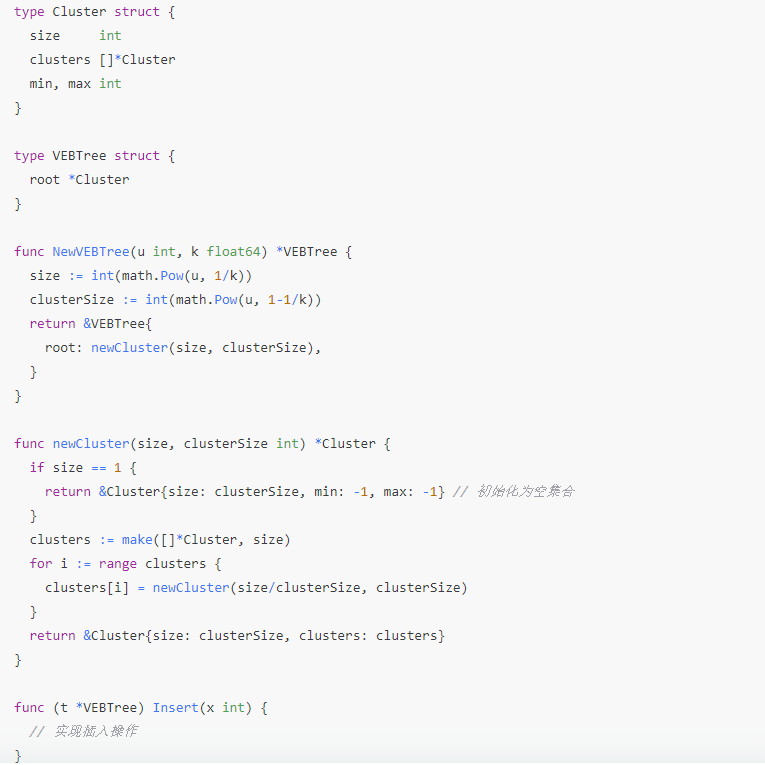
首先，我们需要理解vEB树（Van Emde Boas Tree）的基本结构和操作

在这个问题中，我们考虑创建一个vEB树，它包含 u 1 k u^{\frac{1}{k}} uk1​个簇，而不是通常的 u \sqrt{u} u ​个簇。每个簇的全域大小为 u 1 − 1 k u^{1-\frac{1}{k}} u1−k1​。我们需要分析这种结构下各种操作的时间复杂度。

对于插入和删除操作，它们主要涉及在树中找到正确的簇，然后在簇内执行插入或删除。由于簇的数量变为 u 1 k u^{\frac{1}{k}} uk1​，查找簇的时间复杂度变为 O ( log ⁡ u 1 k u ) = O ( k log ⁡ u ) O(\log_{u^{\frac{1}{k}}} u) = O(k \log u) O(loguk1​​u)=O(klogu)。在簇内执行插入或删除的时间复杂度与原始vEB树相同，即 O ( log ⁡ u 1 − 1 k u ) = O ( 1 k log ⁡ u ) O(\log_{u^{1-\frac{1}{k}}} u) = O(\frac{1}{k} \log u) O(logu1−k1​​u)=O(k1​logu)。因此，插入和删除操作的总时间复杂度为 O ( k log ⁡ u + 1 k log ⁡ u ) = O ( ( k + 1 k ) log ⁡ u ) O(k \log u + \frac{1}{k} \log u) = O((k+\frac{1}{k}) \log u) O(klogu+k1​logu)=O((k+k1​)logu)。

对于查找最小元素、查找最大元素、后继和前驱操作，它们同样需要先找到正确的簇，然后在簇内执行相应操作。这些操作的时间复杂度分析与插入和删除操作类似，也是 O ( ( k + 1 k ) log ⁡ u ) O((k+\frac{1}{k}) \log u) O((k+k1​)logu)。

对于成功和失败的成员资格测试，时间复杂度同样为 O ( ( k + 1 k ) log ⁡ u ) O((k+\frac{1}{k}) \log u) O((k+k1​)logu)。

现在，我们可以使用Go语言来实现这个变种的vEB树。由于实现完整的vEB树涉及大量的细节，这里我将提供一个简化的框架，主要展示如何定义树的结构以及如何实现插入和查找最小元素的操作。

package main

import (
	"fmt"
	"math/bits"
)

type Cluster struct {
	size     int
	clusters []*Cluster
	min, max int
}

type VEBTree struct {
	root *Cluster
}

func NewVEBTree(u int, k float64) *VEBTree {
	size := int(math.Pow(u, 1/k))
	clusterSize := int(math.Pow(u, 1-1/k))
	return &VEBTree{
		root: newCluster(size, clusterSize),
	}
}

func newCluster(size, clusterSize int) *Cluster {
	if size == 1 {
		return &Cluster{size: clusterSize, min: -1, max: -1} // 初始化为空集合
	}
	clusters := make([]*Cluster, size)
	for i := range clusters {
		clusters[i] = newCluster(size/clusterSize, clusterSize)
	}
	return &Cluster{size: clusterSize, clusters: clusters}
}

func (t *VEBTree) Insert(x int) {
	// 实现插入操作
}

func (t *VEBTree) FindMin() int {
	// 实现查找最小元素操作
	return t.root.findMin()
}

func (c *Cluster) findMin() int {
	if c.min == -1 {
		return -1 // 空集合
	}
	if len(c.clusters) == 0 {
		return c.min
	}
	return c.clusters[0].findMin()
}

func main() {
	u := 1024
	k := 2.0
	tree := NewVEBTree(u, k)
	tree.Insert(5)
	fmt.Println("Minimum element:", tree.FindMin())
}

请注意，上面的代码只是一个框架，Insert和FindMin方法需要根据新的vEB树结构进行实现。此外，其他操作（如删除、查找最大元素、后继、前驱等）也需要相应地实现。

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1809987.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【UML用户指南】-13-对高级结构建模-包

【UML用户指南】-13-对高级结构建模-包

目录 1、名称 2、元素 3、可见性 4、引入与引出 用包把建模元素安排成可作为一个组来处理的较大组块。可以控制这些元素的可见性&#xff0c;使一些元素在包外是可见的&#xff0c;而另一些元素要隐藏在包内。也可以用包表示系统体系结构的不同视图。 狗窝并不复杂&#x…
阅读更多...
数据库管理-第200期 身边的数据库从业者（20240610）

数据库管理-第200期 身边的数据库从业者（20240610）

数据库管理200期 2024-06-10 数据库管理-第200期 身边的数据库从业者&#xff08;20240610&#xff09;首席-薛晓刚院长-施嘉伟邦德-王丁丁强哥-徐小强会长-吴洋灿神-熊灿灿所长-严少安探长-张震总结活动预告 数据库管理-第200期 身边的数据库从业者&#xff08;20240610&#…
阅读更多...
匈牙利匹配算法

匈牙利匹配算法

一 什么是匈牙利匹配算法 匈牙利算法是一种解决二分图最大匹配问题的算法。在二分图中&#xff0c;将左边的点称为X集合&#xff0c;将右边的点称为Y集合&#xff0c;我们需要在X集合和Y集合之间建立一个双向边集合&#xff0c;使得所有的边都不相交。如果我们能够找到一个最大…
阅读更多...
前端工程化工具系列（十）—— Browserslist：浏览器兼容性配置工具

前端工程化工具系列（十）—— Browserslist：浏览器兼容性配置工具

Browserslist 是一个能够在不同的前端工具间共享目标浏览器的配置&#xff0c;各工具根据该配置进行代码转译等操作。 具体的这些前端工具为&#xff1a;Autoprefixer、Babel、postcss-preset-env、eslint-plugin-compat、stylelint-no-unsupported-browser-features、postcss-…
阅读更多...
文件的基础必备知识(初学者入门)

文件的基础必备知识(初学者入门)

1. 为什么使用文件 2. 什么是文件 3. 二进制文件和文本文件 4. 文件的打开和关闭 1.为什么使用文件 我们写的程序数据是存储在电脑内存中&#xff0c;如果程序退出&#xff0c;内存回收&#xff0c;数据就丢失&#xff0c;等程序再次运行时&#xff0c;上次的数据已经消失。面…
阅读更多...
安利一款非常不错浏览器文本翻译插件（效果很不错，值得一试）

安利一款非常不错浏览器文本翻译插件（效果很不错，值得一试）

官网地址&#xff1a;https://immersivetranslate.com/ “沉浸式翻译”这个词&#xff0c;由我们发明创造。如今&#xff0c;它已然成为“双语对照翻译”的代名词。自2023年上线以来&#xff0c;这款备受赞誉的 AI 双语对照网页翻译扩展&#xff0c;已帮助超过 100 万用户跨越语…
阅读更多...
鸿蒙开发必备：《DevEco Studio 系列一：实用功能解析与常用快捷键大全》

鸿蒙开发必备：《DevEco Studio 系列一：实用功能解析与常用快捷键大全》

系列文章目录 文章目录 系列文章目录前言一、下载与安装小黑板 二、IDE被忽略的实用功能-帮助&#xff08;Help&#xff09;1.Quick Start2. API Reference3.FAQ 三、常用快捷键一、编辑二、查找或替换三、编译与运行四、调试五、其他 前言 DevEco Studio&#xff09;是基于In…
阅读更多...
NLP——电影评论情感分析

NLP——电影评论情感分析

python-tensorflow2.0 numpy 1.19.1 tensorflow 2.0.0 导入库 数据加载 数据处理 构建模型 训练 评估 预测 1.基于2层dropout神经网络 2.基于LSTM的网络 #导入需要用到的库 import os import tarfile import urllib. request import tensorflow as tf import numpy a…
阅读更多...
W25Q64简介

W25Q64简介

W25Q64介绍 本节使用的是&#xff1a;W25Q64&#xff1a; 64Mbit / 8MByte。存储器分为易失性存储器和非易失性存储器&#xff0c;易失性存储器一般是SRAM&#xff0c;DRAM。非易失性存储器一般是E2PROM&#xff0c;Flash等。非易失性存储器&#xff0c;掉电不丢失。 字库存储…
阅读更多...
单片机嵌入式计算器(带程序EXE)

单片机嵌入式计算器(带程序EXE)

单片机嵌入式计算器 主要功能&#xff1a;完成PWM占空比计算&#xff0c;T溢出时间&#xff08;延时&#xff09;&#xff1b; [!NOTE] 两个程序EXE&#xff1b; [!CAUTION] 百度网盘链接&#xff1a;链接&#xff1a;https://pan.baidu.com/s/1VJ0G7W5AEQw8_MiagM7g8A?pwdg8…
阅读更多...
java线程生命周期介绍

java线程生命周期介绍

Java线程的生命周期包含以下几个状态&#xff1a; 1.新建(New)&#xff1a;线程对象被创建&#xff0c;但是还没有调用start()方法。 1.运行(Runnable)&#xff1a;线程正在运行或者是就绪状态&#xff0c;等待CPU时间片。 1.阻塞(Blocked)&#xff1a;线程暂时停止执行&…
阅读更多...
Nginx 精解：正则表达式、location 匹配与 rewrite 重写

Nginx 精解：正则表达式、location 匹配与 rewrite 重写

一、常见的 Nginx 正则表达式 在 Nginx 配置中&#xff0c;正则表达式用于匹配和重写 URL 请求。以下是一些常见的 Nginx 正则表达式示例&#xff1a; 当涉及正则表达式时&#xff0c;理解各个特殊字符的含义是非常重要的。以下是每个特殊字符的例子&#xff1a; ^&#xff1…
阅读更多...
修复损坏的Excel文件比你想象的要简单，这里提供几种常见的修复方法

修复损坏的Excel文件比你想象的要简单，这里提供几种常见的修复方法

打开重要的Excel文件时遇到问题吗？Microsoft Excel是否要求你验证文件是否已损坏？Excel文件可能由于各种原因而损坏，从而无法打开。但不要失去希望；你可以轻松修复损坏的Excel文件。 更改Excel信任中心设置 Microsoft Excel有一个内置的安全功能，可以在受限模式下打开有…
阅读更多...
Failed to start gdm.servide - GNOME Display manager

Failed to start gdm.servide - GNOME Display manager

启动虚拟机时&#xff0c;卡在Failed to start gdm.servide - GNOME Display manager不动。 解决方法: 1.重新启动Ubuntu&#xff0c;在进度条未结束之前&#xff0c;长按shift直到界面跳转到选项菜单。 2.选择第二个&#xff0c;按enter进入 3.选择最新版本&#xff08;后面…
阅读更多...
MySQL时间和日期类型详解（零基础入门篇）

MySQL时间和日期类型详解（零基础入门篇）

目录 1. DATE 2. DATETIME 3. TIMESTAMP 4. TIME 5. YEAR 6. 日期和时间的使用示例 以下SQL语句的测试可以使用命令行&#xff0c;或是使用SQL工具比如MySQL Workbench或SQLynx等。 在 MySQL 中&#xff0c;时间和日期数据类型用于存储与时间相关的数据&#xff0c;如何…
阅读更多...
摄影软件使用小技巧

摄影软件使用小技巧

记录摄影过程中使用一些软件的技巧&#xff0c;方便后续查阅。 摄影软件使用小技巧 Pr制作延时视频用PS批量转换RAW照片Lightroom批量处理照片月亮后期堆栈——RegiStax6 Pr制作延时视频 新建序列 选择需要的格式 用PS批量转换RAW照片 Lightroom批量处理照片 按 Shfit&#xf…
阅读更多...
解决Spark流处理产生的小文件问题

解决Spark流处理产生的小文件问题

做流批一体&#xff0c;湖仓一体的大数据架构&#xff0c;常见的做法就是&#xff1a; 数据源->spark Streaming->ODS&#xff08;数据湖&#xff09;->spark streaming->DWD&#xff08;数据湖&#xff09;->... 那么数据源->spark Streaming->ODS&…
阅读更多...
档案数字化管理的工具有哪些

档案数字化管理的工具有哪些

档案数字化管理的工具可以包括以下几种&#xff1a; 1. 扫描仪/数字拍摄仪&#xff1a;用于将纸质文件数字化为电子文件的工具。 2. OCR&#xff08;光学字符识别&#xff09;软件&#xff1a;用于将扫描或拍摄的图像文件转换为可编辑的文本文件。 3. 文件管理系统/专久智能电子…
阅读更多...
英语国际音标 - DJ 音标 - KK 音标

英语国际音标 - DJ 音标 - KK 音标

英语国际音标 - DJ 音标 - KK 音标 1. 国际音标 (International Phonetic Alphabet&#xff0c;IPA)1.1. 记音类型1.2. 48 个国际音标发音表1.2.1. 元音 (vowel)1.2.1.1. 单元音 (monophthong)1.2.1.2. 双元音 (diphthong) 1.2.2. 辅音 (consonant)1.2.2.1. 清音 (voiceless so…
阅读更多...
企业内网安全软件分享，有什么内网安全软件

企业内网安全软件分享，有什么内网安全软件

内网安全&#xff1f; 其实就是网络安全的一种。 什么是内网安全软件&#xff1f; 内网安全软件是企业保障内网安全的一种重要工具。 它主要帮助企业实现对网络设备、应用程序、用户行为等方面的监控和管理&#xff0c;以预防和应对各种网络攻击。 这类软件主要用于对内网中…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023