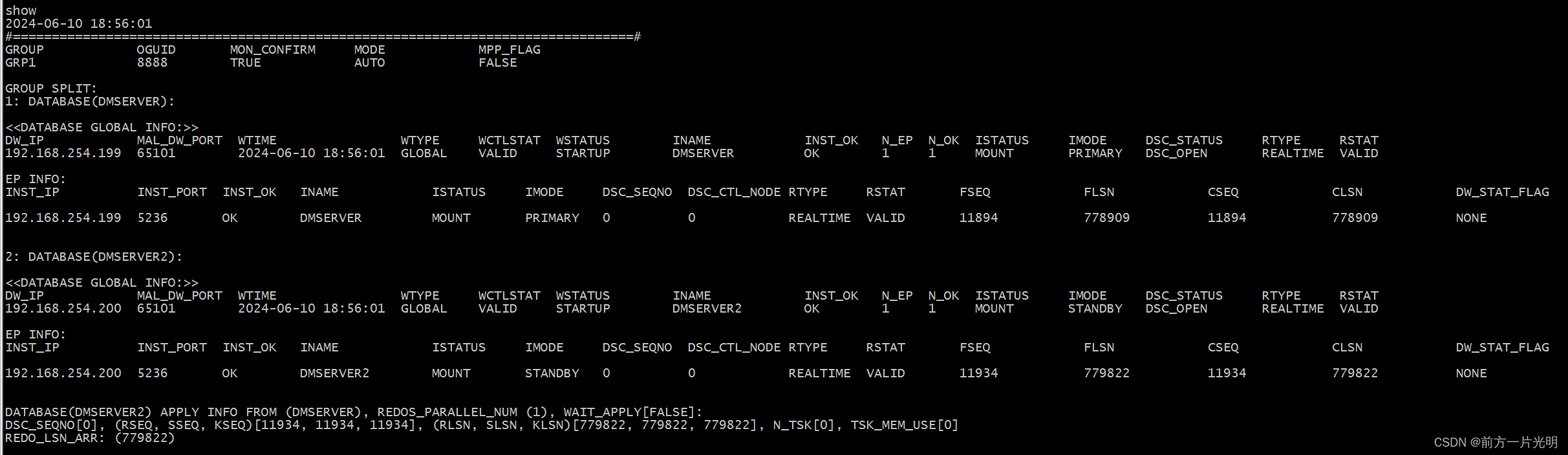
赵长鹏坐牢第一个月,越坐越富。
在币安联合创始人赵长鹏入狱服刑的第一个月,币安代币BNB创下了历史新高,使得赵长鹏成为美国联邦监狱中史上“最富囚犯”。与此同时,币安用户数量也到达2亿“里程碑”。
根据CoinGecko的数据,BNB的价格在周四达到了717.48美元的峰值,总市值上升至1090亿美元。自年初以来,该代币的价格已翻倍。

币安用户达2亿,代币BNB创新高
BNB 持有者可以在币安享受交易费折扣,该代币还被用于BNB智能链上的结算费。尽管去年经历了一段动荡期,BNB的市场主导表现依然十分稳固。
Kaiko的分析师Dessislava Aubert表示,从5月下旬的衍生品市场情况看,BNB的最近涨势是可以预见的,从6月开始,现货市场的需求开始增加,6月2日至5日期间,买盘持续超过卖盘。
Dessislava表示,BNB在十多个中心化交易所上市交易,“这与其他交易所的代币几乎只在其自家平台交易的情况不同”。她还补充说,币安占全球BNB交易量的85%。
在BNB的价格达到峰值之际,币安还创下了加密货币行业的另一项纪录。据媒体报道,币安托管的用户资产总额已从今年年初的大约800亿美元增长到目前的1250亿美元。
另外,该公司还在6月8日宣布,其全球用户数已达2亿。
加密货币市场的复苏推动币安交易量增加
去年11月21日,在美国证监会的压力下,币安向美方支付约43亿美元的罚款。同时,币安CEO赵长鹏承认违反了美国反洗钱法,宣布将辞去职位,并支付5000万美元罚款以了结相关指控。
不过,这对赵长鹏的财富影响甚微。据媒体估计,他的净资产为385亿美元,不过其财富的具体构成不明。赵长鹏在2021年接受美联社采访时表示,他的大部分财富都以BNB计价,并补充说,他是“币安的相当大股东”。
根据彭博亿万富翁指数,赵长鹏目前是世界上第40大富豪,他的净资产在2024年增长了41亿美元。
虽然赵长鹏从未公开过自己持有多少BNB,但根据BNB 2017年首次代币发行(ICO)的白皮书,创始团队获得了约8000万代币,如今的价值约为560亿美元。
苹果迈向AI新纪元:芯片、应用与大模型三线作战
一方面,需要开发能够在其设备上越来越多地支持AI功能的芯片,另一方面需要创建所谓的“杀手级”应用程序,吸引消费者,同时,还需要确保获得由竞争对手微软和谷歌控制的最先进的生成式AI模型。
在2023年的开发者大会上,苹果CEO蒂姆·库克发布了新款混合现实头戴设备Vision Pro,然而,对于彼时大热的生成式AI(Generative AI),苹果却保持了沉默。
一年后,谷歌和三星分别推出的Pixel 8和S24手机,引入了“AI智能手机”的新概念,微软、Meta和亚马逊等公司在生成式AI领域豪掷数十亿美元购置硬件设备,而苹果似乎仍然在“保持沉默”,引发了外界对苹果是否将错失技术转型机遇的担忧。
不过,随着万众瞩目的WWDC 2024到来,再次登上开发者大会舞台的库克有机会改变这一局面。市场预计,苹果将发布iOS 18操作系统,还将发布一系列AI服务和功能,标志着其生成式AI计划的开始。
媒体认为,当前库克面临巨大压力,迈向AI新纪元的苹果正面临着困难重重的“三线作战”——
一方面,需要开发能够在其设备上越来越多地支持AI功能的芯片,另一方面需要创建所谓的“杀手级”应用程序,吸引消费者,同时,还需要确保获得由竞争对手微软和谷歌控制的最先进的生成式AI模型。
摩根大通分析师Samik Chatterjee表示:
“苹果需要消除市场对其在生成式AI方面落后的看法,证明自己已赶上其他公司。”
芯片够强,但内存有挑战
芯片方面,媒体认为,苹果已经拥有足够强大的芯片来运行“人工智能智能手机”。自2017年以来,苹果一直拥有专用的神经网络架构,其最新的A17 Pro芯片在iPhone 15 Pro和Pro Max上超过了30 TOPS的基准。
这些带有神经网络引擎的NPU,使得在设备上本地运行一些极其计算密集的AI应用程序变得更容易,不过,它们也带来了“在内存方面巨大的技术挑战”,技术情报公司 ABI Research 的分析师 Reece Hayden 表示:
“即使是非常小的生成式AI模型,其内存需求也比目前任何手机都要高。”
目前,iPhone 15 Pro只有8GB的内存,而由高通芯片驱动的三星S24智能手机则有12GB。
另技术市场研究公司Counterpoint估计,“AI智能手机”将占到2027年全球智能手机出货量的43%,使用量将达到10亿台。
应用、大模型的战斗
应用方面,媒体认为,苹果可以采取的一个切实措施,是利用AI来增强Siri。
密歇根大学弗林特学院创新与技术学院的教授蒂姆·贝茨表示,在其现有硬件的限制范围内,苹果可以利用设备上保存的个人数据,为其用户打造这些个性化体验。
这种所谓的“端侧”还有一个额外的好处,就是保护用户的安全和隐私,因为消费者不太可能希望AI应用程序在其个人信息上进行训练并将其导出到云端。在本地运行功能还可以消除从远程服务器生成响应所涉及的延迟。贝茨补充称:
“Siri真的是交互式AI的完美‘风味’......个人可以控制他们的数据,与AI对话,完成任务,而不必担心数据会被吸走。”
美国银行的瓦姆西·莫汉认为,AI iPhone的杀手级应用,将在苹果能够提供一个“与设备上的一切完全集成,然后与云端的某种专家代理进行交互”的对话助手时出现。
这也是市场是预期苹果与OpenAI等公司的合作关系发挥作用的地方。虽然苹果一直在研发自己的生成模型,但它无法与基于数万亿数据参数的最先进模型相媲美,因此需要与其他公司达成协议。
这些举措可能使苹果与一些竞争对手持平,但尚未超越它们。在合作伙伴关系与进展的程度上,苹果与OpenAI之间的任何协议的具体轮廓尚不清楚。媒体分析称,这两家公司是否有文化契合点,以及这段“婚姻”能够持续多久,都是一个悬而未决的问题。
不过,专家们警告称,现在就排除苹果还为时过早。AI革命仍处于起步阶段,尚未有任何大型科技公司成功将生成式AI应用于杀手级硬件产品。 AMD的企业副总裁杰森·班塔表示:
“用体育的比喻来说,我认为我们还处于第一节的第一分钟...... 现在还为时过早。 ”