树状数组1

树状数组可以解决什么问题呢？
可以解决大部分区间上面的修改以及查询的问题，例如1.单点修改，单点查询，2.区间修改，单点查询，3.区间查询，区间修改，换言之，线段树能解决的问题，树状数组大部分也可以，但是并不一定都能解决，因为线段树的扩展性比树状数组要强.

为了更好的理解，下面咱们来看一道模板题点击跳转

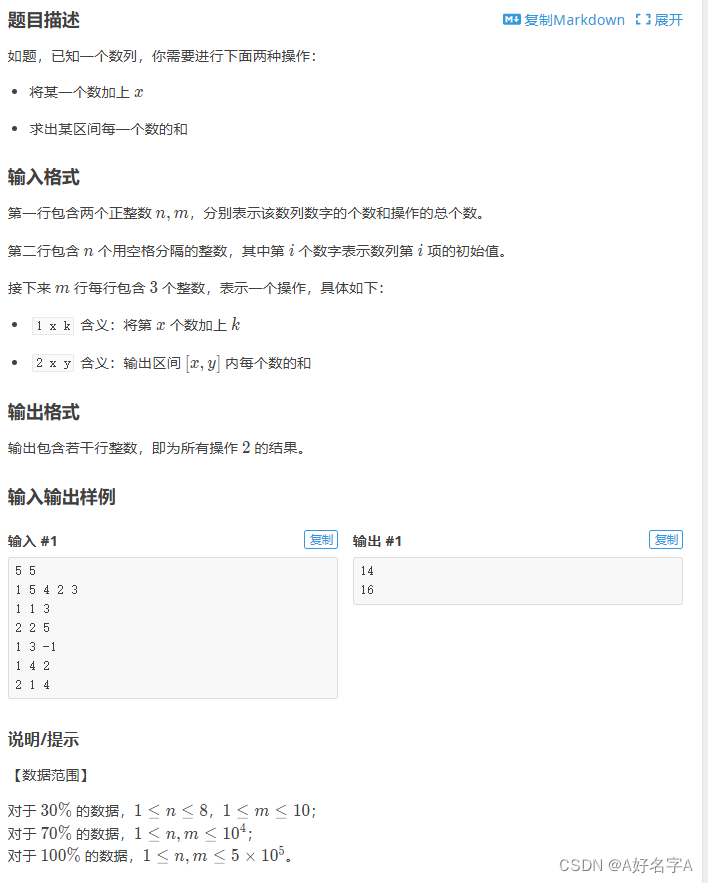
显然，我们一开始会想到暴力的朴素做法，单点修改操作时间复杂度O(1)，区间求和，暴力遍历区间每一个数再相加时间复杂度O(n)，如果区间求和查询的次数为n次，那么中的时间复杂度为$O(n^2)$,对于大数据的题来说肯定会TLE，此时如果用树状数组的话复杂度可以讲到$O(nlogn).$这时就要用到树状数组的奇妙了。
讲一些序列构建成树的形状，便于求和，便于增删，便于查找。
需要用到构建树状和查找结果两个函数，分别是

//构建函数
void add (int x,int y)
{
	while (x<=n)
	{
		a[x]+=y;
		x+=lowbit(x);
	}
}

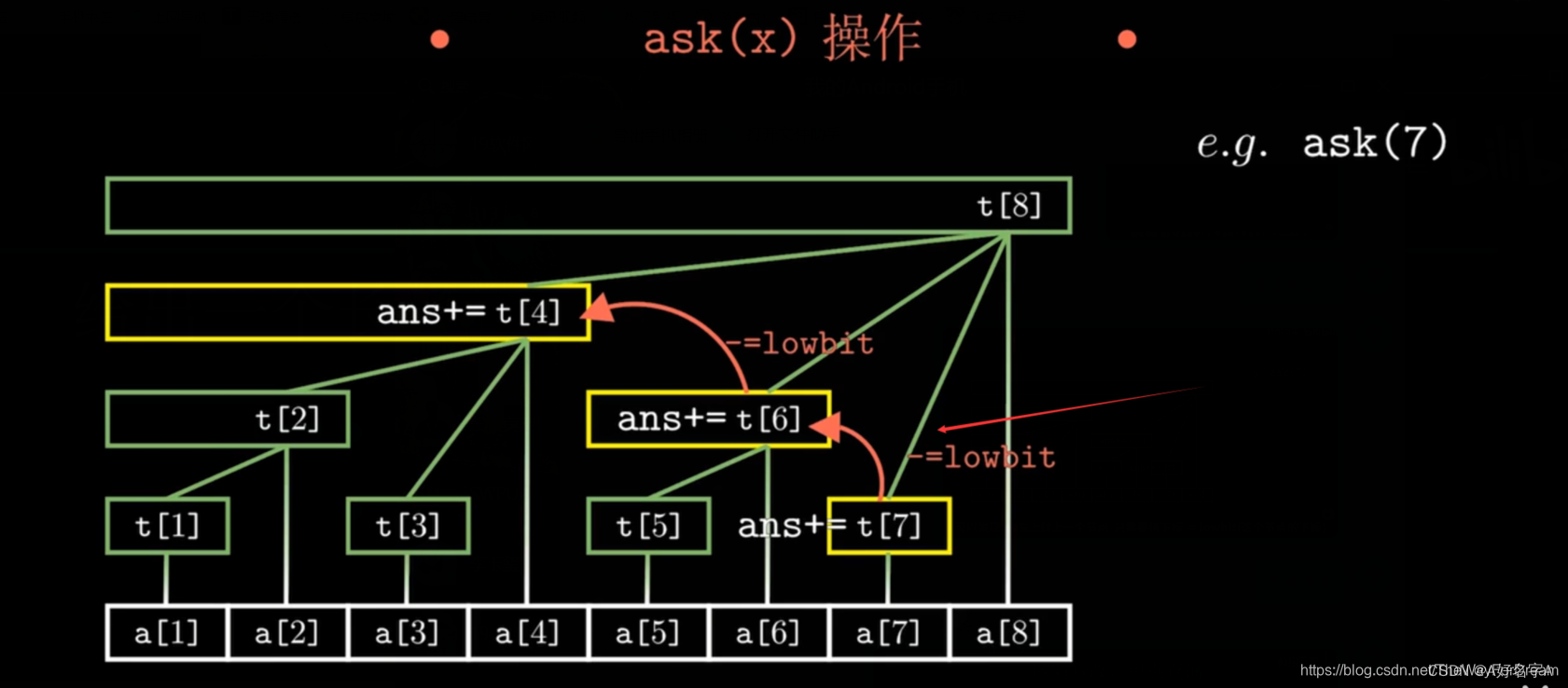
//查找函数
int search (int x)
{
	int ans=0;
	while (x)
	{
		ans+=a[x];
		x-=lowbit(x);
	}
	return ans;
}

有了这两个函数，就易如反掌了写这个题。
这里说一下lowbit lowbit() 函数用来 取一个二进制最低位的一与后边的0组成的数。可以用来判断一个数是不是2的幂次方，我们可以直接在头文件直接定义它。
接下来直接附上我的代码

#include<bits/stdc++.h>
#define int long long 
#define endl "\n"
#define fi first
#define se second
#define PII pair<int,int> 
#define lowbit(x) (x&(-x))
using namespace std;
const int N=2e6+5;
int a[N];
int n,m;
void add (int x,int y)
{
	while (x<=n)
	{
		a[x]+=y;
		x+=lowbit(x);
	}
}
int search (int x)
{
	int ans=0;
	while (x)
	{
		ans+=a[x];
		x-=lowbit(x);
	}
	return ans;
}

void solve()
{
	cin>>n>>m;
	for (int i=1;i<=n;i++)
	{
		int x;cin>>x;
		add(i,x);
	}
	for (int i=1;i<=m;i++)
	{
		int x,y,z;cin>>x>>y>>z;
		if (x==1) add(y,z);
		else 
		{
			cout<<search(z)-search(y-1)<<'\n';
		}
	}
	return ;
}
signed main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	int T=1;
	//cin >> T;
	while(T--) solve();
	return 0;
}

是一个树状数组的板子题，记住就可以了。

树状数组2

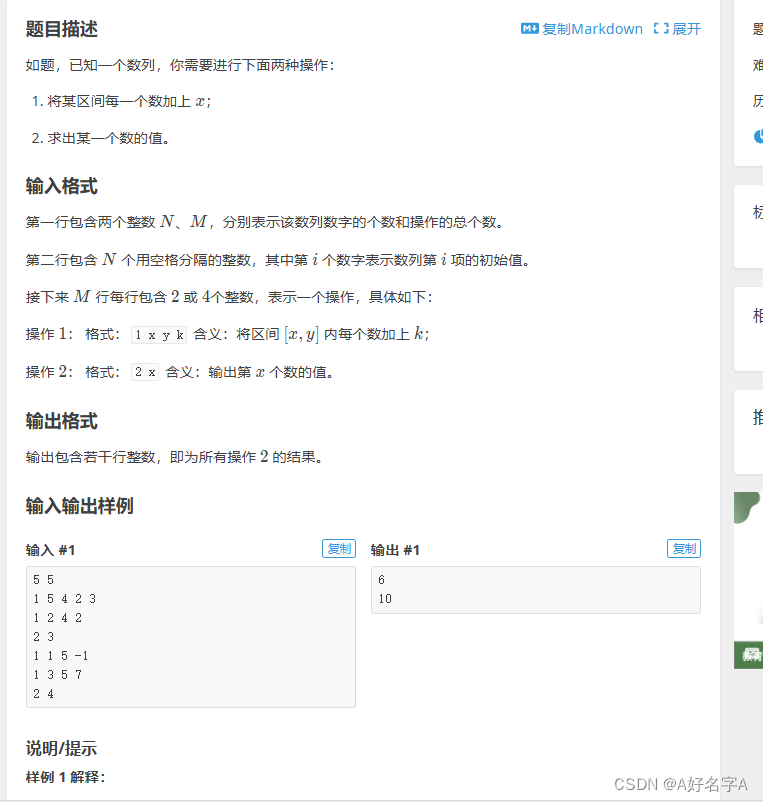
接下来是另一种树状数组的例题，基本思路和树状数组1大差不差，其中有些思路不一样，主要还是用到了上面所写的两个函数

#include<bits/stdc++.h>
#define int long long 
#define endl "\n"
#define fi first
#define se second
#define PII pair<int,int> 
#define lowbit(x) (x&(-x))
using namespace std;
const int N=1e6+5;
int a[N],c[N];
int n,m;
void add (int x,int y)
{
	while (x<=n)
	{
		c[x]+=y;
		x+=lowbit(x);
	}
}
int search (int x)
{
	int res=0;
	while (x)
	{
		res+=c[x];
		x-=lowbit(x);
	}
	return res;
}
void solve()
{
	cin>>n>>m;
	for (int i=1;i<=n;i++)
	{
		cin>>a[i];
		int x=a[i]-a[i-1];
		add(i,x);
	}
	for (int i=1;i<=m;i++)
	{
		int x;cin>>x;
	if (x==1)
	{
		int q,w,e;cin>>q>>w>>e;
		add(q,e);
		add(w+1,-e);
	}
	else if (x==2)
	{
		int cnt;cin>>cnt;
		cout<<search(cnt)<<'\n';
	}
	}
	
	return ;
}
signed main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	int T=1;
	//cin >> T;
	while(T--) solve();
	return 0;
}