94. 二叉树的中序遍历
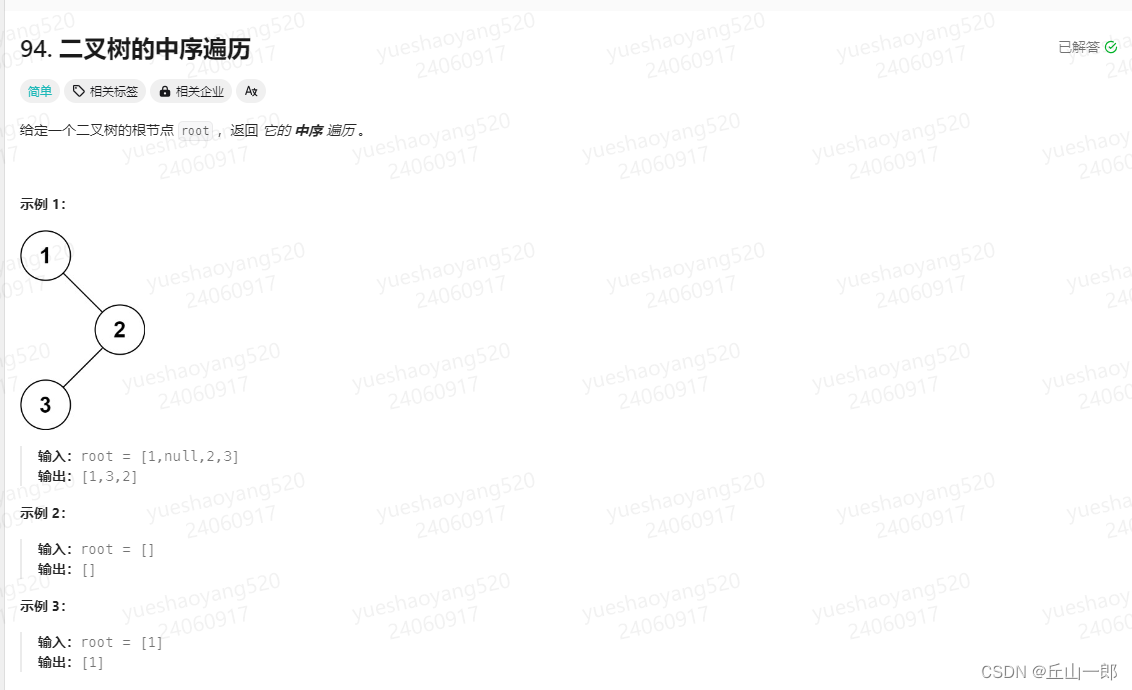
方法一:递归法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> arraylist=new ArrayList<>();
if(root==null){
return arraylist;
}
Stack<TreeNode> stack=new Stack<TreeNode>();
TreeNode current=root;
while(current!=null||!stack.isEmpty()){
while(current!=null){
stack.push(current);
current=current.left;
}
current=stack.pop();
arraylist.add(current.val);
current=current.right;
}
return arraylist;
}
}
方法二:迭代法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
// 中序遍历
List<Integer> res = new ArrayList<Integer>();
inorderTraversal(root, res);
return res;
}
public void inorderTraversal(TreeNode node, List<Integer> res) {
if (node == null) {
return;
}
inorderTraversal(node.left, res);
res.add(node.val);
inorderTraversal(node.right, res);
}
}
104. 二叉树的最大深度
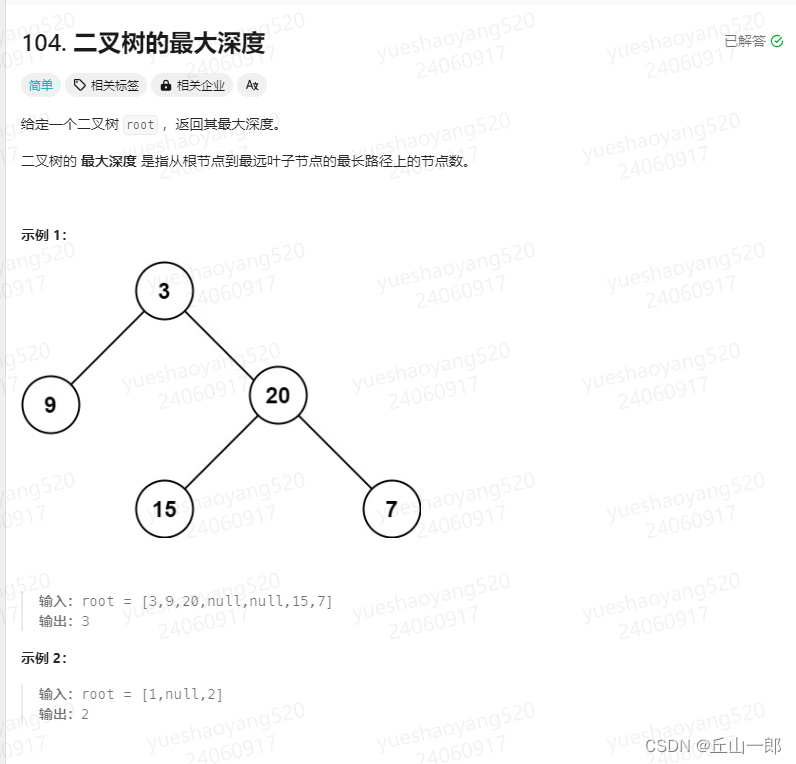
方法一:递归方法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
if(root==null){
return 0;
}else {
int leftLength = maxDepth(root.left)+1;
int rightLength = maxDepth(root.right)+1;
return Math.max(leftLength,rightLength);
}
}
}
方法二:层序遍历
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int ans = 0;
int size = 0;
LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
queue.add(root);
while (!queue.isEmpty()) {
size = queue.size();
while (size > 0) {
root = queue.poll();
if (root.left != null) {
queue.offer(root.left);
}
if (root.right != null) {
queue.offer(root.right);
}
size--;
}
ans++;
}
return ans;
}
}
226. 翻转二叉树
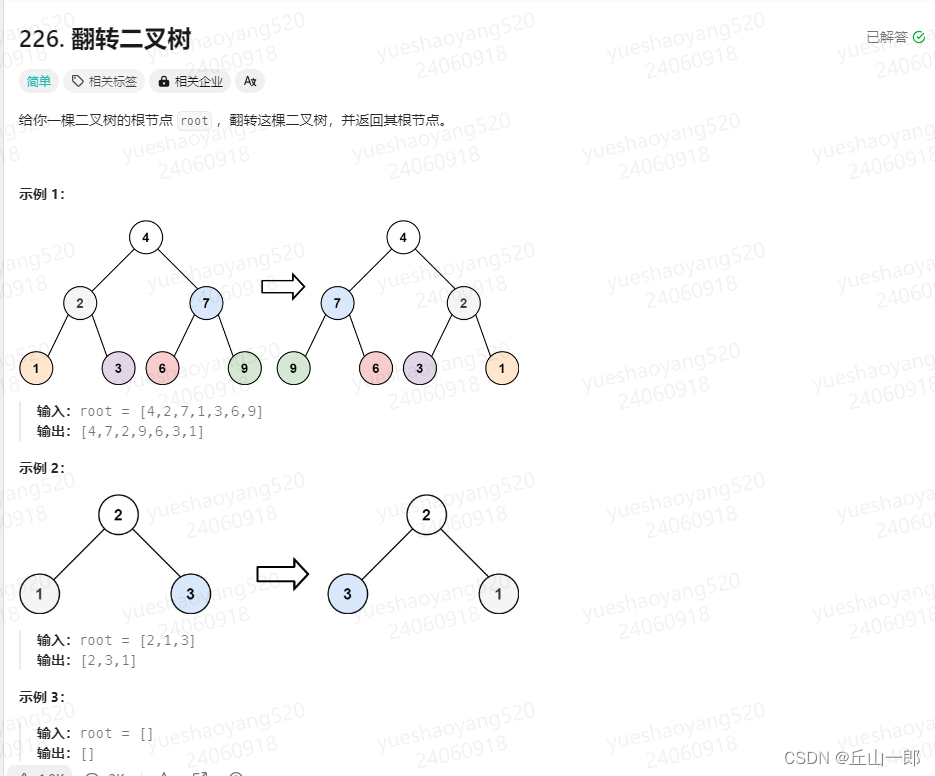
方法一:递归
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
if(root==null){
return 0;
}else {
int leftLength = maxDepth(root.left)+1;
int rightLength = maxDepth(root.right)+1;
return Math.max(leftLength,rightLength);
}
}
}
方法二:迭代
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
TreeNode node = root;
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.add(node);
int size = 0;
while (!queue.isEmpty()) {
size = queue.size();
while (size > 0) {
TreeNode temp = queue.poll();
TreeNode left = temp.left;
if (left != null) {
queue.offer(left);
}
TreeNode right = temp.right;
if (right != null) {
queue.offer(right);
}
temp.left = right;
temp.right = left;
size--;
}
}
return root;
}
}
101. 对称二叉树
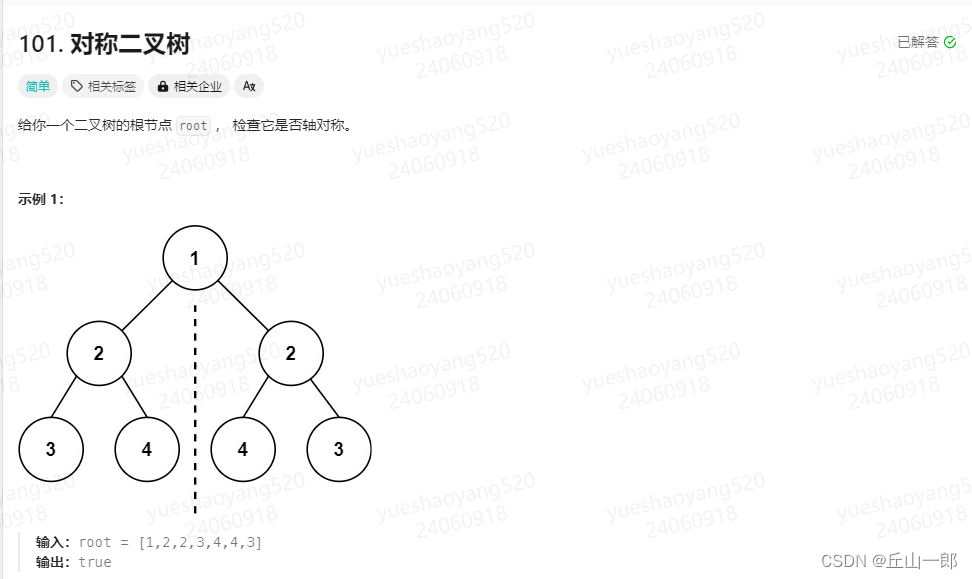
方法一:递归
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null) {
return true;
}
return isSymmetric(root.left,root.right);
}
public boolean isSymmetric(TreeNode left,TreeNode right) {
if(left==null&&right==null){
return true;
}
if(left==null|| right==null){
return false;
}
if(left.val!=right.val){
return false;
}
return isSymmetric(left.left,right.right)&& isSymmetric(left.right,right.left);
}
}
方法二:迭代
class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null) {
return true;
}
return isSymmetric(root.left, root.right);
}
public boolean isSymmetric(TreeNode left, TreeNode right) {
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(left);
queue.offer(right);
while (!queue.isEmpty()) {
left = queue.poll();
right = queue.poll();
if (left == null && right == null) {
continue;
}
if (left == null || right == null || left.val != right.val) {
return false;
}
queue.offer(left.left);
queue.offer(right.right);
queue.offer(left.right);
queue.offer(right.left);
}
return true;
}
}
543. 二叉树的直径
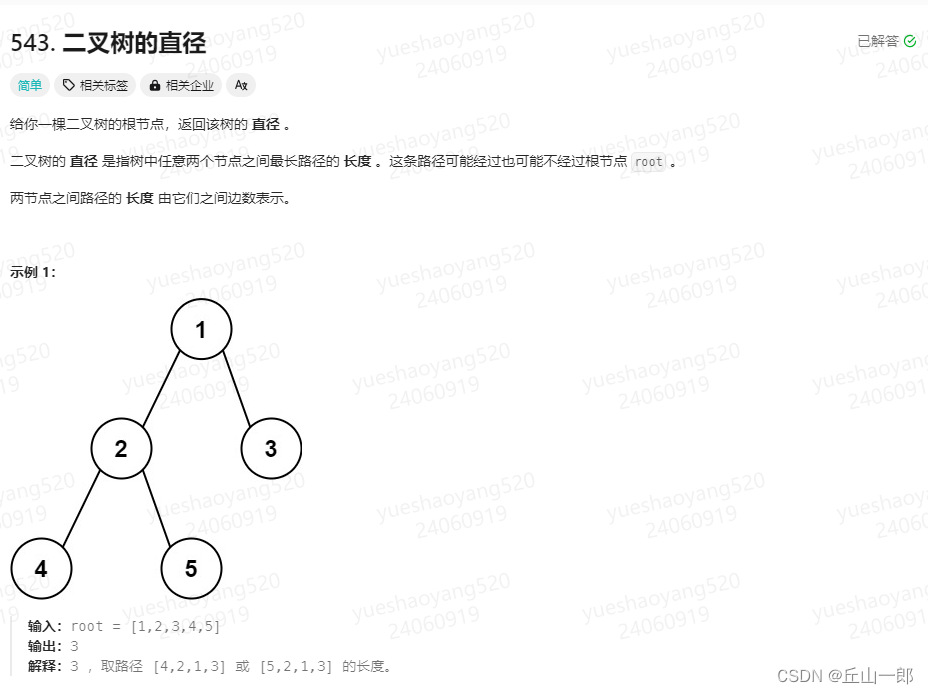
方法一:递归
class Solution {
int ans = 0;
public int diameterOfBinaryTree(TreeNode root) {
diameterOfBinaryTreePLus(root);
return ans;
}
public int diameterOfBinaryTreePLus(TreeNode root) {
if(root==null){
return 0;
}
int left = diameterOfBinaryTreePLus(root.left);
int right = diameterOfBinaryTreePLus(root.right);
ans = Math.max(ans,left+right);
return Math.max(left+1,right+1);
}
}
102. 二叉树的层序遍历
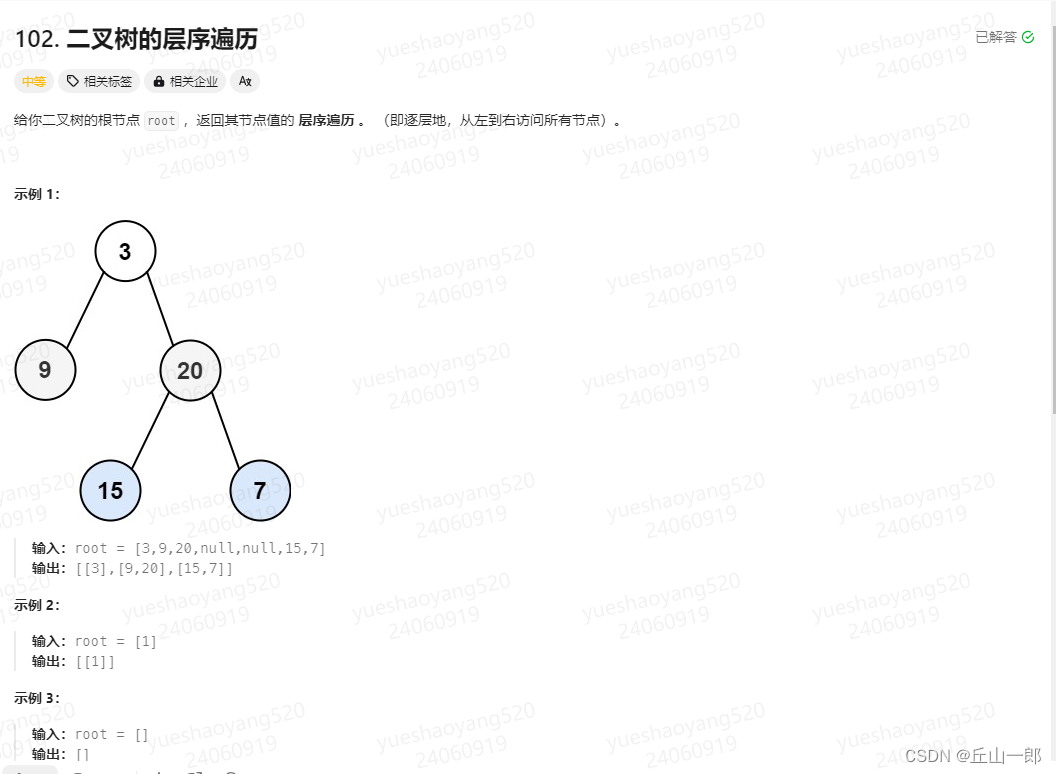
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> result = new ArrayList<List<Integer>>();
if (root == null) {
return result;
}
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root);
int size = 0;
while (!queue.isEmpty()) {
size = queue.size();
List<Integer> list = new ArrayList<Integer>();
while (size > 0) {
TreeNode node = queue.poll();
list.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
size--;
if (size == 0) {
result.add(list);
}
}
}
return result;
}
}
108. 将有序数组转换为二叉搜索树
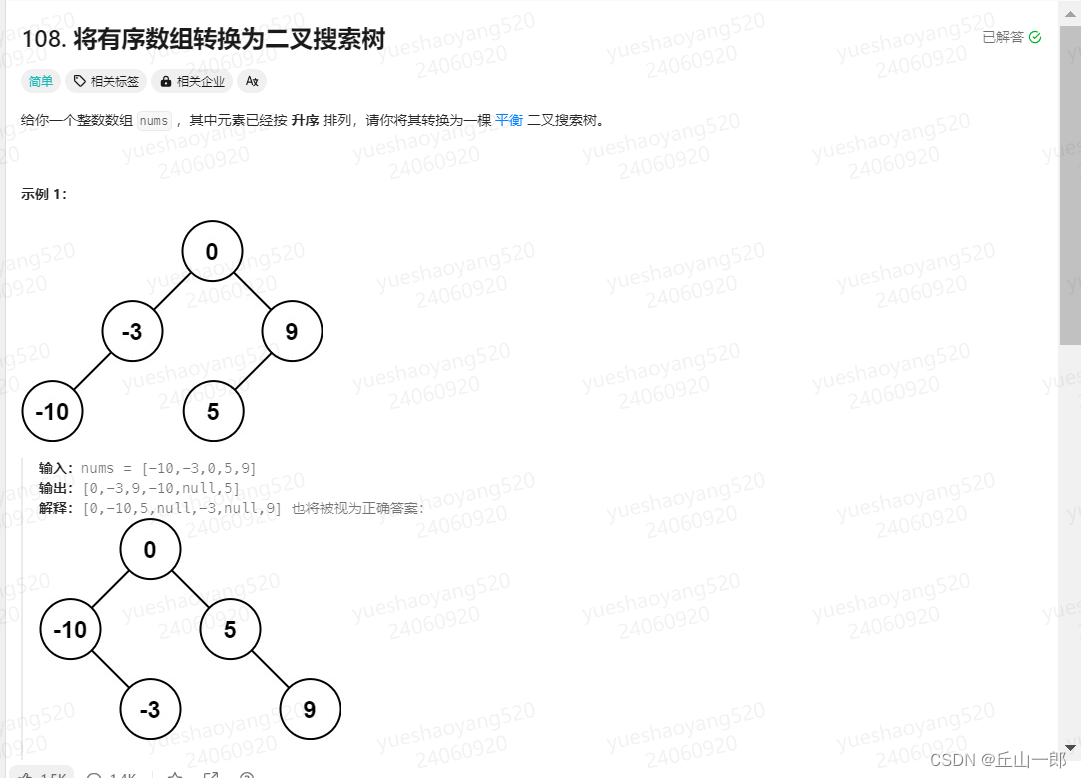
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return sortedArrayToBST(nums,0,nums.length-1);
}
public TreeNode sortedArrayToBST(int[] nums,int left,int right){
if(left>right){
return null;
}
int mid = (left+right)/2;
TreeNode root = new TreeNode(nums[mid]);
root.left = sortedArrayToBST(nums,left,mid-1);
root.right = sortedArrayToBST(nums,mid+1,right);
return root;
}
}
98. 验证二叉搜索树
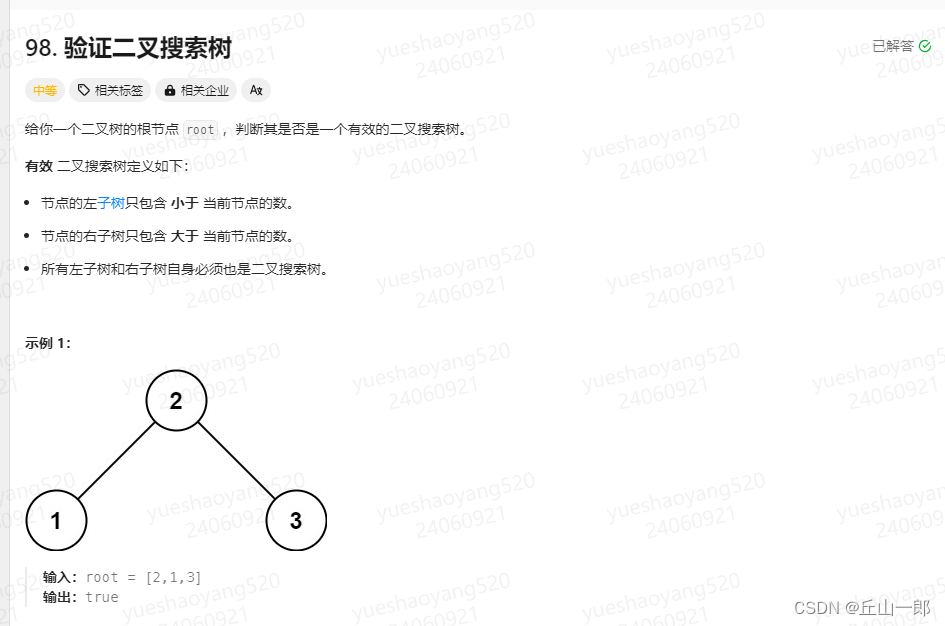
方法一:递归
初始错误写法
class Solution {
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
if (root.left != null) {
if (root.left.val >= root.val) {
return false;
}
}
if (root.right != null) {
if (root.right.val <= root.val) {
return false;
}
}
boolean left = isValidBST(root.left);
boolean right = isValidBST(root.right);
return left && right;
}
}
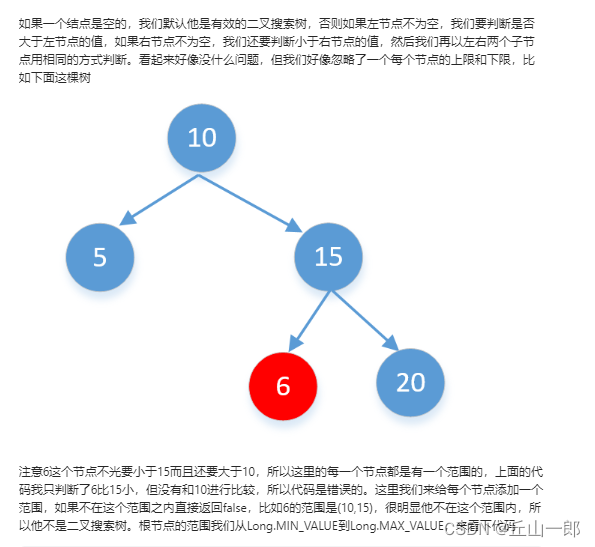
正确写法
/**
* Definition for a binary tree node.
* public class TreeNode {
* long val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(long val) { this.val = val; }
* TreeNode(long val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
return isValidBSTPlus(root,Long.MIN_VALUE,Long.MAX_VALUE);
}
public boolean isValidBSTPlus(TreeNode root,long min,long max) {
if (root == null) {
return true;
}
if (root.left != null) {
if (root.left.val >= root.val) {
return false;
}
}
if (root.right != null) {
if (root.right.val <= root.val) {
return false;
}
}
if(root.val>=max || root.val<=min){
return false;
}
boolean left = isValidBSTPlus(root.left,min,root.val);
boolean right = isValidBSTPlus(root.right,root.val,max);
return left && right;
}
}
方法二:中序遍历
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isValidBST(TreeNode root) {
long limit = Long.MIN_VALUE;
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode currentNode = root;
while (currentNode != null || !stack.isEmpty()) {
while (currentNode != null) {
stack.push(currentNode);
currentNode = currentNode.left;
}
currentNode = stack.pop();
if (currentNode.val <= limit) {
return false;
}
limit = currentNode.val;
currentNode = currentNode.right;
}
return true;
}
}










![[Cloud Networking] Layer 2](https://img-blog.csdnimg.cn/img_convert/ae778f4d1be9c7891bdf05ac5f63e640.webp?x-oss-process=image/format,png)