树与二叉树基础部分
- 树的基础概念
- 二叉树的性质
- 二叉树的遍历
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
- 根据遍历结果恢复二叉树
- 二叉树的创建
- 第一种
- 第二种
- 二叉树的其他典型操作
- 查找指定元素(一般二叉树)
- 二叉树的高度(深度)
- 二叉树的拷贝
- 二叉树的销毁
- 二叉树的节点个数
- 第k层的节点个数
- 二叉树叶子结点个数
- 搜索二叉树
- 逐点插入法
- 查找
- 到指定节点的路径
树的基础概念
一、树的特点:
1.有且仅有一个节点没有前驱结点,即根结点;
2.除了根结点外,每个结点有且仅有一个直接前驱结点;
3.包括根结点在内,每个结点可以有多个后继结点。
二、基本术语名词
结点的度:该结点拥有的子树的数目。
树的度:树中结点度的最大值。
叶结点:度为0的结点。
分支节点:度非0的结点。
树的层次:根结点为第1层,若某层节点在第i层,则其孩子结点(若存在)为第i+1层。
树的深度/高度:树中结点所处的最大层次数。
路径:路径长度等于路径结点树-1.路径是从di到dj结点的一条结点序列。从根结点到树中其余结点均分别存在一条唯一路径。
祖先与子孙:一个结点的祖先是从根结点到该结点路径上所经过的所有结点;而一个结点的子孙则是以该结点为根的子树上的所有其他结点。
森林:m>=0颗不想交的树组成的树的集合。
判断:
1.度为2的树是二叉树?(×)
2.度为2的有序树是二叉树?(×)
图中没有区分左右子树,不是二叉树。
结论:子树有严格的左右之且度<=2的树是二叉树。
注意:具有三个节点的二叉树有几种形态?
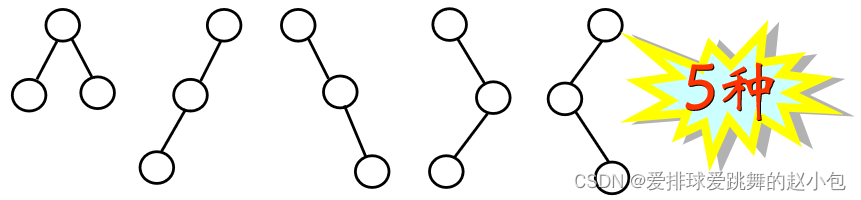 具有三个结点的树有几种形态?
具有三个结点的树有几种形态?
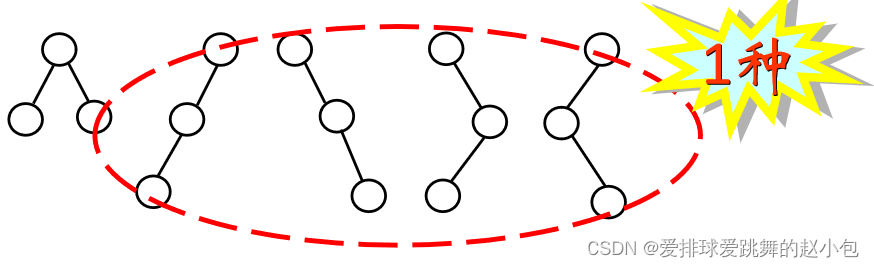
二叉树的性质
1.具有n个结点的非空二叉树共有n-1个分支(边)。
2.非空二叉树的第i层最多有2^(i-1)个结点。(i>=0)
3.深度为h的非空二叉树最多有2^h-1个结点。
4.若非空二叉树有n0个叶结点,有n2个度为2的结点,则n0=n2+1。
证明:
n=n0+n1+n2
设分支数目为B,则根据性质1:
B=n-1
这些分支来自于度为1和度为2的结点:
B=n1+2n2
则根据2和3式:n-1=n1+2n2
即n=1+n1+2n2
=n0+n1+n2
因此:n0=n2+1
推论:n0=n2+2n3+3n4+……+(m-1)nm+1
5.具有n个结点的非空完全二叉树的深度为:h=logn+1;
6.顺序存储结构中:结点i的父节点编号:(i-1)/2;
结点i的左孩子结点:2i+1;右孩子:2i+2;
数组存储方式只适用于完全二叉树和满二叉树,其他二叉树会造成内存的浪费。
二叉树的遍历
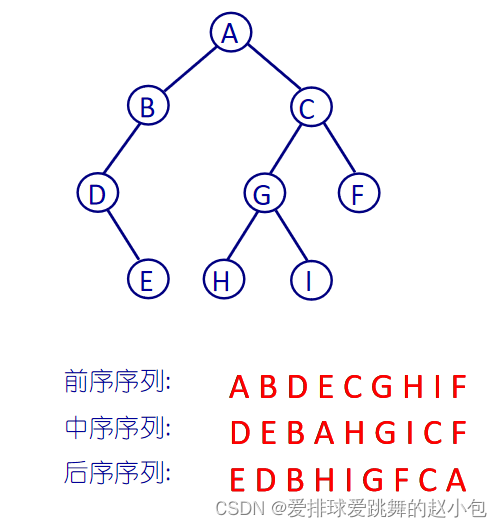 树的遍历一般是说在链式结构下的遍历,那么此时我们需要定义一个结构体:
树的遍历一般是说在链式结构下的遍历,那么此时我们需要定义一个结构体:
typedef struct node
{
int val;
struct node* left;
struct node* right;
}BTNode;
typedef BTNode* BTNodeptr;
前序遍历
void Preorder(BTNodeptr t)
{
if(t==NULL)
return;
visit(t);//访问结点t
Preorder(t->left);
Preorder(t->right);
}
中序遍历
void Inorder(BTNodeptr t)
{
if(t==NULL)
return;
Inorder(t->left);
visit(t);
Inorder(t->right);
}
后序遍历
void Postorder(BTNodeptr t)
{
if(t==NULL)
return;
Postorder(t->left);
Postorder(t->right);
visit(t);
}
前中后序遍历都是深度优先遍历(DFS),而接下来的层序遍历则是广度优先遍历(BFS);
层序遍历
这种遍历方法没有用到递归,而是使用了一个队列:
方法是:从根结点开始,父节点先入队列,再出队列并输出,同时将父节点的两个子节点(若存在)入队。再取出队头元素,同时将队头元素的两个子节点(若存在)入队。直至队列为空,输出的序列就是层序遍历的结果啦~
#define MAX 100
void Treeorder(BTNodeptr t)
{
BTNode* queue[MAX];
int Front=0;
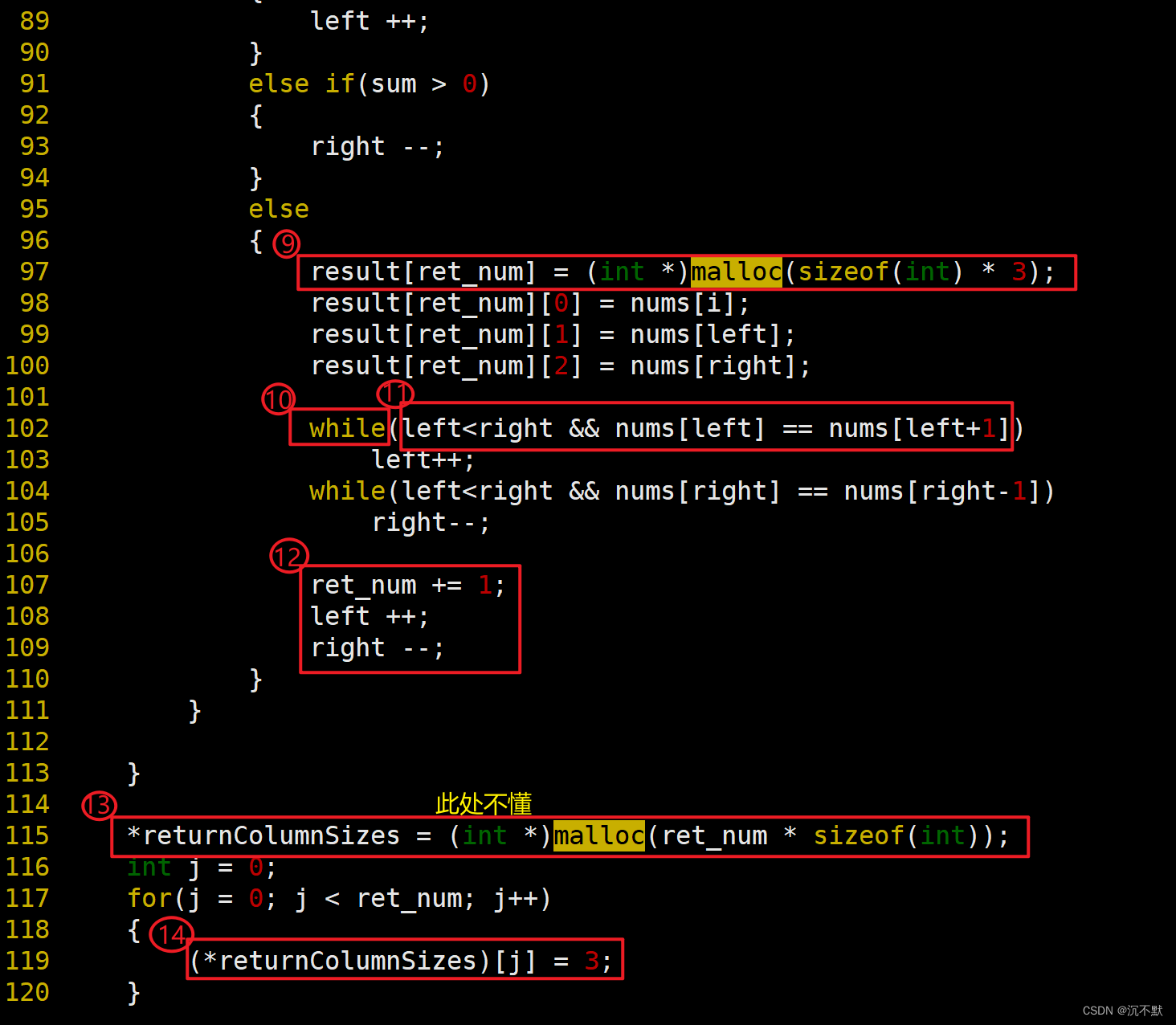
int Rear=MAX-1;
int Count=0;
if(t)
{
Rear=(Rear+1)%MAX;
queue[Rear]=t;
Count++;
}
BTNode* front;
while(Count!=0)
{
front=queue[Front];
Front=(Front+1)%MAX;
Count--;
visit(front);
if(front->left)
{
Rear=(Rear+1)%MAX;
queue[Rear]=front->left;
Count++;
}
if(front->right)
{
Rear=(Rear+1)%MAX;
queue[Rear]=front->right;
Count++;
}
}
}
根据遍历结果恢复二叉树
前序+中序(√)
后序+中序(×)
前序+后序(×)
因为前序和后序分别一致的两颗树,也有可能结构不同,比如:
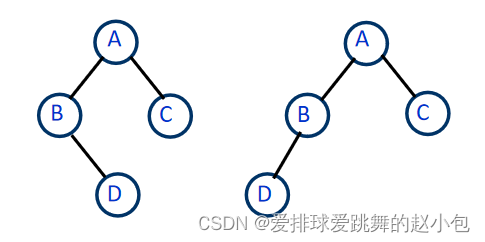
两颗树前序序列都为:ABDC
后序序列都为DBCA,
但很明显,结构不一样
已知前(后)序序列和中序序列,恢复二叉树:
在前(后)序序列中确定根,在中序序列中区分左右。
二叉树的创建
第一种
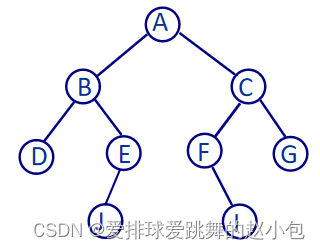
输入:A B D ^ ^ E J ^ ^ ^ C F ^ I ^ ^ G ^ ^
第一个字符表示根结点字符,后面的每一个字符表示前面字符的孩子结点字符,先输入的是左孩子,后输入右孩子,^表示没有孩子。
那么如何根据上述输入构造出如下的二叉树呢?
这个输入是一个前序遍历结果,那创建这个树的思想其实也是前序创建,也就是说访问到一个值,那么先创建这个子树的根结点,再创建它的左子树节点,再创建右子树结点,直到遇到^,返回NULL即可。
伪代码体现:
读入字符ch
if(ch==‘^’)
不创建结点,返回NULL
else
创建子树根结点
创建该根结点的左子树
创建该根结点的右子树
这是创建好树以后,按照前中后序遍历打印结果:

BTNodeptr createtree();
int main()
{
BTNodeptr root;
root=createtree();
Preorder(root);
printf("\n");
Inorder(root);
printf("\n");
Postorder(root);
return 0;
}
BTNodeptr createtree()
{
BTNodeptr p;
char ch;
ch=getchar();
if(ch=='^')
return NULL;
else
{
p=(BTNodeptr)malloc(sizeof(BTNodeptr));
p->val=ch;
p->left=createtree();
p->right=createtree();
return p;
}
}
第二种
输入:
5
ABC
BDE
CFG
EJ^
F^I
先输入分支节点个数(非叶子结点),按层次从左到右依次输入父节点和孩子结点,若孩子结点不存在,则以^字符表示
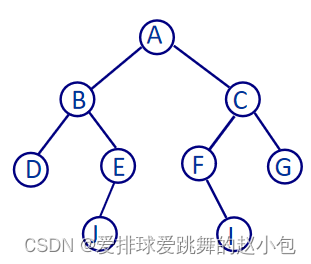
那么如何根据上述输入构造如下二叉树呢?
我们有两种方法来解决:第一种用到队列,思想类似于层序遍历,因为输入形式为:根 左 右,因此根入队,根再出队,根的左右子节点入队;输入下一行时,判断队头是不是这一行的第一个字符,如果不是,说明队头元素是一个叶子结点;如果是,那么队头出队,这一行的后两个元素入队(非^时入队),并且链接到队头元素的左右子树上。
BTNodeptr createtree1();
int main()
{
BTNodeptr root;
root=createtree1();
Preorder(root);
printf("\n");
Inorder(root);
printf("\n");
Postorder(root);
return 0;
}
BTNodeptr createtree1()
{
BTNodeptr root=NULL;
BTNodeptr queue[MAX];
BTNodeptr p=NULL;//这个用于取队头元素
int Front=0,Rear=MAX-1;
char str[4];//存储每一行输入的三个元素
int n;
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%s",str);
if(root==NULL)
{
root=(BTNodeptr)malloc(sizeof(BTNode));
root->val=str[0];
root->left=NULL;
root->right=NULL;
p=root;
}
else//这一步用于找头结点
{
do
{
p=queue[Front];
Front=(Front+1)%MAX;
} while (p->val!=str[0]);
}
if(str[1]!='^')
{
p->left=(BTNodeptr)malloc(sizeof(BTNode));
p->left->left=NULL;
p->left->right=NULL;
p->left->val=str[1];
Rear=(Rear+1)%MAX;
queue[Rear]=p->left;
}
if(str[2]!='^')
{
p->right=(BTNodeptr)malloc(sizeof(BTNode));
p->right->left=NULL;
p->right->right=NULL;
p->right->val=str[2];
Rear=(Rear+1)%MAX;
queue[Rear]=p->right;
}
}
return root;
}

后三行为按照前中后序遍历输出的结果↑。
BUT/HOWEVER/NEVERTHELESS……!!!!这种方法存在一个很大的缺陷就是:
输入的时候只能按照层序来,也就是说,刚刚我们的输入顺序是:
ABC
BDE
CFG
EJ^
F^I
一旦这个顺序发生变化,这种算法就没办法实现了,比如:
ABC
CFG
F^I
BDE
EJ^
为什么不可以呢?原因就在于队列。当我们读入第一行后,队列中的元素为:
 读第二行是时,我们发现队头元素不是C,于是继续向后查找,发现第二个元素是C,然后将C出队,C的子节点入队:
读第二行是时,我们发现队头元素不是C,于是继续向后查找,发现第二个元素是C,然后将C出队,C的子节点入队:
 我们此时发现:B出队,但是在输入的第四行,还有B!但是此时B已经不在队列里了。因此,如果输入子树的顺序不是按照层序顺序来进行,那就需要另外定义一个查找函数find,用于在已经构建好的树中查找父节点。
我们此时发现:B出队,但是在输入的第四行,还有B!但是此时B已经不在队列里了。因此,如果输入子树的顺序不是按照层序顺序来进行,那就需要另外定义一个查找函数find,用于在已经构建好的树中查找父节点。
BTNodeptr createtree2();
BTNodeptr find(BTNodeptr root,char ch);
int main()
{
BTNodeptr root;
root=createtree2();
Preorder(root);
printf("\n");
Inorder(root);
printf("\n");
Postorder(root);
return 0;
}
BTNodeptr createtree2()
{
BTNodeptr root=NULL;
BTNodeptr p=NULL;//这个用于表示每一步的父节点
char str[4];//存储每一行输入的三个元素
int n;
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%s",str);
if(root==NULL)
{
root=(BTNodeptr)malloc(sizeof(BTNode));
root->val=str[0];
root->left=NULL;
root->right=NULL;
p=root;
}
else//这一步用于找头结点
{
p=find(root,str[0]);
}
if(str[1]!='^')
{
p->left=(BTNodeptr)malloc(sizeof(BTNode));
p->left->left=NULL;
p->left->right=NULL;
p->left->val=str[1];
}
if(str[2]!='^')
{
p->right=(BTNodeptr)malloc(sizeof(BTNode));
p->right->left=NULL;
p->right->right=NULL;
p->right->val=str[2];
}
}
return root;
}
BTNodeptr find(BTNodeptr root,char ch)
{
BTNodeptr p=NULL;
if(root!=NULL)
{
if(root->val==ch)
p=root;
else
{
p=find(root->left,ch);
if(p==NULL)
p=find(root->right,ch);
}
}
return p;
}
改进的地方,就是把找每一行头结点的那一步,从在队列里找,变成了在已有的树中找。同时,find函数也是一个比较基础的树操作,大致和中序遍历的思想一致,先判断头结点的值是否和要找的字符一致,如果不一致,再在左子树里找,如果没找到,再在右子树里找。

二叉树的典型操作有很多:
检查二叉树是否为空
在二叉树中查找给定元素
获得二叉树中包含给定元素路径
在二叉树中插入一个元素
从二叉树中删除一个元素
获得二叉树的高度
获得二叉树的节点数目
获得二叉树叶节点的数目
遍历二叉树
拷贝二叉树
删除二叉树
现在现在这里介绍加粗的这几种,剩下的插入、删除、结点路径这几种留在一会儿的搜索二叉树(二叉查找树)中介绍。
二叉树的其他典型操作
查找指定元素(一般二叉树)
BTNodeptr find(BTNodeptr root,char ch)
{
BTNodeptr p=NULL;
if(root!=NULL)
{
if(root->val==ch)
p=root;
else
{
p=find(root->left,ch);
if(p==NULL)
p=find(root->right,ch);
}
}
return p;
}
二叉树的高度(深度)
int height(BTNodeptr p)
{
if(p==NULL)
return 0;
else return 1+max(height(p->left),height(p->right));
}
二叉树的拷贝
BTNodeptr copy(BTNodeptr src)
{
BTNodeptr obj;
if(src==NULL)
obj=NULL;
else
{
obj=(BTNodeptr)malloc(sizeof(BTNode));
obj->val=src->val;
obj->left=copy(src->left);
obj->right=copy(src->right);
}
return obj;
}
拷贝的时候按照前中后序拷贝都可以,但是二叉树销毁,就必须按照后序了:
二叉树的销毁
void destroy(BTNodeptr p)
{
if(p!=NULL)
{
destroy(p->left);
destroy(p->right);
free(p);
p=NULL;
}
}
二叉树的节点个数
int TreeSize(BTNodeptr root)
{
return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
}
第k层的节点个数
可以先拆解一下问题:
递归子问题:
第k层结点个数=左子树第k-1层结点个数+右子树第k-1层结点个数
最小子问题:
遍历到空节点:返回0;该结点不为空但是该结点是叶子结点即k==1
int levelnum(BTNodeptr p,int k)
{
if(p==NULL)
return 0;
if(p!=NULL&&k==1)
return 1;
return levelnum(p->left,k-1)+level(p->right,k-1);
}

以这一棵树为例,我们测试一下各个层的节点个数:
 完全正确。
完全正确。
二叉树叶子结点个数
这个题和上一道题趋同,我们先来分解一下问题:
遍历到空节点:返回0
遍历到叶子结点(左右子树都为NULL):返回1
叶子结点个数=左子树的叶子节点个数+右子树的叶子结点个数
写起来:
int leaf(BTNodeptr root)
{
if(root==NULL)
return 0;
if(root->left==NULL&&root->right==NULL)
return 1;
return leaf(root->left)+leaf(root->right);
}
还是刚刚那个二叉树,我们检测一下叶子结点个数对不对:
 完全正确。
完全正确。
搜索二叉树
也叫二叉查找树,特点为:
若根结点的左子树不空,则左子树上所有结点都小于根结点;若右子树不为空,则右子树上结点值都小于根结点。每一颗子树上也符合上述特点。
逐点插入法
利用这个方法可以建立起搜索二叉树,核心在于和根结点比较,值比根结点大,往右子树插入,比根结点小,插到左子树,相等的话,根据具体情况做具体操作。
现可用递归和非递归两种方式来构建逐点插入法:
递归:
BTNodeptr insert(BTNodeptr p,int item);
int main()
{
BTNodeptr root=NULL;
int i,item;
for(i=0;i<10;i++)
{
scanf("%d",&item);
root=insert(root,item);
}
Inorder(root);
printf("\n");
return 0;
}
BTNodeptr insert(BTNodeptr p,int item)
{
if(p==NULL)
{
p=(BTNodeptr)malloc(sizeof(BTNode));
p->val=item;
p->left=p->right=NULL;
}
else if(item<p->val)
{
p->left=insert(p->left,item);
}
else if(item>p->val)
{
p->right=insert(p->right,item);
}
else{
//如果相等,根据具体要求做。
}
return p;
}
看看测试结果:

按照中序遍历输出,序列递增。
非递归:
void insert1(int item);
BTNodeptr root=NULL;
int main()
{
int i,item;
for(i=0;i<10;i++)
{
scanf("%d",&item);
insert1(item);
}
Inorder(root);
printf("\n");
return 0;
}
void insert1(int item)
{
BTNodeptr new=(BTNodeptr)malloc(sizeof(BTNode));
new->val=item;
new->left=new->right=NULL;
if(root==NULL)
{
root=new;
return;
}
BTNodeptr cur=root;
while(1)
{
if(item<cur->val)
{
if(cur->left==NULL)
{
cur->left=new;
break;
}
else
cur=cur->left;
}
else if(item>cur->val)
{
if(cur->right==NULL)
{
cur->right=new;
break;
}
else
cur=cur->right;
}
else
{
//具体情况具体判断
}
}
return;
}
真心建议各位朋友都用非递归,调试起来也更方便明了,递归的话,调试的时候你的脑子是真跟不上F11的跳跃……
查找
BTNodeptr search(BTNodeptr p,int n)
{
BTNodeptr cur=p;
while(cur!=NULL)
{
if(n>cur->val)
cur=cur->right;
else if(n<cur->val)
cur=cur->left;
else
return cur;
}
return NULL;
}
到指定节点的路径
搜索二叉树和普通二叉树的这个算法区别还是很大的,因为搜索二叉树的特殊性质:
搜索二叉树:
void searchBST(BTNodeptr p,int n)
{
BTNodeptr cur=p;
while(cur!=NULL)
{
if(n>cur->val)
{
printf("%d ",cur->val);
cur=cur->right;
}
else if(n<cur->val)
{
printf("%d ",cur->val);
cur=cur->left;
}
else
{
printf("%d ",cur->val);
break;
}
}
}
在主函数中测试一下:
void searchBST(BTNodeptr p,int n);
BTNodeptr root=NULL;
int main()
{
int i,item;
for(i=0;i<10;i++)
{
scanf("%d",&item);
insert1(item);
}
searchBST(root,100);
printf("\n");
searchBST(root,90);
printf("\n");
searchBST(root,80);
printf("\n");
searchBST(root,70);
return 0;
}
void searchBST(BTNodeptr p,int n)
{
BTNodeptr cur=p;
while(cur!=NULL)
{
if(n>cur->val)
{
printf("%d ",cur->val);
cur=cur->right;
}
else if(n<cur->val)
{
printf("%d ",cur->val);
cur=cur->left;
}
else
{
printf("%d ",cur->val);
break;
}
}
}
我们先用Insert函数创建了一个有10个结点的二叉树:
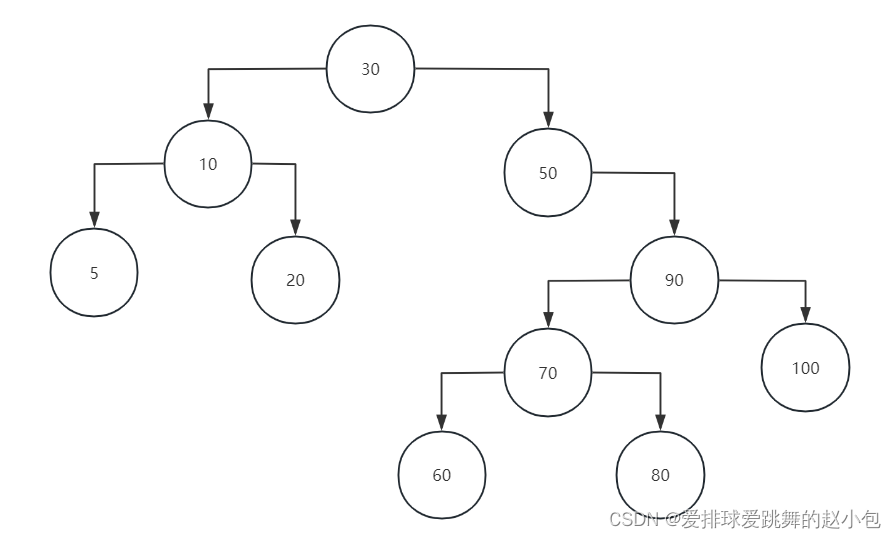 我们看看打印的祖先结点:
我们看看打印的祖先结点:

完全正确。
其实这个算法就是把刚刚的查找部分改了改。
在每一次判断大小的时候加了一个print语句。
普通二叉树:
这个时候也要用到遍历,但是只能是前序遍历。而且这时候要借助一个栈来存放祖先节点。
void preorder(BTNodeptr p,int item)
{
if(t!=NULL)
{
push(t);
if(item==t->data)
//弹出栈中所有元素
preorder(t->left);
preorder(t->right);
pop();
}
解释一下,就是我把一个子树的根结点放在了栈里,如果在这个子树的左子树里找到了目标,那么栈中所有元素就是路径;如果左子树里没有就转战右子树。如果两个子树都没找到,那说明这颗子树不行,“连根拔起”,也就是把刚刚放入栈中的子树根节点剔除栈。
搜索二叉树还有几个比较经典的题,比如:表达式树、词频统计,这个我们第五次作业里有,在下一篇文章中再整理。