一、经验总结
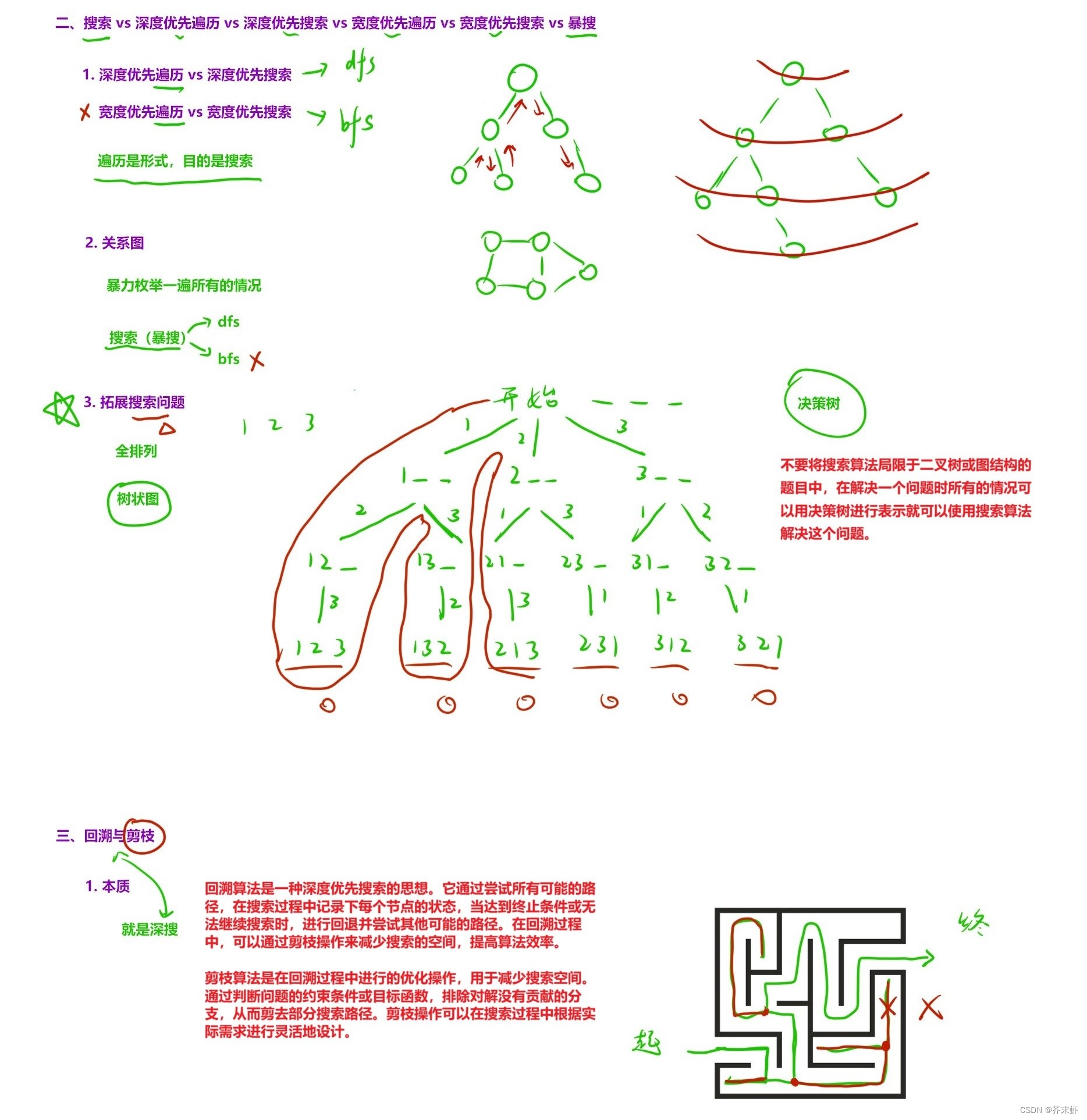
实际上递归、深度优先搜索(DFS)、回溯与剪枝研究的是同一类问题,我将其统称为递归深搜算法,其解题步骤大致如下:
-
画出递归决策树:如果遇到较为复杂的递归题目,可以通过画出决策树明晰递归流程,再抽象出递归的三个核心问题:函数头、函数体、递归出口。分析问题的角度不同,画出的决策树就可能不同,编写的递归函数也可能不同。
-
全局变量:在递归算法中常用到全局变量,全局变量的优势在于在递归和回溯的过程中保证每一层遍历访问的都是同一个变量。常用于收集结果、记录递归路径等。
-
回溯恢复现场:与全局变量的需求正好相反,在递归算法中某些变量需要在回溯到上一层递归后恢复现场。如果该变量为全局变量则需要在回溯到上一层后手动恢复;如果该变量为局部变量(局部参数),则每层递归的变量都是全新、独立的变量不会相互影响,在回溯过程中能够自动实现“恢复现场”。
-
剪枝优化:在回溯过程中,如果目前已经能够得出结论,则没有必要继续递归遍历其他分支,可以直接返回。排除对解没有贡献的分支,可以减少搜索空间。
二、相关编程题
2.1 计算布尔二叉树的值
题目链接
2331. 计算布尔二叉树的值 - 力扣(LeetCode)
题目描述
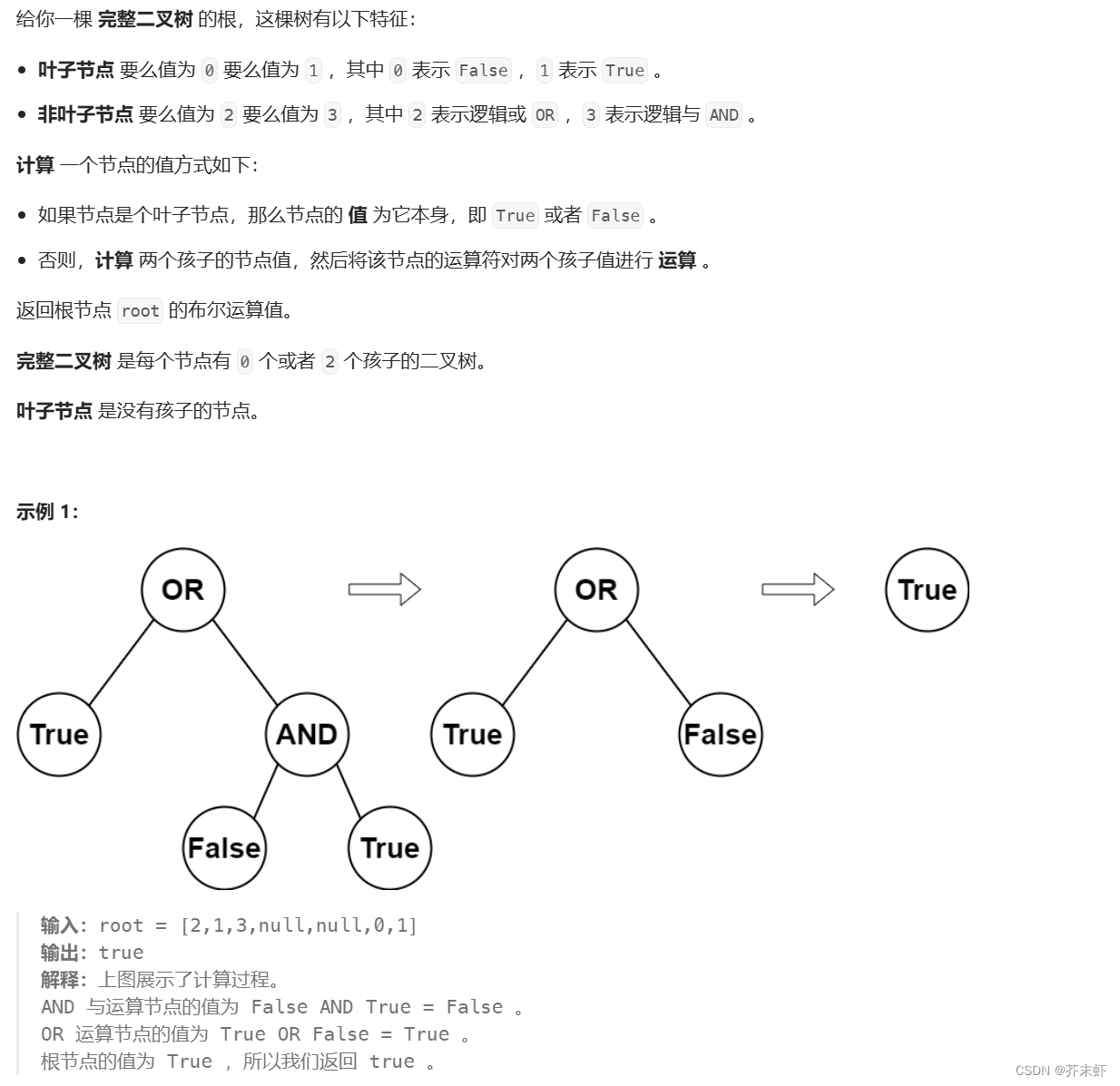
算法原理
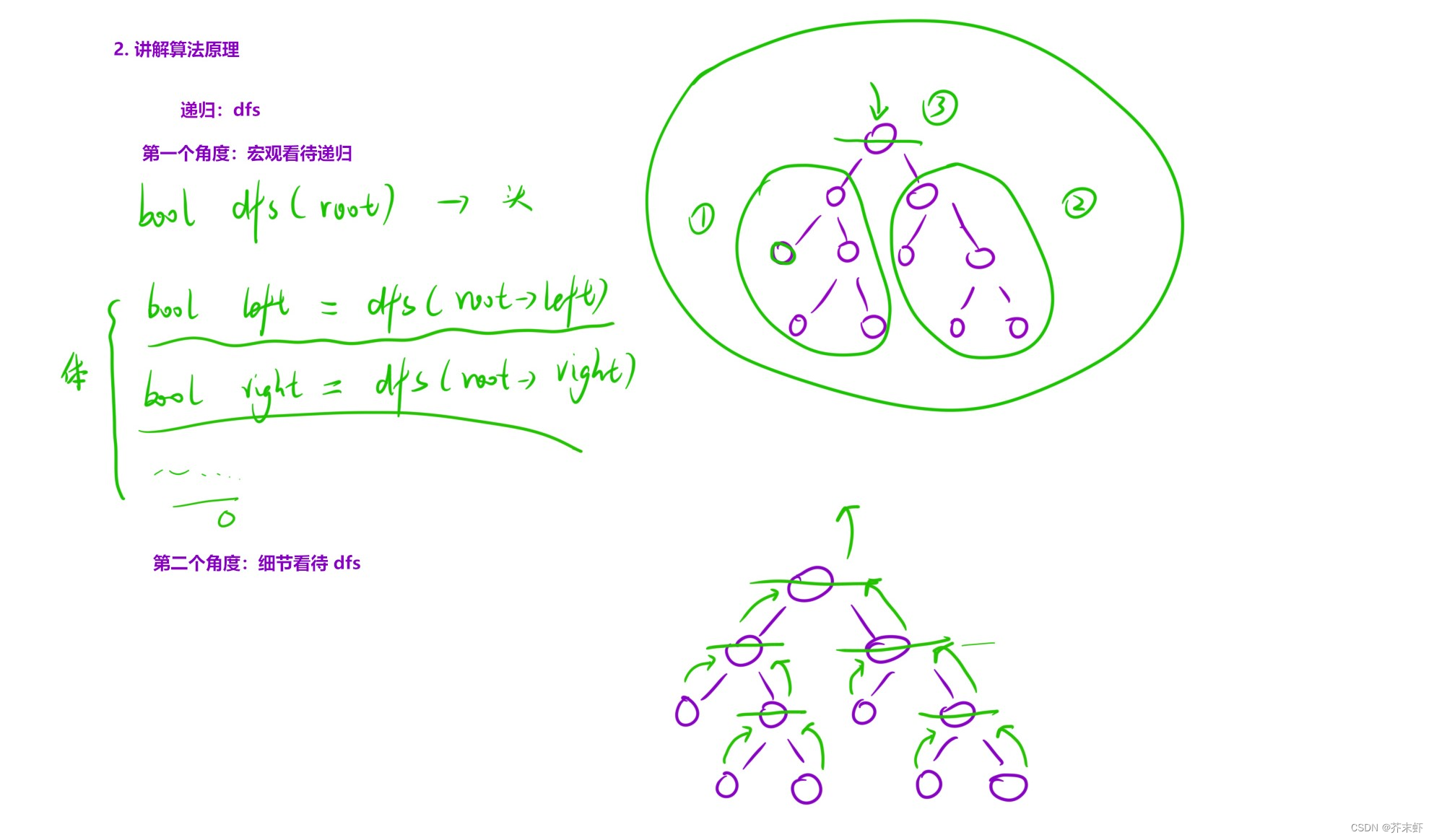
编写代码
class Solution {
public:
bool evaluateTree(TreeNode* root) {
if(root->val==0) return false;
if(root->val==1) return true;
bool bleft = evaluateTree(root->left);
bool bright = evaluateTree(root->right);
if(root->val==2) return bleft || bright;
else return bleft && bright;
}
};
2.2 求根节点到叶节点数字之和
题目链接
129. 求根节点到叶节点数字之和 - 力扣(LeetCode)
题目描述

算法原理
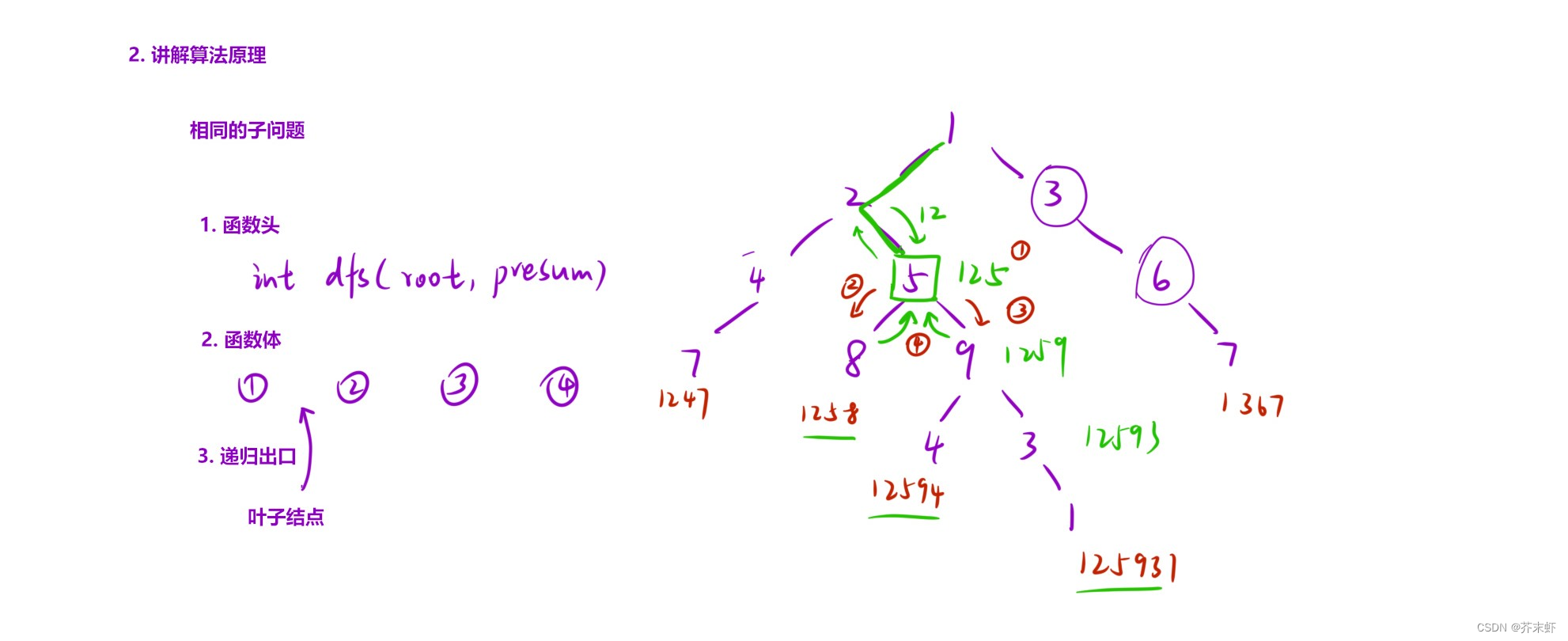
编写代码
class Solution {
public:
int sumNumbers(TreeNode* root) {
return DFS(root, 0);
}
int DFS(TreeNode* root, int prev)
{
prev = prev*10+root->val;
if(root->left==nullptr && root->right==nullptr)
return prev;
int ret = 0;
if(root->left!=nullptr)
ret += DFS(root->left, prev);
if(root->right!=nullptr)
ret += DFS(root->right, prev);
return ret;
}
};
2.3 二叉树剪枝
题目链接
814. 二叉树剪枝 - 力扣(LeetCode)
题目描述
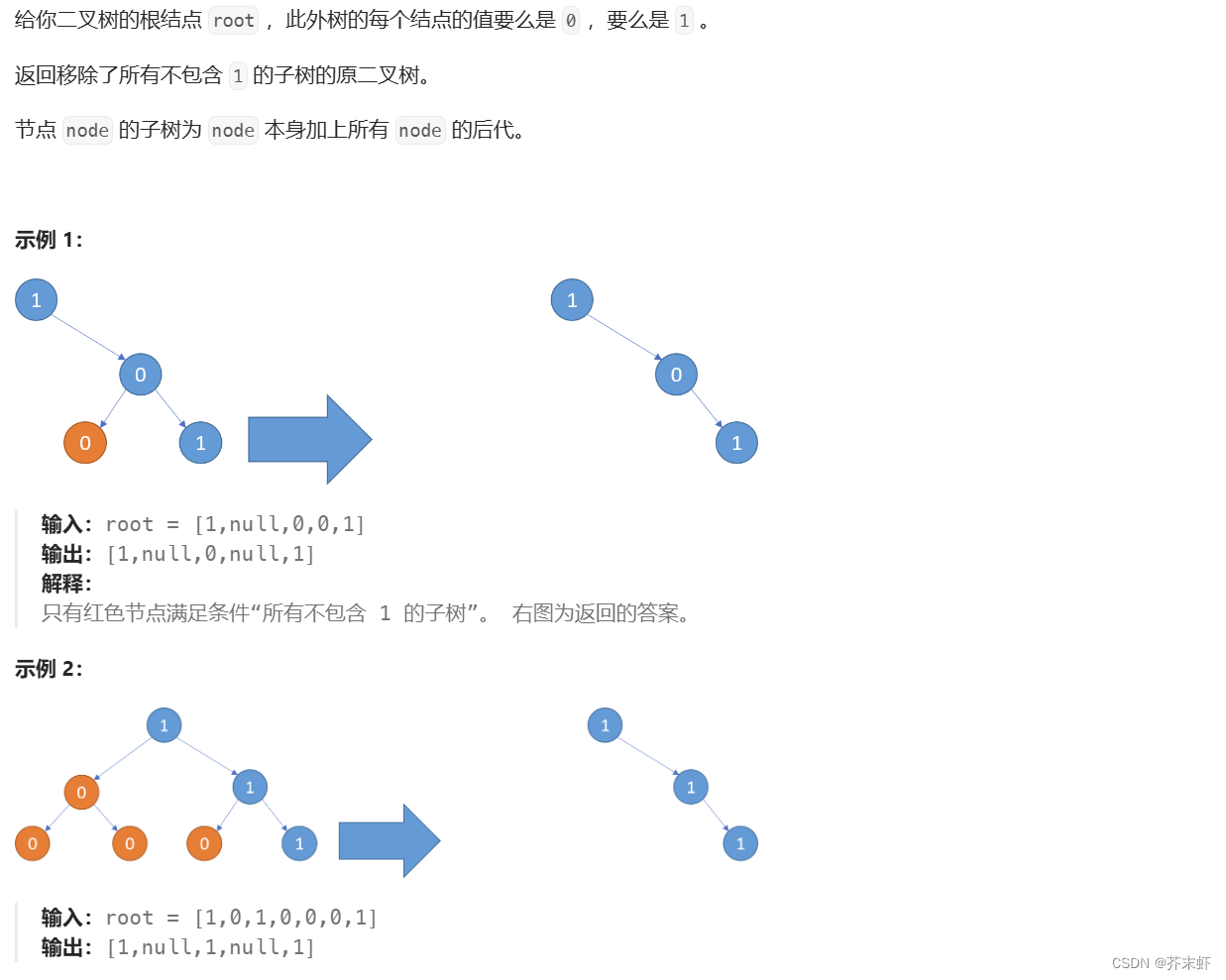
算法原理

编写代码
class Solution {
public:
TreeNode* pruneTree(TreeNode* root) {
if(root == nullptr) return nullptr;
root->left = pruneTree(root->left);
root->right = pruneTree(root->right);
if(root->left == nullptr && root->right == nullptr && root->val==0)
{
delete root;
return nullptr;
}
else
return root;
}
};
2.4 验证二叉搜索树
题目链接
98. 验证二叉搜索树 - 力扣(LeetCode)
题目描述
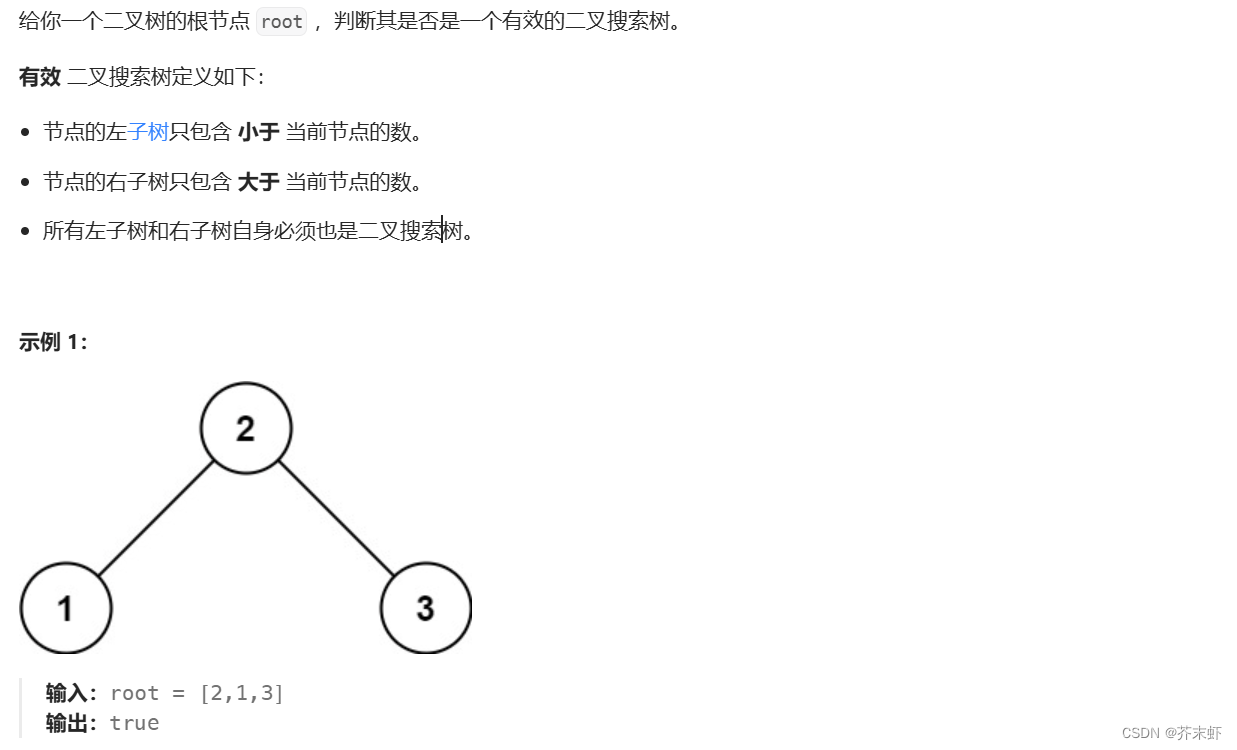
算法原理
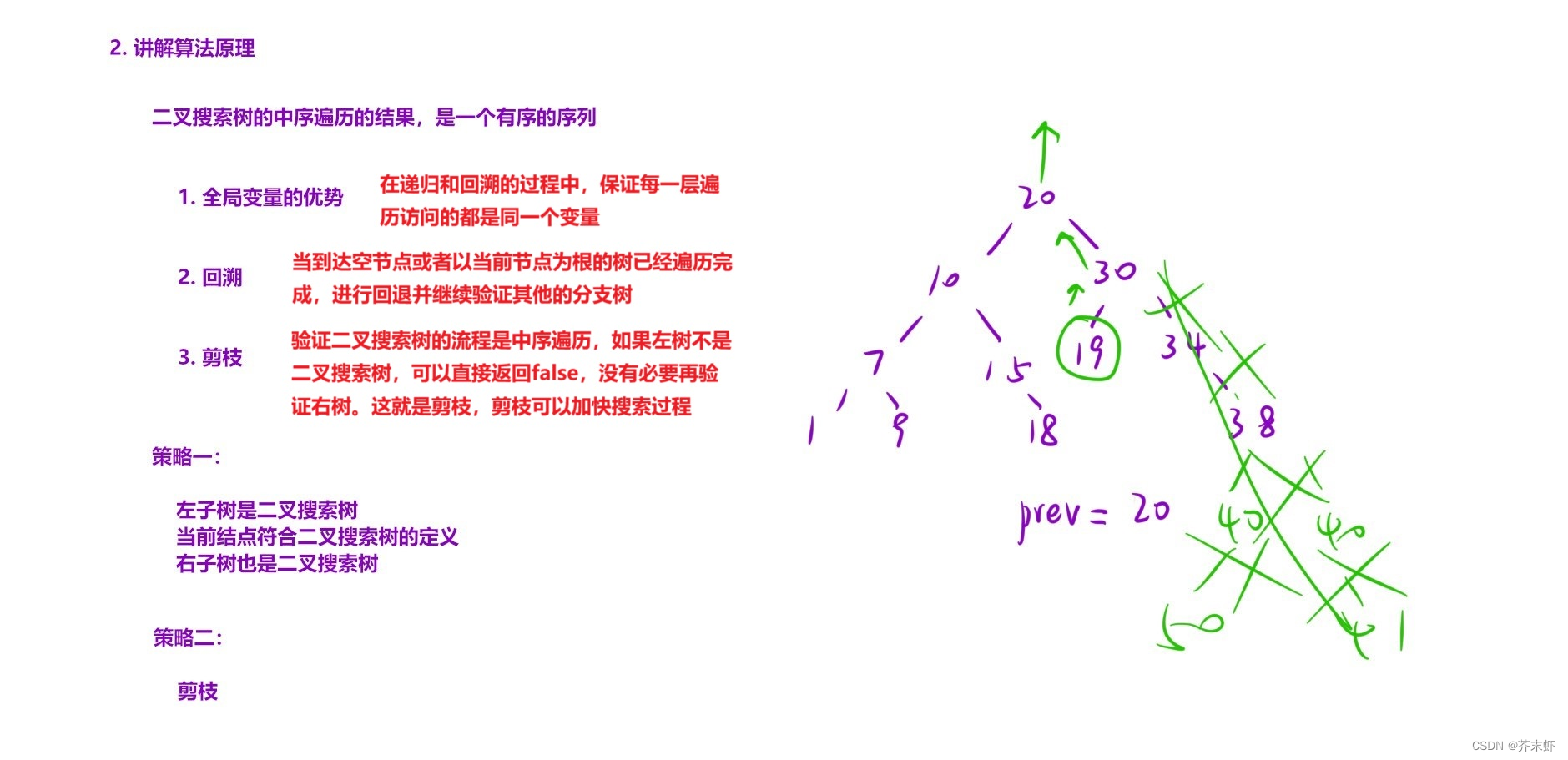
编写代码
class Solution {
long prev = LONG_MIN; //防止进行比较的第一个节点就是INT_MIN
public:
bool isValidBST(TreeNode* root) {
if(root == nullptr) return true;
if(!isValidBST(root->left)) //剪枝
return false;
if(root->val <= prev) //剪枝
return false;
prev = root->val;
if(!isValidBST(root->right))
return false;
return true;
}
};
2.5 二叉搜索树中第K小的元素
题目链接
230. 二叉搜索树中第K小的元素 - 力扣(LeetCode)
题目描述

算法原理
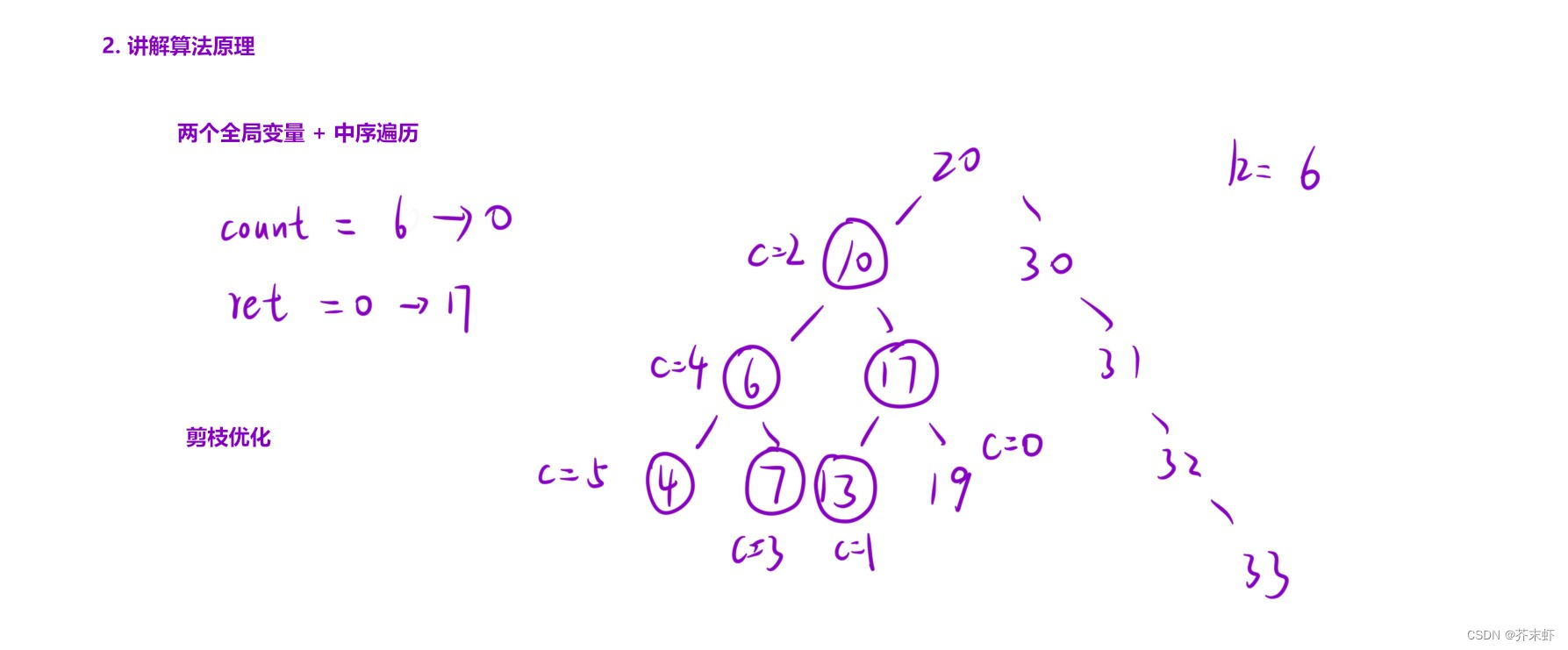
编写代码
class Solution {
int count, ret;
public:
int kthSmallest(TreeNode* root, int k) {
count = k;
DFS(root);
return ret;
}
void DFS(TreeNode* root)
{
if(root == nullptr) return;
if(count > 0) DFS(root->left);
if(count == 1) ret = root->val;
--count;
if(count > 0) DFS(root->right);
}
};
2.6 二叉树的所有路径
题目链接
257. 二叉树的所有路径 - 力扣(LeetCode)
题目描述
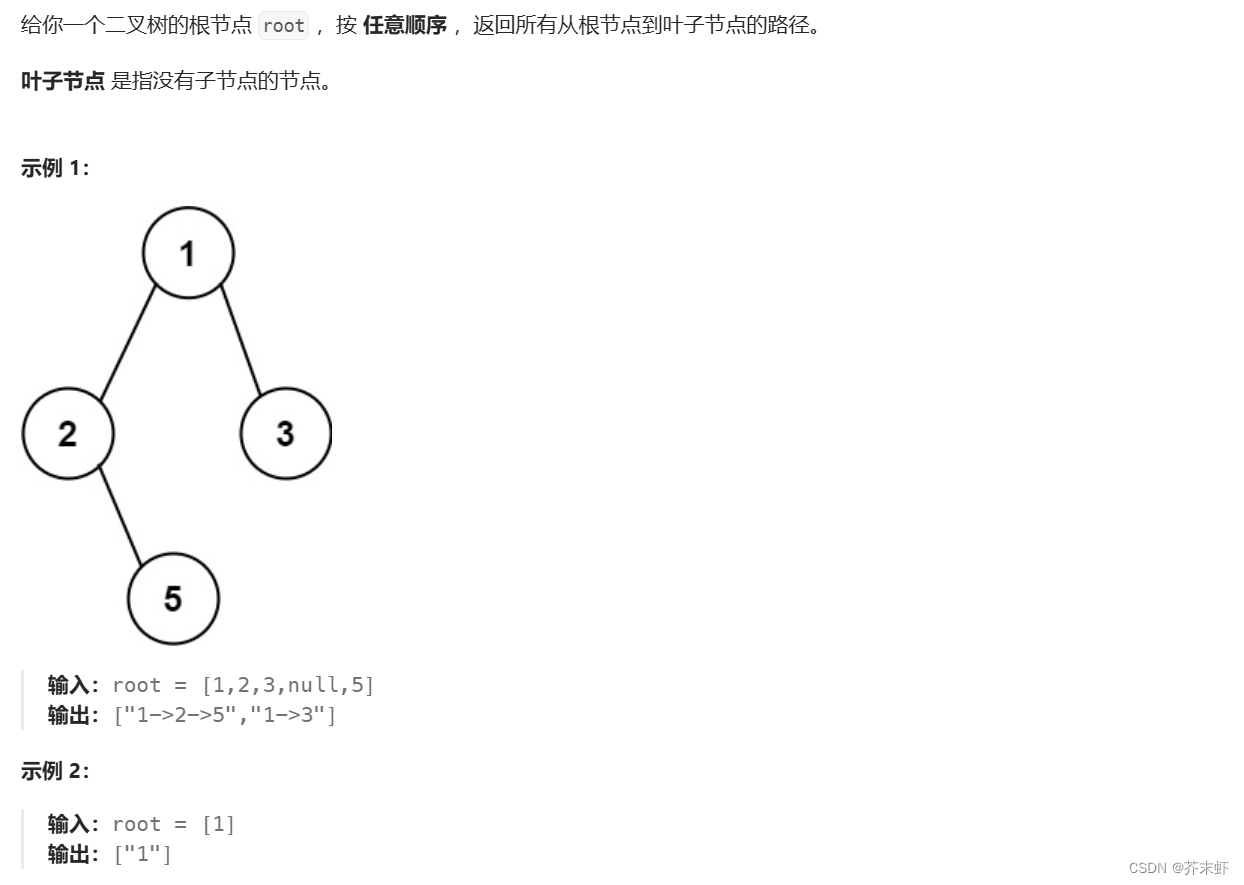
算法原理
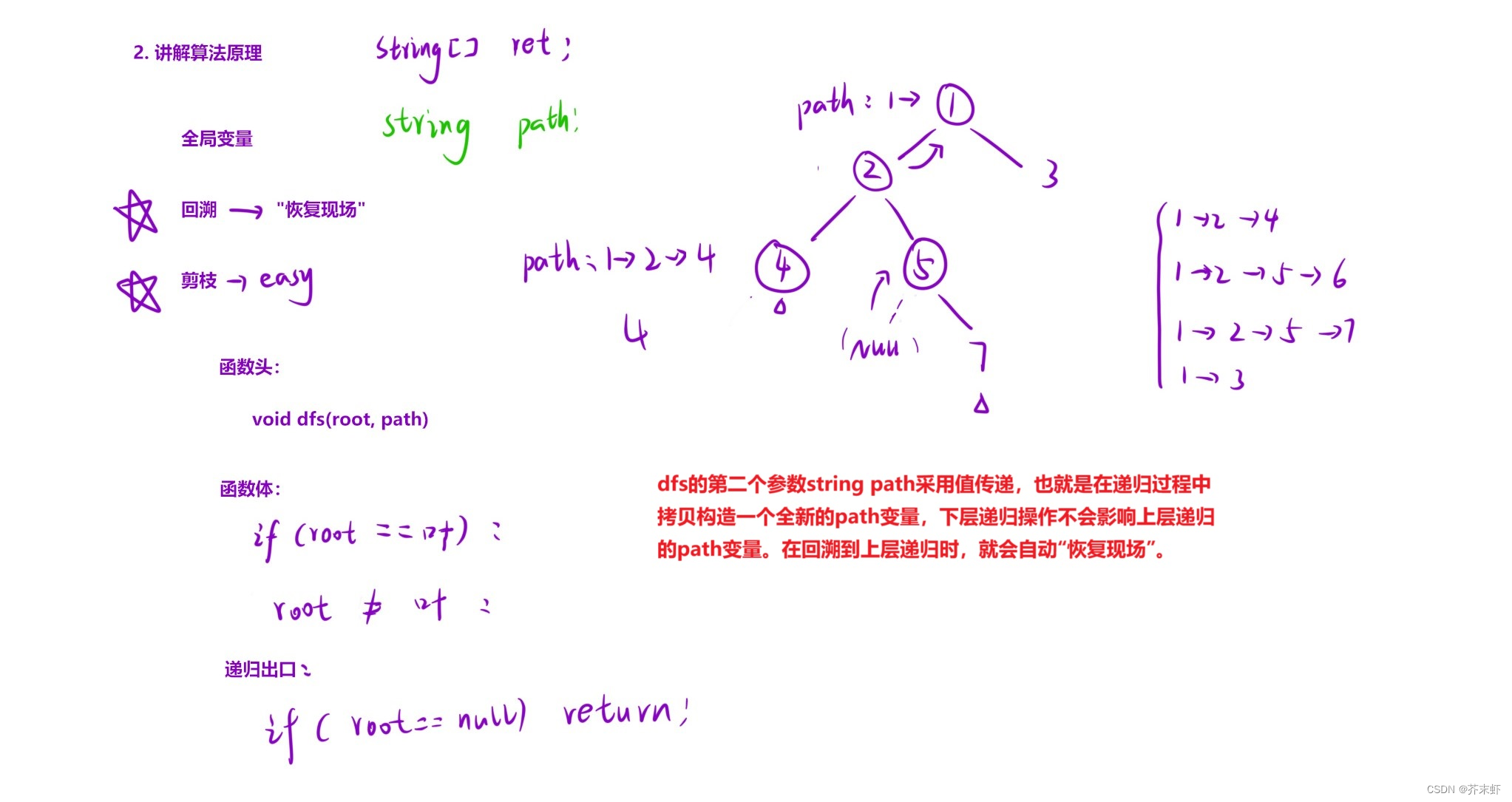
编写代码
class Solution {
vector<string> ret;
public:
vector<string> binaryTreePaths(TreeNode* root) {
DFS(root, "");
return ret;
}
void DFS(TreeNode* root, string str)
{
if(root == nullptr) return;
str+=to_string(root->val);
if(root->left==nullptr && root->right==nullptr)
{
ret.push_back(str);
return;
}
else
str+="->";
DFS(root->left, str);
DFS(root->right, str);
}
};
2.7 全排列
题目链接
46. 全排列 - 力扣(LeetCode)
题目描述

算法原理

编写代码
class Solution {
vector<vector<int>> ret;
vector<int> path;
bool used[6];
public:
vector<vector<int>> permute(vector<int>& nums) {
DFS(nums);
return ret;
}
void DFS(const vector<int>& nums)
{
if(path.size() == nums.size())
{
ret.push_back(path);
return;
}
for(int i = 0; i < nums.size(); ++i)
{
if(!used[i])
{
path.push_back(nums[i]);
used[i] = true;
DFS(nums);
//回溯恢复现场
path.pop_back();
used[i] = false;
}
}
}
};
2.8 子集
题目链接
78. 子集 - 力扣(LeetCode)
题目描述

算法原理
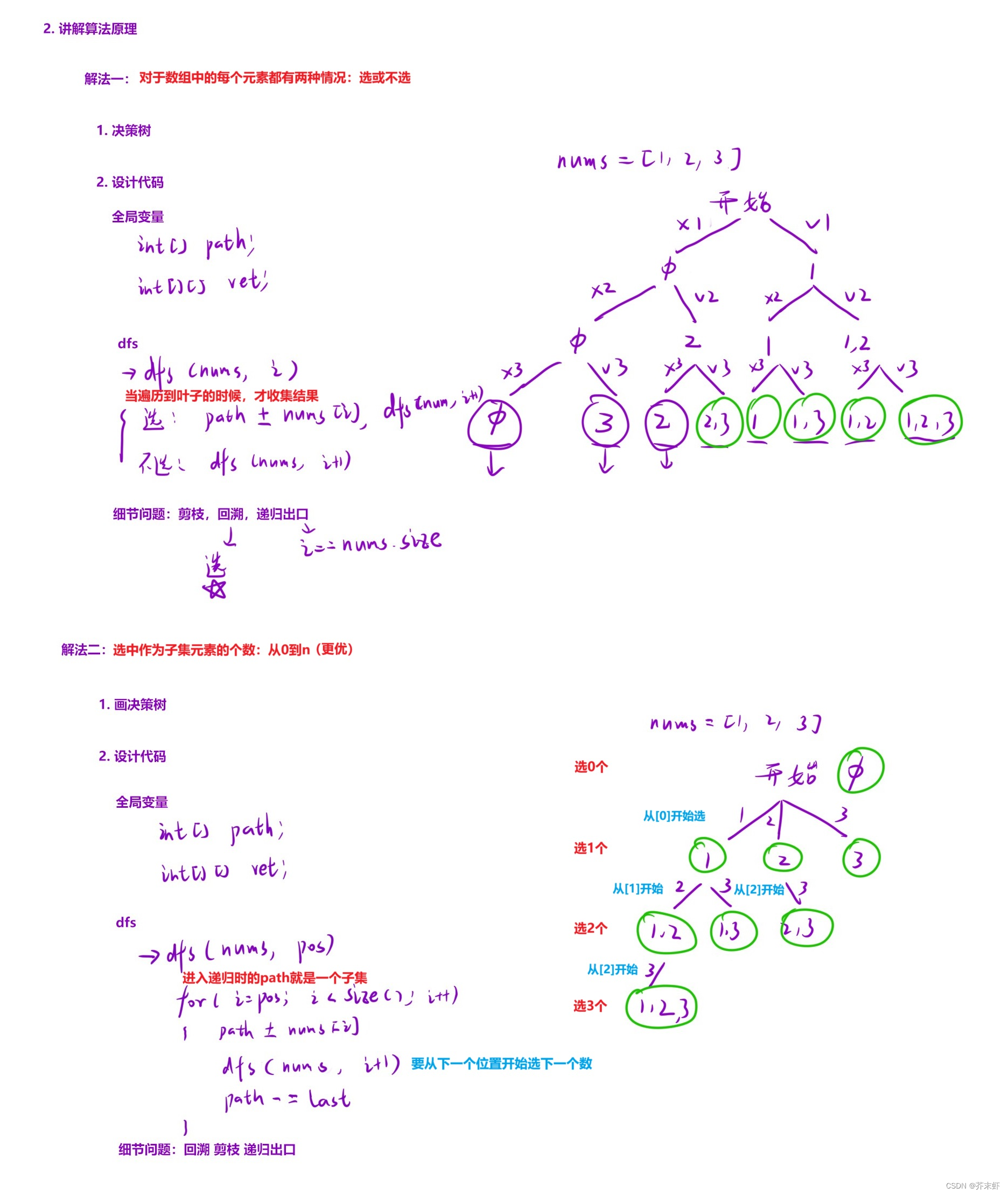
编写代码
class Solution {
vector<vector<int>> ret;
vector<int> path;
public:
vector<vector<int>> subsets(vector<int>& nums) {
DFS(nums, 0);
return ret;
}
//解法一:
void DFS(const vector<int>& nums, int i)
{
//当遍历到叶子时,才能返回结果
if(i == nums.size())
{
ret.push_back(path);
return;
}
//选
path.push_back(nums[i]);
DFS(nums, i+1);
path.pop_back(); //恢复现场
//不选
DFS(nums, i+1);
}
//解法二:
void DFS(vector<int>& nums, int pos)
{
ret.push_back(path); //进入递归时的path就是一个子集
for(int i = pos; i<nums.size(); ++i)
{
path.push_back(nums[i]);
DFS(nums,i+1); //要从下一个位置开始选下一个数
path.pop_back(); //恢复现场
}
}
};