文章目录
- 一、前言
- 二、问题
- 问题:1468. 小鱼的航程
- 问题:1074 - 小青蛙回来了
- 问题:1261. 韩信点兵
- 问题:1254. 求车速
- 问题:1265. 爱因斯坦的数学题
- 三、感谢
一、前言
本节主要对循环中需要流程控制的题目进行讲解,包括《1468. 小鱼的航程》《1074 - 小青蛙回来了》《1261. 韩信点兵》《1254. 求车速》《1265. 爱因斯坦的数学题》题目。
二、问题
问题:1468. 小鱼的航程
类型:需要找规律的循环
题目描述:
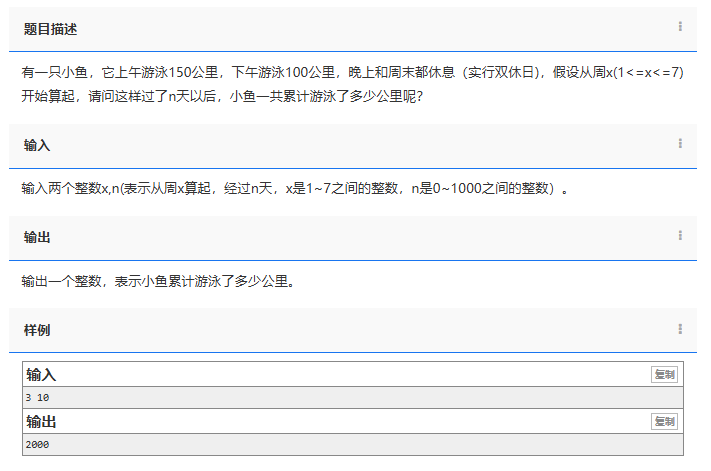
有一只小鱼,它上午游泳150公里,下午游泳100公里,晚上和周末都休息(实行双休日),假设从周x(1<=x<=7)开始算起,请问这样过了n天以后,小鱼一共累计游泳了多少公里呢?
输入:
输入两个整数x,n(表示从周x算起,经过n天,x是1~ 7之间的整数,n是0~1000之间的整数)。
输出:
输出一个整数,表示小鱼累计游泳了多少公里。
样例:
输入:
3 10
输出:
2000
1.分析问题
- 已知::从周x开始,经过n天。
- 未知:计算小鱼这n天里累计游泳了多少公里。
- 关系:上午游泳150公里,下午游泳100公里,晚上和周末都休息。
2.定义变量
- 分别定义了变量x(开始的周几),n(经过的天数),以及s(累计游泳的距离,初始为0)。
//二、数据定义
int x,n,s=0;
3.输入数据
- 从用户那里获取开始的周几(x)和经过的天数(n)。
//三、数据输入
cin>>x>>n;
4.数据计算
通过一个for循环,遍历从第1天到第n天。
- 对于每一天,首先检查是否为周六或周日(x等于6或7),如果是,则将日期递增并跳过当天(使用continue语句)。
- 如果不是周末,就累加每天游泳的总距离250公里(上午150公里加上下午100公里)到变量s中,并将日期x递增以模拟时间的推移。
//四、数据计算
for(int i=1;i<=n;i++){
if(x==6){
++x;
continue;
}
if(x==7){
x=1;
continue;
}
s+=250;
++x;
}
5.输出结果
- 输出小鱼累计游泳的总距离。
//五、输出结果
cout<<s;
完整代码如下:
#include<bits/stdc++.h> // 引入标准库,包含常用的数据结构和算法
using namespace std; // 使用std命名空间,简化对标准库中元素的调用
int main(){ // 程序的主入口函数
// 一、分析问题
// 给定小鱼从周x开始游泳,持续n天,需要计算这n天里小鱼总共游泳了多少公里。
// 小鱼的工作日(周一到周五)上午游泳150公里,下午游泳100公里;周末不游泳。
// 二、数据定义
int x,n,s=0; // x: 开始游泳的周几, n: 总共游泳的天数, s: 累计游泳的总距离(初始为0)
// 三、数据输入
cin>>x>>n; // 从用户处读取开始游泳的周几(x)和总天数(n)
// 四、数据计算
for(int i=1; i<=n; i++){ // 遍历从第一天到第n天
// 如果当前是周六或周日,则日期加1进入下一天(周末不游泳)
if(x==6){
++x;
continue; // 跳过本次循环的剩余部分,直接开始下一次循环
}
if(x==7){
x=1; // 周日过后回到周一
continue;
}
// 非周末,每天游泳总距离为250公里(上午+下午)
s += 250; // 累加到总距离s中
++x; // 日期递增,模拟到下一天
}
// 五、输出结果
cout<<s; // 输出小鱼累计游泳的总距离
return 0; // 主函数正常结束,返回0表示成功
}
问题:1074 - 小青蛙回来了
类型:需要找规律的循环
题目描述:
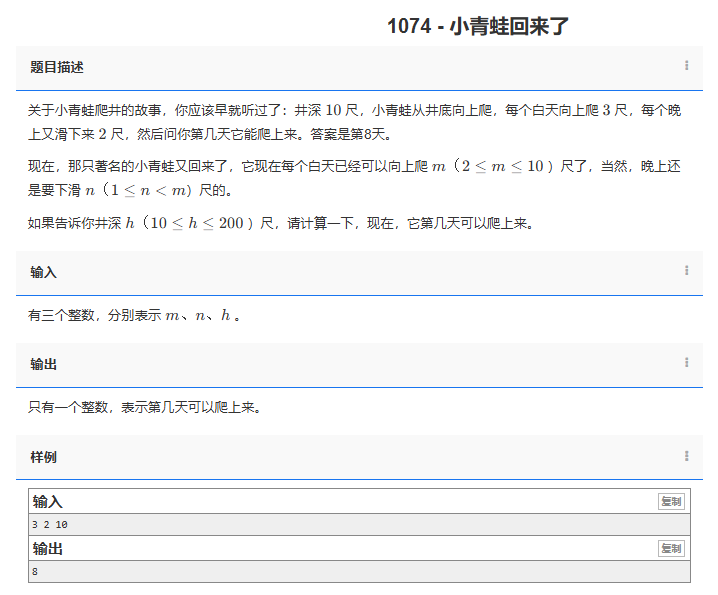
关于小青蛙爬井的故事,你应该早就听过了:井深10 尺,小青蛙从井底向上爬,每个白天向上爬 3 尺,每个晚上又滑下来 2 尺,然后问你第几天它能爬上来。答案是第8天。
现在,那只著名的小青蛙又回来了,它现在每个白天已经可以向上爬 m(2≤m≤10 )尺了,当然,晚上还是要下滑n(1≤n<m)尺的。
如果告诉你井深h(10≤h≤200 )尺,请计算一下,现在,它第几天可以爬上来。
输入:
有三个整数,分别表示 m、n、h 。
输出:
只有一个整数,表示第几天可以爬上来。
样例:
输入:
3 2 10
输出:
8
1.分析问题
- 已知:一只青蛙在白天可以向上爬m尺(2≤m≤10),但每到晚上会下滑n尺(1≤n<m)。井的深度为h尺(10≤h≤200)。
- 未知:确定青蛙需要多少天能从井底爬出来。
2.定义变量
- 定义变量 m、n 和 h 分别表示白天爬升高度、晚上下滑高度和井的深度;
- 定义 day=0 表示爬出井所花费的天数初值为0。
//二、数据定义
int m,n,h,day=0;
3.输入数据
- 从用户处获取白天爬升高度m、晚上下滑高度n以及井的深度h。
//三、数据输入
cin>>m>>n>>h;
4.数据计算
通过一个无限循环(while(true))来模拟每一天的过程,直到青蛙爬出井口。
- 每天开始时,青蛙先向上爬m尺,因此井的深度 h 减去 m。
- 判断如果井的深度 h 不足0(即青蛙已经爬出或正好在井口),则青蛙在下一天能完全爬出,因此将天数 day 加1后跳出循环。
- 若青蛙还未爬出,晚上它会下滑n尺,因此井的深度 h 再次加上 n,并且无论青蛙是否实际在井外,都算作度过了一整天,所以 day 自增1。
//四、数据计算
while(true){
h-=m;
if(h<=0){
++day;
break;
}
h+=n;
++day;
}
5.输出结果
//五、输出结果
cout<<day;
完整代码如下:
#include <bits/stdc++.h> // 包含标准库中的所有常用头文件,方便编程但可能影响编译速度
using namespace std; // 使用std命名空间,可以直接调用std下的函数和对象,无需std::前缀
int main() { // 程序的主函数
// 一、问题分析
// 青蛙每天白天爬上m尺,晚上滑下n尺,目标是从深度为h的井中爬出。
// 需要计算青蛙需要多少天才能完全爬出井。
// 二、数据定义
int m, n, h, day = 0; // m: 白天爬升高度, n: 晚上下滑高度, h: 井的深度, day: 青蛙爬出井所花的天数(初始化为0)
// 三、数据输入
cin >> m >> n >> h; // 从用户输入读取白天爬升高度m、晚上下滑高度n和井的深度h
// 四、数据计算
while (true) { // 无限循环,直到青蛙爬出井
h -= m; // 模拟青蛙白天爬上m尺
if (h <= 0) { // 检查青蛙是否达到或超过井口
++day; // 青蛙在这一天完全爬出,天数加1
break; // 结束循环,青蛙已成功爬出
}
h += n; // 若未达到,模拟晚上滑下n尺
++day; // 无论是进步还是退步,都算过完一天
}
// 五、输出结果
cout << day; // 输出青蛙爬出井所花的总天数
return 0; // 程序执行成功,返回0作为状态码
}
问题:1261. 韩信点兵
类型:
题目描述:
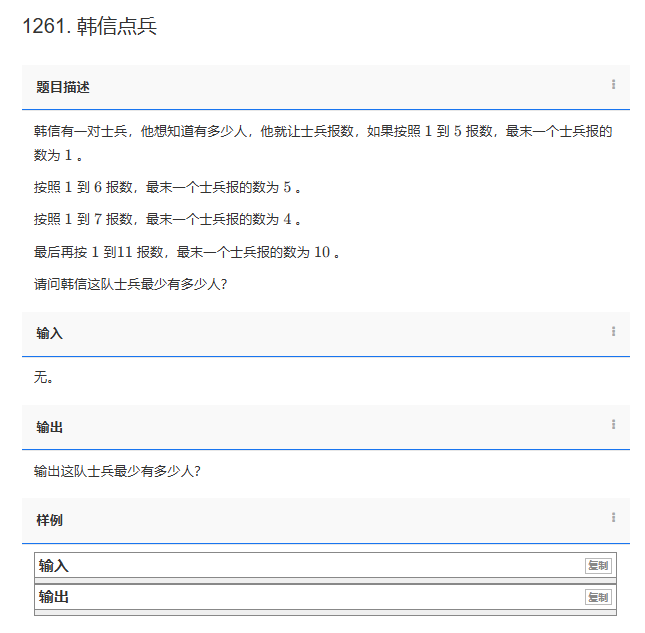
韩信有一对士兵,他想知道有多少人,他就让士兵报数,如果按照 1 到 5 报数,最末一个士兵报的数为 1 。
按照 1 到 6 报数,最末一个士兵报的数为 5 。
按照 1 到 7 报数,最末一个士兵报的数为 4 。
最后再按 1 到11 报数,最末一个士兵报的数为 10 。
请问韩信这队士兵最少有多少人?
输入:
无。
输出:
输出这队士兵最少有多少人?
1.分析问题
- 已知:
当报数周期为1至5时,队伍末尾士兵报的数是1。
当报数周期为1至6时,末尾士兵报的数是5。
当报数周期为1至7时,末尾士兵报的数是4。
当报数周期为1至11时,末尾士兵报的数是10。 - 未知:韩信这队士兵最少有多少人?
2.定义变量
- 初始化搜索的起始点,21是一个大于所有模数(5, 6, 7, 11)之和的数。
//二、数据定义
int p=21;
3.输入数据
无。
4.数据计算
无限循环:while(true) 用于持续检查直到找到解。
- 条件判断:if (p % 5 == 1 && p % 6 == 5 && p % 7 == 4 && p % 11 == 10) 检查当前数p是否满足所有报数条件。
- % 是取模运算符,用来计算除法的余数。
- 解的发现:一旦找到满足条件的p,使用break跳出循环。
- 递增搜索:若当前p不满足条件,则p++,尝试下一个数。
//四、数据计算
while(true){
if(p%5==1&&p%6==5&&p%7==4&&p%11==10){
break;
}
++p;
}
5.输出结果
- 输出找到的满足所有条件的最小士兵数。
//五、输出结果
cout<<p;
完整代码如下:
#include <bits/stdc++.h>
using namespace std;
int main() {
// 一、问题分析
// 已知报数规律:
// - 当报数周期为1至5时,最后一个士兵报数为1。
// - 当报数周期为1至6时,最后一个士兵报数为5。
// - 当报数周期为1至7时,最后一个士兵报数为4。
// - 当报数周期为1至11时,最后一个士兵报数为10。
// 未知:基于这些规律,韩信的部队至少有多少人?
// 二、数据定义
int p = 21; // 初始化搜索的最小人数为21,一个大于所有模数之和的初始猜测值
// 三、数据输入
// 此问题无需额外的数据输入,因为条件已经明确给出。
// 四、数据计算
while (true) {
// 使用循环检查当前猜测值p是否满足所有给定的报数条件
if (p % 5 == 1 && p % 6 == 5 && p % 7 == 4 && p % 11 == 10) {
// 当p同时满足所有条件时,退出循环
break;
}
++p; // 否则,将p加1继续测试下一个可能的士兵数
}
// 五、输出结果
cout << p; // 输出满足条件的最小士兵数
return 0; // 程序执行成功,返回0
}
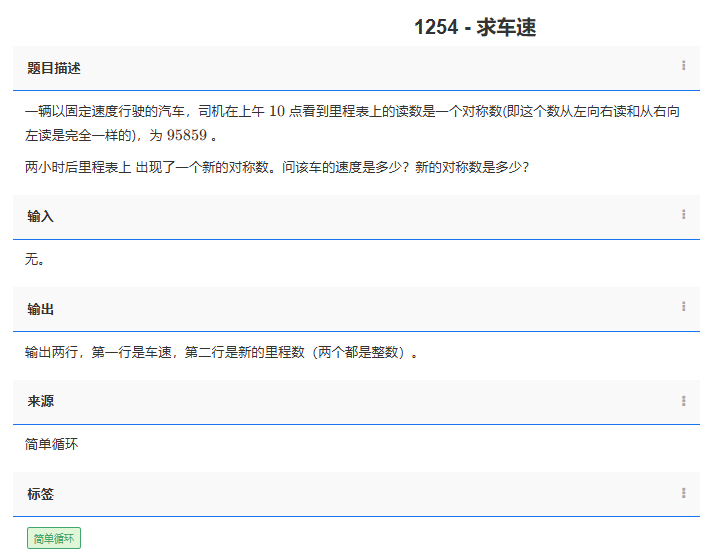
问题:1254. 求车速
类型:简单循环
题目描述:
一辆以固定速度行驶的汽车,司机在上午 10 点看到里程表上的读数是一个对称数(即这个数从左向右读和从右向左读是完全一样的),为95859 。
两小时后里程表上 出现了一个新的对称数。问该车的速度是多少?新的对称数是多少?
输入:
无。
输出:
输出两行,第一行是车速,第二行是新的里程数(两个都是整数)。
1.分析问题
- 已知:10 点里程表上的读数是一个对称数95859;
- 未知:该车的速度是多少?新的对称数是多少?
- 关系:两小时后里程表上 出现了一个新的对称数。
2.定义变量
- 首先定义了三个整型变量,os(old number,初始里程表读数)设为95859,p(行驶的速度)和ns(new number,新的对称数)。
//二、数据定义
int os=95859,p,ns;
3.输入数据
无。
4.数据计算
-
从初始里程数os+1开始,通过一个无限循环查找下一个对称数:
-
使用while(true)创建一个持续运行的循环,直到找到满足条件的对称数后通过break跳出。
- 判断条件为当前数的万位与个位相同,千位与十位相同,这是对称数的定义。
- 若当前数不符合对称条件,则ns递增,继续检查下一个数。
- 计算p的值,即(ns-os)/2。
//四、数据计算
ns=os+1;
while(true){
if((ns/10000==ns%10)&&(ns/1000%10==ns/10%10)){
break;
}
++ns;
}
p=(ns-os)/2;
5.输出结果
- 先输出p,为两小时内车辆行驶的平均速度。
- 再输出ns,即找到的新的对称数里程表读数。
//五、输出结果
cout<<p<<endl<<ns;
完整代码如下:
#include <bits/stdc++.h> // 包含标准库中的常用头文件
using namespace std; // 允许直接使用std命名空间中的函数和对象
int main() {
// 一、问题概述
// 已知10点时车辆里程表显示为一个对称数95859,
// 本程序旨在找出两小时后车辆达到的新对称数及这段时间的平均速度。
// 二、数据初始化
int os = 95859, // 初始里程表读数
p, // 两小时内的平均速度(将计算得出,单位取决于里程表读数单位与时间单位的比值)
ns; // 达到的新对称数里程表读数
// 三、寻找新对称数
// 从初始里程数加1开始,迭代查找下一个对称数
ns = os + 1;
while (true) {
// 判断当前数是否为对称数:首位与末位匹配,次位与倒数第二位匹配
if ((ns / 10000 == ns % 10) &&
(ns / 1000 % 10 == ns / 10 % 10)) {
break; // 找到新对称数,退出循环
}
++ns; // 当前数不对称,检查下一个
}
// 四、计算平均速度
// 两小时内行驶的总里程除以时间(2小时),得到平均速度
p = (ns - os) / 2;
// 五、输出结果
// 输出两小时内车辆的平均速度(基于里程变化估算)
cout << p << endl;
// 输出新的对称数里程表读数
cout << ns;
return 0; // 程序结束,返回0表示成功
}
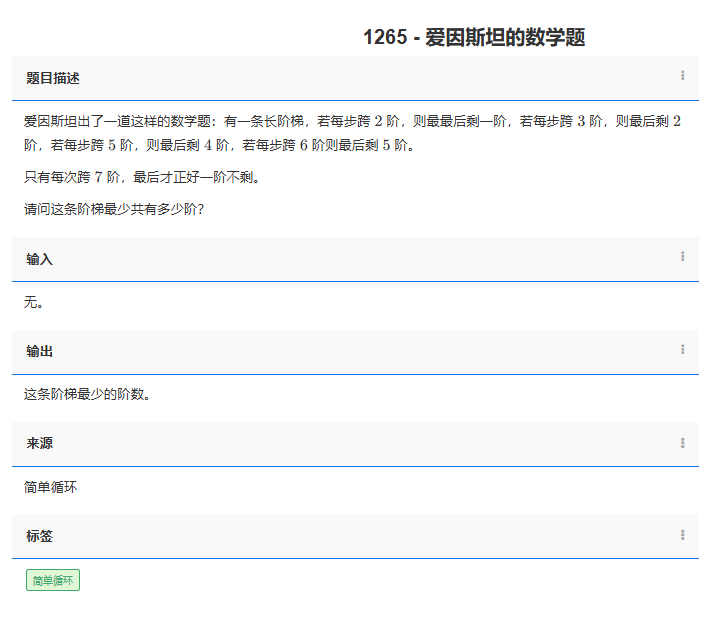
问题:1265. 爱因斯坦的数学题
类型:简单循环
题目描述:
爱因斯坦出了一道这样的数学题:有一条长阶梯,若每步跨 2 阶,则最最后剩一阶,若每步跨 3 阶,则最后剩 2 阶,若每步跨 5 阶,则最后剩 4 阶,若每步跨 6 阶则最后剩 5 阶。
只有每次跨 7 阶,最后才正好一阶不剩。
请问这条阶梯最少共有多少阶?
输入:
无。
输出:
这条阶梯最少的阶数。
1.分析问题
- 已知:有一条不知道阶梯数长阶梯;
- 未知:这条阶梯最少共有多少阶?
- 关系:若每步跨2阶,则最最后剩一阶,若每步跨3阶,则最后剩2阶,若每步跨5阶,则最后剩4阶,若每步跨6阶则最后剩5阶,只有每次跨7阶,最后才正好一阶不剩。
2.定义变量
- 初始化变量t为7,这是搜索满足条件的最小正整数的起始点。
//二、数据定义
int t=7;
3.输入数据
无。
4.数据计算
定义一个无限循环,直到找到满足所有给定条件的t值时通过break语句退出循环。
- if语句检查t是否同时满足所有模运算条件。
- 若当前t不满足条件,则t值通过t+=7;每次增加7,这是因为题目暗示只有跨7阶时,最后才能正好一阶不剩,意味着解的形式可能在一个以7为步长的序列中。
//四、数据计算
// 循环查找满足条件的最小阶梯数
while (true) {
// 检查当前阶梯数t是否满足所有给定的余数条件
if (t % 2 == 1 && t % 3 == 2 && t % 5 == 4 && t % 6 == 5) {
// 如果满足条件,跳出循环
break;
}
// 不满足条件,则按照每次跨7阶的规则增加阶梯数
t += 7;
}
5.输出结果
- 循环结束后,输出找到的满足条件的最小阶梯数t。
//五、输出结果
cout <<t;
完整代码如下:
#include <bits/stdc++.h>
using namespace std;
int main() {
//一、分析问题
//已知:有一条不知道阶梯数长阶梯
//未知:这条阶梯最少共有多少阶?
//关系:若每步跨2阶,则最最后剩一阶,若每步跨3阶,则最后剩2阶,若每步跨5阶,则最后剩4阶,若每步跨6阶则最后剩5阶,只有每次跨7阶,最后才正好一阶不剩。
//二、数据定义
int t=7;
//三、数据输入
//四、数据计算
// 循环查找满足条件的最小阶梯数
while (true) {
// 检查当前阶梯数t是否满足所有给定的余数条件
if (t % 2 == 1 && t % 3 == 2 && t % 5 == 4 && t % 6 == 5) {
// 如果满足条件,跳出循环
break;
}
// 不满足条件,则按照每次跨7阶的规则增加阶梯数
t += 7;
}
//五、输出结果
cout <<t;
return 0;
}
三、感谢
如若本文对您的学习或工作有所启发和帮助,恳请您给予宝贵的支持——轻轻一点,为文章点赞;若觉得内容值得分享给更多朋友,欢迎转发扩散;若认为此篇内容具有长期参考价值,敬请收藏以便随时查阅。
每一次您的点赞、分享与收藏,都是对我持续创作和分享的热情鼓励,也是推动我不断提供更多高质量内容的动力源泉。期待我们在下一篇文章中再次相遇,共同攀登知识的高峰!