0x0. 前言
在openreview上看到最近NV的一个KV Cache压缩工作:https://openreview.net/pdf?id=tDRYrAkOB7 ,感觉思路还是有一些意思的,所以这里就分享一下。
简单来说就是paper提出通过一种特殊的方式continue train一下原始的大模型,可以把模型在generate过程中的KV Cache分成多个段,并且每个token都会学出来一个0或者1的标记,对于标记为1的token的KV Cache可以累加到上一个标记为1的token的KV Cache上(需要这两个token连续才可以累加),而不是concat,这样就可以高效压缩KV Cache,效果也是不错的,且可以配合GQA联合使用。此外,它在continue train或者推理prefill的时候仍然可以用上Flash Attention,推理的decode阶段可以用上Paged Attention。
但是读完方法部分发现这个方法也有几个缺陷,估计会失去工程应用的机会,只能当一篇paper读一下。第一点就是要对整个模型做全量参数的continue train,虽然训练的数据可以很少,但是能把大模型加载起来的成本已经非常高了,普通人肯定这一步就卡死了。第二,这种方法不能from scratch训练,这样就更阻碍了这种方法的广泛应用,毕竟MLA的成功一个重要原因就是因为Deepseek2直接用这个架构from scratch训出来的model并开源。另外,这里的开源链接目前是空的,还不能看到代码细节。
0x1. 摘要
Transformer 已经成为大型语言模型 (LLM) 的核心。然而,由于需要在内存中存储过去token的key value的缓存(KV Cache),而缓存的大小与输入序列长度和batch大小线性相关,因此生成仍然效率低下。为了解决这个问题,paper提出了动态内存压缩 (DMC),一种在推理时对KV Cache进行在线压缩的方法。最重要的是,模型学习在不同的注意力头和layer中应用不同的压缩率。paper将预训练的 LLM(如 Llama 2(7B、13B 和 70B))改造为 DMC Transformer,在 NVIDIA H100 GPU 上进行自回归推理时,实现了高达 ~3.7 倍的吞吐量提升。DMC 通过在原始数据的极小百分比上进行continue pretrained来应用,而无需添加任何额外的参数。paper发现,DMC 在高达 4 倍的缓存压缩的情况下,保留了原始的下游性能,优于经过微调的分组查询注意力 (GQA) 和key value驱逐策略 (H2O、TOVA)。GQA 和 DMC 可以结合起来获得复合收益。因此,DMC 在任何给定的内存预算内都适合更长的上下文和更大的batch。我们在 https://github.com/NVIDIA/Megatron-LM/tree/DMC 上发布了 DMC 代码和模型。
0x2. 介绍
首先还是提到了大模型推理的时候KV Cache会伴随着序列长度和Batch大小不断增长,这个问题在长文本生成(例如,对话和故事)或为大量用户查询提供服务时更加明显。然后为了缓解这个问题,GQA,Key-Value驱逐策略比如H20,TOVA等被提出,然后Paper说这些方法往往会牺牲预训练模型的精度。另外Flash-Attention等IO-aware或者子平方注意力算法等都无法改善KV Cache。
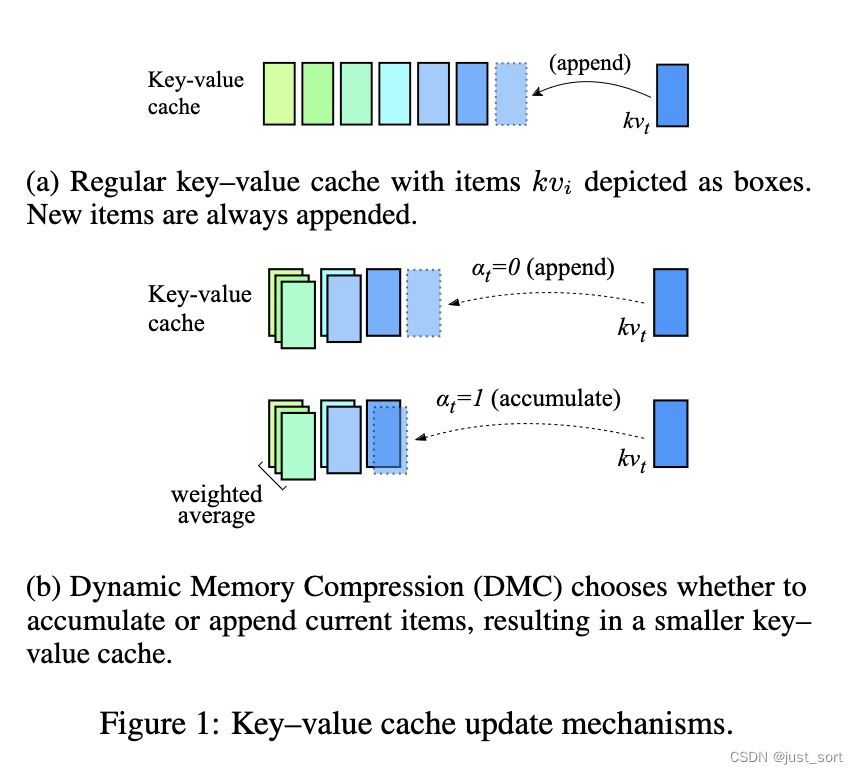
因此paper提出了动态内存压缩(DMC)方法对KV Cache进行压缩,如图 1 所示,在每个时间步长,DMC 会决定是将当前的key-value表示添加到缓存中,还是对它们与缓存中顶部的项进行加权平均。DMC 中的内存以亚线性方式增长,虽然比不上Linear Attention Transformer推理时的内存恒定,但明显好于Transformer。
作者团队使用了部分预训练数据(2%对应2倍压缩,4%对应4倍压缩)对应用了DMC的LLama 2(7B,13B)模型进行continue training。 paper在一些下游任务上评估了我们的 DMC 模型,例如 MMLU 用于事实性,QA 数据集用于常识推理,以及 HumanEval 用于代码。作者发现,DMC LLM 保持了与原始 LLM 相似的下游性能,而基线(如 GQA、H2O 和 TOVA)在高压缩率下会造成显著的性能下降。最后,作者表明 DMC 可以与 GQA 混合,使得它们的压缩率相乘。对于使用 GQA 8 倍预训练的 Llama 2 70B,DMC 2 倍可以实现总共 16 倍的压缩。
作者验证了 KV 缓存压缩在实践中可以转化为更有效的生成。 最后测量到,DMC 4 倍在不损失性能的情况下,将 Llama 2 7B 和 13B 在 NVIDIA H100 或 A100 GPU 上的推理吞吐量提高了 340% 到 370%。事实上,它使大模型能够在给定的内存预算中容纳更大的batch和更长的序列。
0x3. 动态内存压缩方法(DMC)
LLM 的推理通常受内存限制,而不是计算能力限制。减少 KV Cache的大小可以降低延迟并提高 GPU 利用率。DMC 是一种简单且廉价的在线压缩 KV Cache的方法。通过continue pretrain,可以教会预训练的 LLM 使用 DMC。
0x3.1 推理
考虑自回归推理过程中注意力层的正向传播。 在普通 Transformer 中,在每个时间步 t t t, k t k_t kt 和 v t v_t vt 都会被追加到 KV Cache中。另一方面,在 DMC 中,KV Cache更新过程有所不同,如算法 1 所示。首先,预测一个决策变量 α t ∈ \alpha_t \in αt∈ {0, 1} (只能取0和1) 和一个重要性变量 ω t ∈ [ 0 , 1 ] ω_t ∈ [0, 1] ωt∈[0,1]。为了避免添加新的参数,我们分别重用 k t k_t kt 和 q t q_t qt 中的第一个神经元来提取这两个分数。根据 α t \alpha_t αt,决定是将 KV 表示 k t k_t kt 和 v t v_t vt 追加到缓存中,还是将其与缓存的最后一个元素累加。

具体来说,对于累加,paper根据对当前token预测的重要性分数 ω ω ω 和自上次预测 α = 0 \alpha = 0 α=0 以来所有 token 的重要性分数之和 z t z_t zt 进行加权平均。 事实上, α \alpha α变量有效地将输入序列分割:每个决策决定当前段是否应该继续( α = 1 \alpha = 1 α=1)或是否应该打开一个新段( α = 0 \alpha = 0 α=0)。更新后,DMC 的缓存长度为 l = ∑ t = 1 n ( 1 − α t ) < = n l = \sum_{t=1}^{n}(1-\alpha_t)<=n l=∑t=1n(1−αt)<=n,而在普通 Transformer 中,它始终为 l = n l = n l=n。在下文中,将未压缩缓存的长度 n n n 与压缩长度 l l l 之间的比率 n / l n/l n/l 称为压缩率 (CR)。最后,多头自注意力与普通 Transformer 的计算方式类似,使用 KV Cache序列,区别在于不同头的 KV 序列可能具有不同的长度。 算法 1 对每个 MHSA 层和头独立地应用。请注意,算法 1 可以有效地实现,无需根据 α t \alpha_t αt 进行 if-then-else 语句,而是像公式(9)中那样将之前的 k i k_i ki、 v i v_i vi 和 z i z_i zi 乘以 α t \alpha_t αt。
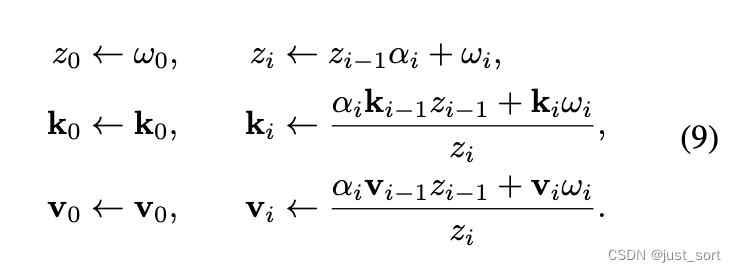
0x3.2 训练
DMC 推断算法在累积和追加token到 KV Cache之间切换。为了赋予 LLM DMC 功能,我们在少量预训练数据上继续对它们进行预训练,逐渐提高压缩率以达到目标。然而,这带来了严峻的挑战。首先,我们选择通过梯度下降和决策变量的连续松弛来进行端到端学习。因此,我们必须定义一个 KV 缓存更新操作,当 0 < α < 1 0 < \alpha < 1 0<α<1 时,导致部分聚合、部分累积的key和value状态。其次,为了避免训练-推断不匹配,我们必须在推断时模拟 DMC 行为,同时跨一系列tokens 并行训练:因此, K K K 和 V V V 的长度在训练期间不会通过压缩减少;相反,keys 和 values 的中间状态都显式地保存在内存中,并且一个辅助的(逐渐离散化的)掩码调节 query 和 key 之间的交互。
离散决策的梯度估计
推理时是累积还是追加的决策是离散的;然而,在训练中将
s
i
g
m
o
i
d
(
k
[
0
]
)
sigmoid(k[0])
sigmoid(k[0])四舍五入到最接近的整数会导致非可微分操作,梯度为零。因此,我们在训练过程中采用决策变量的随机重参数化。
α t ∼ Gumbel-sigmoid ( k [ 0 ] − c , τ ) ∈ [ 0 , 1 ] , \alpha_t \sim \text{Gumbel-sigmoid}(k[0] - c, \tau) \in [0, 1], αt∼Gumbel-sigmoid(k[0]−c,τ)∈[0,1],
其中, τ \tau τ 是温度( 低温度将 α t 锐化为几乎离散的值,这准确地模仿了推理行为。 低温度将\alpha_t 锐化为几乎离散的值,这准确地模仿了推理行为。 低温度将αt锐化为几乎离散的值,这准确地模仿了推理行为。), c c c 是一个常数,减去它是为了使在训练步骤0时,每个 α ≈ 0 \alpha≈0 α≈0。同样地,我们将 c c c加到重要性变量 ω t ω_t ωt中,以便在开始时每个 ω t ≈ 1 ω_t≈1 ωt≈1。这确保了DMC最初不执行压缩,且训练表现如同普通的Transformer。
部分累积
随着我们放宽离散决策,我们现在必须定义一个机制来更新KV缓存,使其将算法1推广到连续的
α
\alpha
α。因此,我们定义部分累积状态对于
α
∈
[
0
,
1
]
α \in [0, 1]
α∈[0,1]如下:
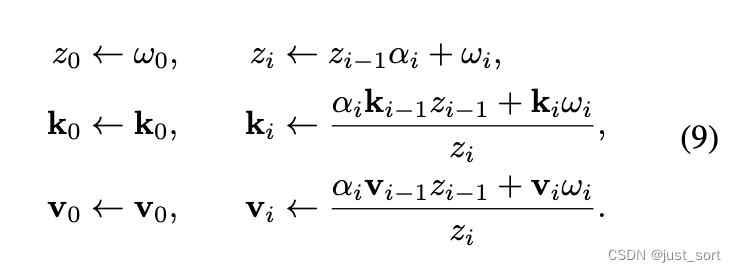
注意,当 α \alpha α ∈ {0, 1}时,方程(9)会退化为算法1。
中间压缩步骤
除了方程(9)中显示的key和value的计算,Forward Pass其余部分可以对序列中的所有tokens并行执行。然而,这在训练和评估之间造成了不匹配,因为在训练期间,所有key和value的中间状态在自注意力机制中都是可访问的。
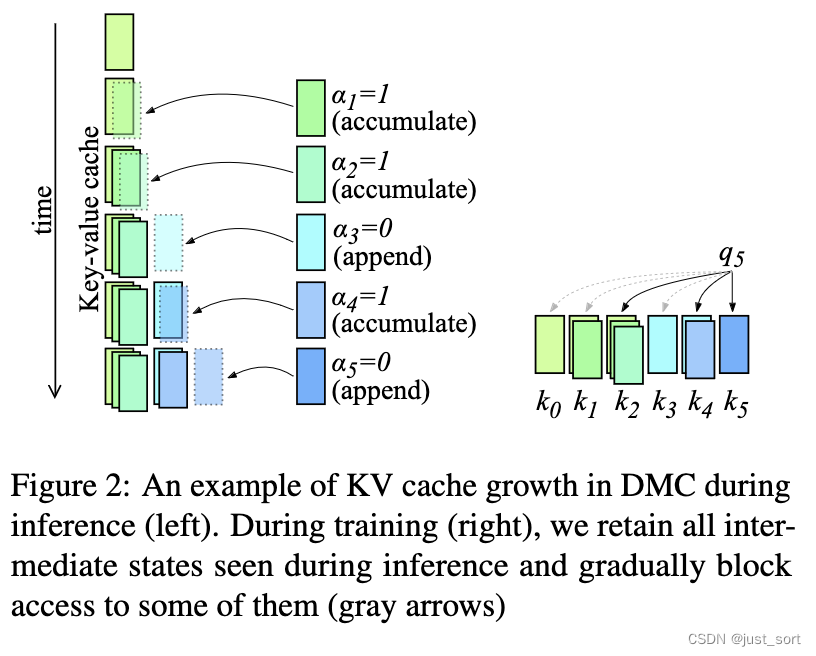
为了说明这个问题,请考虑上图2中DMC推理期间的KV Cache示例,决策分数序列为 α 1 : 5 = ( 1 , 1 , 0 , 1 , 0 ) \alpha_{1:5} = (1, 1, 0, 1, 0) α1:5=(1,1,0,1,0)(为简明起见,已省略重要性分数 ω \omega ω)。KV Cache的最后一个元素在每个时间步都会发生变化。为了在训练期间正确模拟推理时间KV Cache的演变,保留所有展开的中间KV Cache项。

论文使用基于 α \alpha α值序列的加性掩码来修改方程(4)中的注意力分数 a i j h a^h_{ij} aijh,如上图3所示。
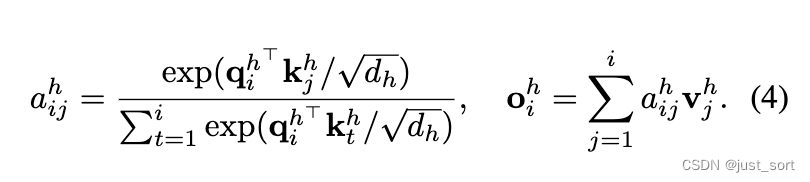
在训练期间, α \alpha α值 1) 自然地收敛到0或1,因为模型努力满足语言建模标准并减少不确定性;2)通过Gumbel噪声和低温设置被故意推向几乎离散的状态。这样的 α \alpha α值二值化显著影响了注意力分数——它加强了query与每个key-value段最后元素的交互,并削弱了与中间元素的交互,中间元素在推理期间被丢弃。事实上,当 α ∈ { 0 , 1 } \alpha \in \{0, 1\} α∈{0,1}时,矩阵充满了0或 − ∞ -\infty −∞值,并且完全对应于推理时间的query到key的注意力模式。
训练目标
模型被激励将KV Cache压缩到某个CR,从而增加预测的 α \alpha α值。我们不是为每个追加或累积决策 α \alpha α匹配期望的比率,而是计算一个全局的单边损失,作为所有决策之和与在期望的压缩比(CR)下所有层 l l l、头 h h h和时间步 t t t的KV tokens的期望总和之间的差值,归一化为 ( n l n h n ) (n_l n_h n) (nlnhn):
ℓ C R = 1 n l n h n ∗ max ( 0 , ∑ l = 1 n l ∑ h = 1 n h ∑ t = 1 n ( 1 − α l h t ) − n l n h n C R ) . ( 10 ) \ell_{CR} = \frac{1}{n_l n_h n} * \max \left(0, \sum_{l=1}^{n_l} \sum_{h=1}^{n_h} \sum_{t=1}^{n} (1 - \alpha_{lht}) - \frac{n_l n_h n}{CR} \right). \quad (10) ℓCR=nlnhn1∗max(0,l=1∑nlh=1∑nht=1∑n(1−αlht)−CRnlnhn).(10)
它被添加到语言建模损失项 ℓ L M = − ∑ t = 1 n log p θ ( x t ∣ x < t ) \ell_{LM} = - \sum_{t=1}^{n} \log p_\theta (x_t \mid x_{<t}) ℓLM=−∑t=1nlogpθ(xt∣x<t)中,最终的训练目标是:
arg
min
θ
ℓ
L
M
+
ℓ
C
R
.
(
11
)
\arg \min_\theta \ell_{LM} + \ell_{CR}. \quad (11)
argθminℓLM+ℓCR.(11)
重要的是,训练过程设计为缓慢提高目标CR并在过程中获取可随时使用的DMC检查点。这是可能的,因为所有超参数,如Gumbel-sigmoid采样温度和学习率,都不会衰减并在整个训练过程中保持不变。这种DMC属性的一个实际应用案例是,在一次运行中生成具有不同CR的一系列DMC检查点,然后选择一个具有期望的效率-性能权衡的检查点。
我个人理解是在计算attenton score矩阵的时候,对于标准的attention来说只有当矩阵中的 q i ∗ k j q_i * k_j qi∗kj接近0的时候才能说明i和j这两个token是相互注意的,也就是有强烈的语义关系。但是现在新插入了一项 l o g ( 1 − α t ) log(1-\alpha_t) log(1−αt)进来,并且是求和的方式(见下面的附录H),根据语言模型的特性,这个 α t \alpha_t αt只能尽量往0和1靠,对应的语义关系就是强烈相关和完全不相关,否则会影响最后模型的性能。这样就做到了paper中描述的只和每个key-value段最后元素的交互,并削弱了与中间元素的交互,中间元素在推理期间被丢弃。这样在推理的时候就可以压缩了。

0x3.3 实际考虑
DMC允许每个头学习自定义压缩,这导致KV缓存序列在各个头之间具有可变长度。这给在 n n n维张量中高效存储这些序列时带来了困难,因为在自回归生成期间,由于DMC的自适应压缩率,每个头的KV Cache将通过不同数量的token进行扩展。然而,使用PagedAttention可以轻松地将这些序列存储在内存中,而几乎没有开销,其中为每个头单独按需分配新page。在第5.2节中,我们展示了基于FlashAttention和PagedAttention的实现测得的延迟和吞吐量。
也就是说,DMC和FlashAttention和vLLM相兼容的,这也让他有一定的实用性可能。
0x4. 总结
读到这里对idea的把握就差不多了,实验部分就不说了。Paper的附录里面还提到一个limit,DMC这种方法针对已经训练好的model通过continue train来应用DMC,如果from scratch训练模型会崩,所以这个应该是相比于MLA的劣势,因为对于很大的model来说不是每个人都有资源去continue train一下model的。不过这个paper的思路还是蛮有意思的,所以就在这里给大家分享一下它的Idea。谢谢大家。