模拟滤波器和数字滤波器(一)
下面介绍模拟滤波器和数字滤波器的频率响应的异同,以及如何使用python地scipy.signal来绘制其频谱响应和冲激阶跃响应。在第二期将谈到如何设计模拟滤波器和数字滤波器。
在正文之间,应该介绍连续时间傅立叶变换(CTFT)和离散时间傅立叶变换(DTFT)。
- CTFT 连续时间信号的傅立叶变换
时域连续,且具有非周期性的函数,可以进行傅里叶变换,求出连续的非周期的频谱。
X ( ω ) = ∫ − ∞ ∞ x ( t ) e − j ω t d t x ( t ) = 1 2 π ∫ − ∞ ∞ X ( ω ) e j ω t d ω \Large \begin{aligned}X(\omega) &= \int_{-\infty}^\infty x(t)e^{-j \omega t}dt \\ x(t) &= \frac{1}{2\pi}\int_{-\infty}^\infty X(\omega)e^{j \omega t}d\omega \end{aligned} X(ω)x(t)=∫−∞∞x(t)e−jωtdt=2π1∫−∞∞X(ω)ejωtdω
- DTFT 离散时间信号的傅立叶变换
时域离散,且具有非周期性的函数,可以求出连续的周期的频谱。周期为 2 π 2\pi 2π
X ( ω ) = ∑ − ∞ ∞ x [ n ] e − j ω n x [ n ] = 1 2 π ∫ − π π X ( ω ) e j ω n d ω \Large \begin{aligned}X(\omega) &= \sum_{-\infty}^\infty x[n]e^{-j \omega n} \\ x[n] &= \frac{1}{2\pi}\int_{-\pi}^\pi X(\omega)e^{j \omega n}d\omega \end{aligned} X(ω)x[n]=−∞∑∞x[n]e−jωn=2π1∫−ππX(ω)ejωndω
最大的区别是,连续时间信号的频谱从0到无穷大,离散时间信号的频谱从0到 2 π 2\pi 2π
下面将介绍python当中的模拟和数字滤波器。
1、模拟滤波器
比如一个二阶系统,其传递函数为:
H
(
s
)
=
u
d
n
f
2
s
2
+
2
∗
u
d
n
f
∗
d
r
∗
s
+
u
d
n
f
2
=
0
s
2
+
0
s
+
1
s
2
+
1
s
+
1
H(s) = \frac{udnf^2}{s^2+2*udnf*dr*s+udnf^2} = \frac{0s^2+0s+1}{s^2+1s+1}
H(s)=s2+2∗udnf∗dr∗s+udnf2udnf2=s2+1s+10s2+0s+1
该传递函数的时域微分形式为:
d
2
y
(
t
)
d
t
2
+
2
ζ
w
n
d
y
(
t
)
d
t
+
w
n
2
y
(
t
)
=
w
n
2
x
(
t
)
\frac{d^2y(t) }{dt^2} + 2\zeta w_n \frac{dy(t)}{dt} + w_n^2y(t) = w_n^2x(t)
dt2d2y(t)+2ζwndtdy(t)+wn2y(t)=wn2x(t)
import numpy as np
from scipy.signal import freqs_zpk,freqs,tf2zpk
import matplotlib.pyplot as plt
dr = 1/2 # damping ratio
udnf = 1 # undamped natural frequency
b = [0,0,udnf**2]
a = [1,2*udnf*dr,udnf**2]
z,p,k = tf2zpk(b,a)
w, h = freqs_zpk(z, p, k, worN=np.logspace(-3, 5, 1000))
fig = plt.figure(figsize=(14,7))
ax1 = fig.add_subplot(1, 1, 1)
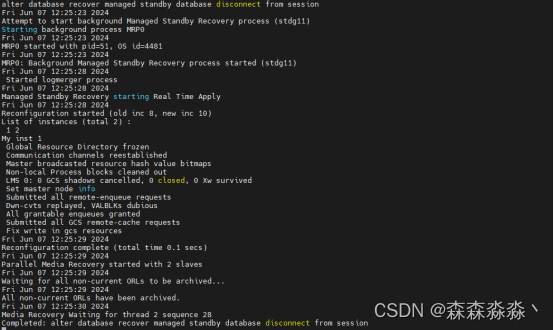
ax1.set_title('Analog filter frequency response')
ax1.semilogx(w, 20 * np.log10(abs(h)), 'b')
ax1.set_ylabel('Amplitude [dB]', color='b')
ax1.set_xlabel('Frequency [Hz]')
ax1.grid(True)
ax2 = ax1.twinx()
angles = np.unwrap(np.angle(h,deg=True),period=360)
ax2.semilogx(w, angles, 'g')
ax2.set_ylabel('Angle [degree]', color='g')
plt.axis('tight')
plt.show()
from scipy.signal import impulse,step
print(z,p,k)
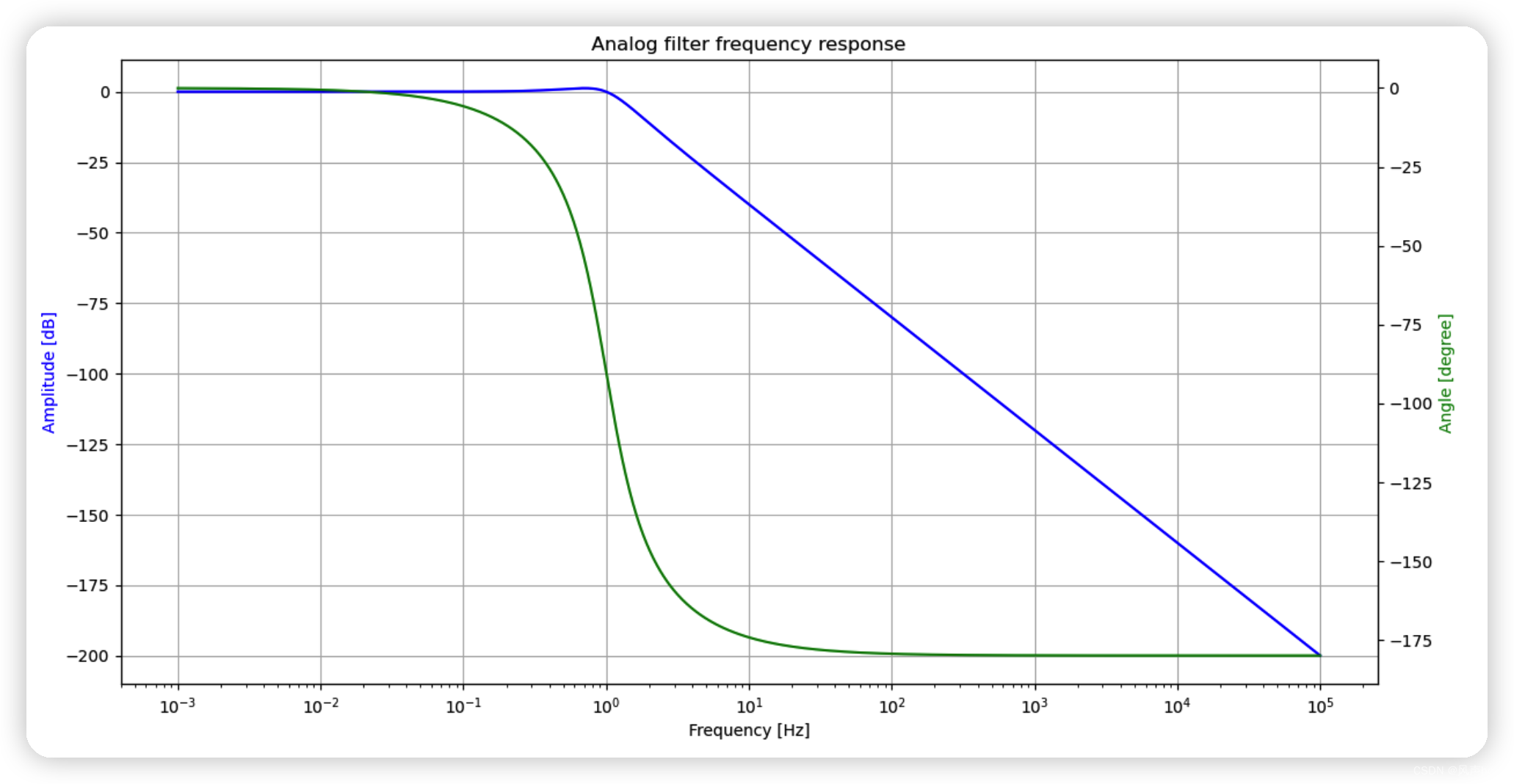
t, y = impulse((z,p,k))
t1, y1 = step((z,p,k))
plt.plot(t,y)
plt.plot(t1,y1)
plt.legend(["impulse response","step response"])
plt.show()
上面用到scipy.signal三个函数:
-
freqs_zpk:基于零极点的模拟频率响应。
- worN:频率轴范围。
- np.logspace:生成对数序列
-
freqs:基于有理传递函数的模拟频率响应。在本例中没有用到。尤其注意b、a对应传递函数是正幂。
b[0]*(jw)**M + b[1]*(jw)**(M-1) + ... + b[M] H(w) = ---------------------------------------------- a[0]*(jw)**N + a[1]*(jw)**(N-1) + ... + a[N] -
tf2zpk:传递函数转零极点表示。
2、数字滤波器
比如一个二阶系统:
H
(
z
)
=
1
1
−
(
2
r
cos
(
θ
)
z
−
1
+
r
2
z
−
2
=
z
2
z
2
−
(
2
r
cos
(
θ
)
z
+
r
2
H(z) = \frac{1}{1-(2r\cos(\theta)z^{-1}+r^2z^{-2}} = \frac{z^2}{z^2-(2r\cos(\theta)z+r^2}
H(z)=1−(2rcos(θ)z−1+r2z−21=z2−(2rcos(θ)z+r2z2
其单位脉冲响应为:
h
[
n
]
=
r
n
sin
(
n
+
1
)
θ
sin
θ
u
[
n
]
h[n] = r^n\frac{\sin(n+1)\theta}{\sin\theta}u[n]
h[n]=rnsinθsin(n+1)θu[n]
差分方程表示为:
y
[
n
]
−
2
r
cos
(
θ
)
y
[
n
−
1
]
+
r
2
y
[
n
−
2
]
=
x
[
n
]
y[n]-2r\cos(\theta)y[n-1]+r^2y[n-2] = x[n]
y[n]−2rcos(θ)y[n−1]+r2y[n−2]=x[n]
import numpy as np
from scipy.signal import freqz_zpk,freqz,tf2zpk
import matplotlib.pyplot as plt
fs = 2*np.pi
r = 3/4
theta = 45/180*np.pi
b = [1,0,0]
a = [1,-2*r*np.cos(theta),r**2]
z,p,k = tf2zpk(b,a)
w, h = freqz_zpk(z, p, k, worN=np.linspace(-2.5*np.pi,2.5*np.pi,1000),fs=fs)
fig = plt.figure(figsize=(14,7))
ax1 = fig.add_subplot(1, 1, 1)
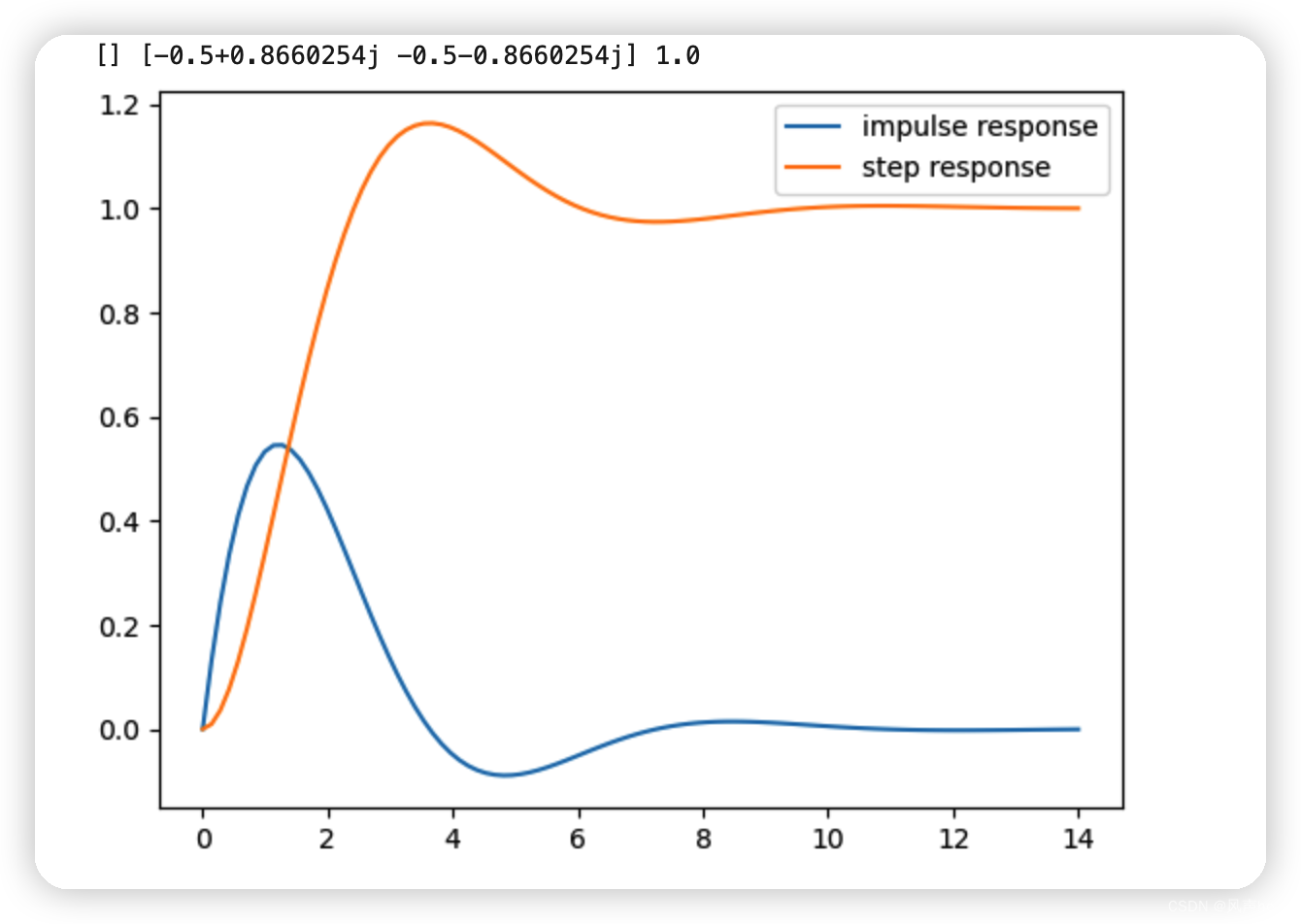
ax1.set_title('Digital filter frequency response')
ax1.plot(w, 20 * np.log10(abs(h)), 'b')
ax1.set_ylabel('Amplitude [dB]', color='b')
ax1.set_xlabel('w(radians)')
ax1.set_xticks([-3*np.pi,-2*np.pi,-1*np.pi,0,1*np.pi,2*np.pi,3*np.pi],
[r"$-3\pi$",r"$-2\pi$",r"$-\pi$","0",r"$\pi$",r"$2\pi$",r"$3\pi$"])
ax1.grid(True)
ax2 = ax1.twinx()
angles = np.unwrap(np.angle(h,deg=True),period=360)
ax2.plot(w, angles, 'g')
ax2.set_ylabel('Angle [degree]', color='g')
plt.axis('tight')
plt.show()
print(z,p,k)
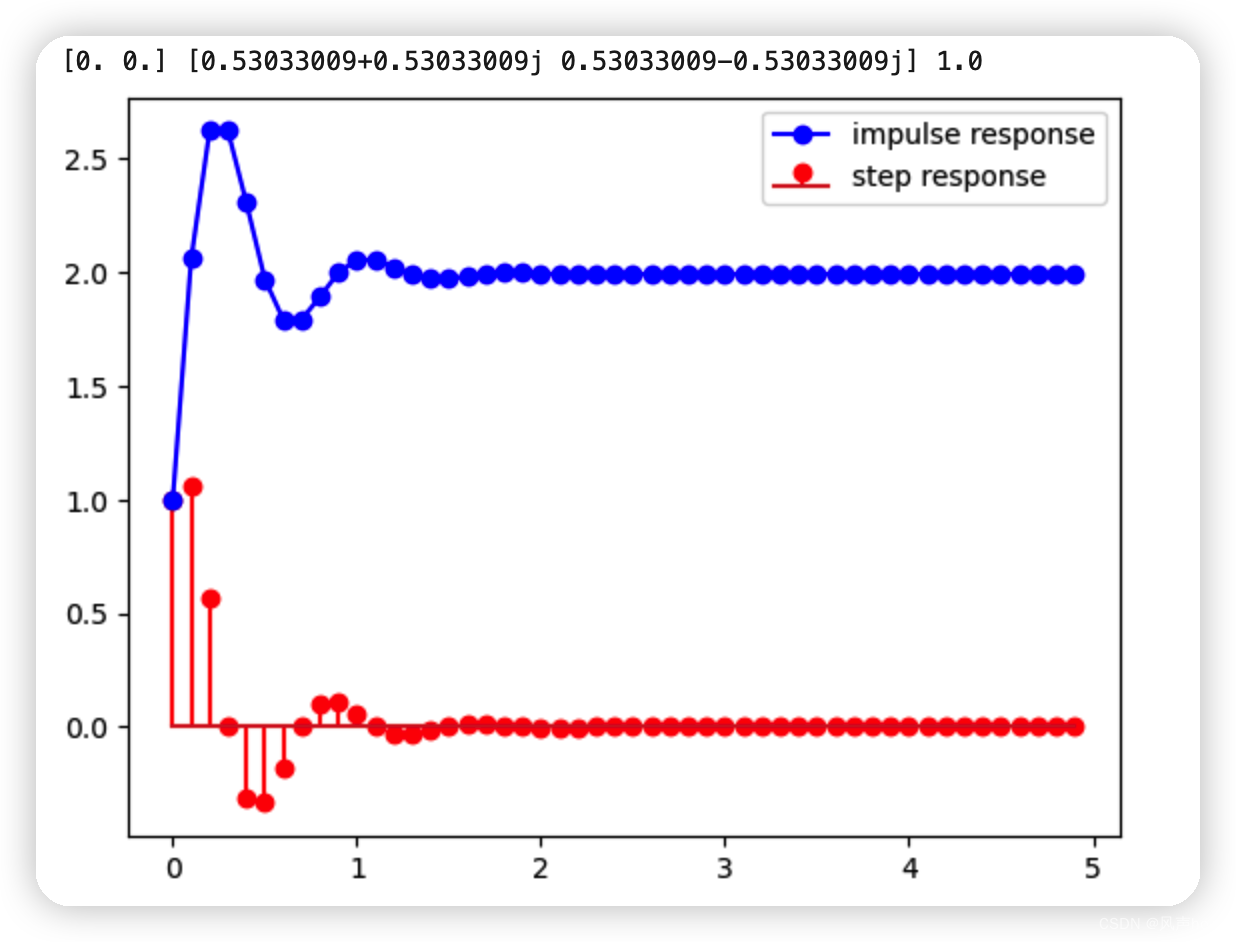
from scipy.signal import dimpulse, dstep
dt = 0.1
t, y = dimpulse((z,p,k,dt), n=50)
t1, y1 = dstep((z,p,k,dt), n=50)
plt.stem(t,np.squeeze(y),'r')
plt.plot(t1,np.squeeze(y1),'bo-')
plt.legend(["impulse response","step response"])
plt.show()
需要注意:
-
freqs_zpk:没有采样率这个概念,worN的单位就是Hz
-
freqz_zpk:有采样率这个概念,fs的默认值为 2 π 2\pi 2π,此时横坐标的单位为弧度。
-
freqz:使用传递函数绘制频谱响应。在
scipy.signal的定义里面,此函数为负幂。jw -jw -jwM jw B(e ) b[0] + b[1]e + ... + b[M]e H(e ) = ------ = ----------------------------------- jw -jw -jwN A(e ) a[0] + a[1]e + ... + a[N]e -
弧度和频率换算举例:设置 w o r N = [ − 2 π , 2 π ] worN=[-2\pi,2\pi] worN=[−2π,2π],如果fs使用默认值 2 π H z 2\pi Hz 2πHz,那么实际横坐标的范围为 [ − 2 π , 2 π ] [-2\pi,2\pi] [−2π,2π],即两个周期;如果fs使用 π H z \pi Hz πHz,那么实际的横坐标范围为 [ − 4 π , 4 π ] [-4\pi,4\pi] [−4π,4π]。其中 π \pi π弧度对应 f s / 2 fs/2 fs/2 Hz.








![[ssi-uploader插件]解决如何接收服务器返回数据+修改参数名称](https://img-blog.csdnimg.cn/direct/bedde53ae52a42dd81c57895b2c87f15.png)