以Resnet50作为主干网络，然后使用GCN逐层聚合多级特征，逐级聚合这种模型架构早已不新鲜，这篇文章使用GCN的方式对特征进行聚合，没有代码。这篇文章没有过多的介绍如何构造的节点特征和邻接矩阵，我觉得对于图卷积来说，最重要的一点就是确定那些特征作为图节点以及节点直接的连接关系。

很多方法是直接将特征图的每个像素作为一个节点，那这样的话怎么确定每个像素之间的连接关系呢？

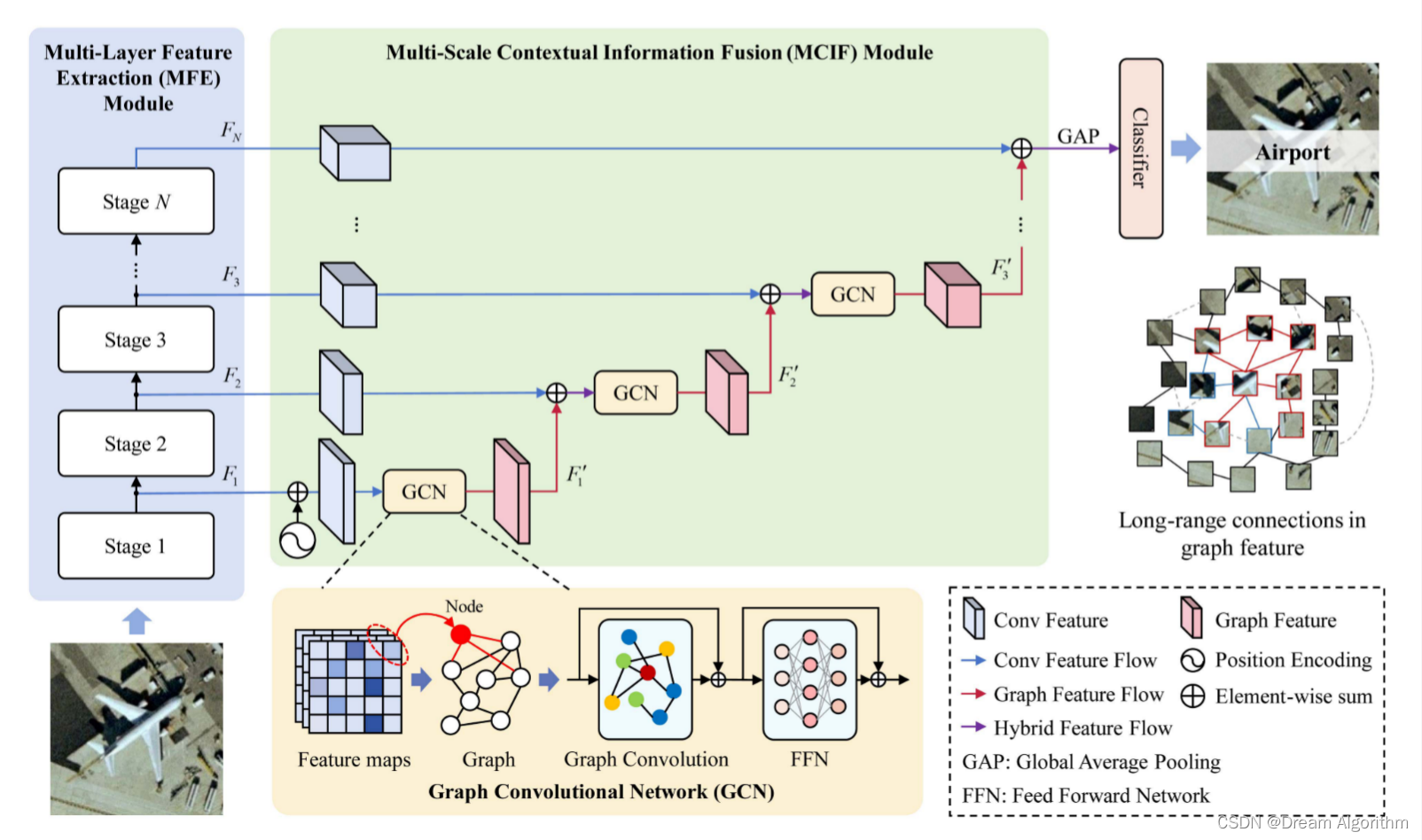
对于邻接矩阵来说，两个节点相连置为一，两个节点不相连置为零，通过将节点矩阵和邻接矩阵进行相乘来进行节点之间的信息交互。这种交互是只要两个节点之间相连就将两个节点的特征值进行相加。

这种直接相加的方式忽略了节点与节点之间的重要程度，可以使用图注意力来给图的节点与节点之间施加一个权重，这个权重可以通过自注意力的方式得到，也可以通过图注意力网络中的计算方式得到节点与节点之间的权重关系。图注意力网络的代码如下：

import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import networkx as nx
 
 
def get_weights(size, gain=1.414):
    weights = nn.Parameter(torch.zeros(size=size))
    nn.init.xavier_uniform_(weights, gain=gain)
    return weights
 
class GraphAttentionLayer(nn.Module):
    '''
    Simple GAT layer 图注意力层 (inductive graph)
    '''
    def __init__(self, in_features, out_features, dropout, alpha, concat = True, head_id = 0):
        ''' One head GAT '''
        super(GraphAttentionLayer, self).__init__()
        self.in_features = in_features  #节点表示向量的输入特征维度
        self.out_features = out_features    #节点表示向量的输出特征维度
        self.dropout = dropout  #dropout参数
        self.alpha = alpha  #leakyrelu激活的参数
        self.concat = concat    #如果为true，再进行elu激活
        self.head_id = head_id  #表示多头注意力的编号
 
        self.W_type = nn.ParameterList()
        self.a_type = nn.ParameterList()
        self.n_type = 1 #表示边的种类
        for i in range(self.n_type):
            self.W_type.append(get_weights((in_features, out_features)))
            self.a_type.append(get_weights((out_features * 2, 1)))
 
        #定义可训练参数，即论文中的W和a
        self.W = nn.Parameter(torch.zeros(size = (in_features, out_features)))
        nn.init.xavier_uniform_(self.W.data, gain = 1.414)  #xavier初始化
        self.a = nn.Parameter(torch.zeros(size = (2 * out_features, 1)))
        nn.init.xavier_uniform_(self.a.data, gain = 1.414)  #xavier初始化
 
        #定义dropout函数防止过拟合
        self.dropout_attn = nn.Dropout(self.dropout)
        #定义leakyrelu激活函数
        self.leakyrelu = nn.LeakyReLU(self.alpha)
 
    def forward(self, node_input, adj, node_mask = None):
        '''
        node_input: [batch_size, node_num, feature_size] feature_size 表示节点的输入特征向量维度
        adj: [batch_size, node_num, node_num] 图的邻接矩阵
        node_mask:  [batch_size, node_mask]
        '''
 
        zero_vec = torch.zeros_like(adj)
        scores = torch.zeros_like(adj)
 
        for i in range(self.n_type):
            h = torch.matmul(node_input, self.W_type[i])
            h = self.dropout_attn(h)
            N, E, d = h.shape   # N == batch_size, E == node_num, d == feature_size
 
            a_input = torch.cat([h.repeat(1, 1, E).view(N, E * E, -1), h.repeat(1, E, 1)], dim = -1)
            a_input = a_input.view(-1, E, E, 2 * d)     #([batch_size, E, E, out_features])
 
            score = self.leakyrelu(torch.matmul(a_input, self.a_type[i]).squeeze(-1))   #([batch_size, E, E, 1]) => ([batch_size, E, E])
            #图注意力相关系数（未归一化）
 
            zero_vec = zero_vec.to(score.dtype)
            scores = scores.to(score.dtype)
            scores += torch.where(adj == i+1, score, zero_vec.to(score.dtype))
 
        zero_vec = -1*30 * torch.ones_like(scores)  #将没有连接的边置为负无穷
        attention = torch.where(adj > 0, scores, zero_vec.to(scores.dtype))    #([batch_size, E, E])
        # 表示如果邻接矩阵元素大于0时，则两个节点有连接，则该位置的注意力系数保留；否则需要mask并置为非常小的值，softmax的时候最小值不会被考虑
 
        if node_mask is not None:
            node_mask = node_mask.unsqueeze(-1)
            h = h * node_mask   #对结点进行mask
 
        attention = F.softmax(attention, dim = 2)   #[batch_size, E, E], softmax之后形状保持不变，得到归一化的注意力权重
        h = attention.unsqueeze(3) * h.unsqueeze(2) #[batch_size, E, E, d]
        h_prime = torch.sum(h, dim = 1)             #[batch_size, E, d]
 
        # h_prime = torch.matmul(attention, h)    #[batch_size, E, E] * [batch_size, E, d] => [batch_size, N, d]
 
        #得到由周围节点通过注意力权重进行更新的表示
        if self.concat:
            return F.elu(h_prime)
        else:
            return h_prime
 
class GAT(nn.Module):
    def __init__(self, in_dim, hid_dim, dropout, alpha, n_heads, concat = True):
        '''
        Dense version of GAT
        in_dim输入表示的特征维度、hid_dim输出表示的特征维度
        n_heads 表示有几个GAL层，最后进行拼接在一起，类似于self-attention从不同的子空间进行抽取特征
        '''
        super(GAT, self).__init__()
        assert hid_dim % n_heads == 0
        self.dropout = dropout
        self.alpha = alpha
        self.concat = concat
 
        self.attn_funcs = nn.ModuleList()
        for i in range(n_heads):
            self.attn_funcs.append(
                #定义multi-head的图注意力层
                GraphAttentionLayer(in_features = in_dim, out_features = hid_dim // n_heads,
                                    dropout = dropout, alpha = alpha, concat = concat, head_id = i)
            )
 
        self.dropout = nn.Dropout(self.dropout)
 
    def forward(self, node_input, adj, node_mask = None):
        '''
        node_input: [batch_size, node_num, feature_size]    输入图中结点的特征
        adj:    [batch_size, node_num, node_num]    图邻接矩阵
        node_mask:  [batch_size, node_num]  表示输入节点是否被mask
        '''
        hidden_list = []
        for attn in self.attn_funcs:
            h = attn(node_input, adj, node_mask = node_mask)
            hidden_list.append(h)
 
        h = torch.cat(hidden_list, dim = -1)
        h = self.dropout(h) #dropout函数防止过拟合
        x = F.elu(h)     #激活函数
        return x
 
 
#特征矩阵
x = torch.randn((2, 4, 8))
#邻接矩阵
adj = torch.tensor([[[0, 1, 0, 1],
                    [1, 0, 1, 0],
                    [0, 1, 0, 1],
                    [1, 0, 1, 0]]])
adj = adj.repeat(2, 1, 1)
#mask矩阵
node_mask = torch.Tensor([[1, 0, 0, 1],
                          [0, 1, 1, 1]])
 
 
gat_layer = GraphAttentionLayer(in_features = 8, out_features = 8, dropout = 0.1, alpha = 0.2, concat = True)  #输入特征维度8， 输出特征维度8， 使用多头注意力机制
gat_ = GAT(in_dim = 8, hid_dim = 8, dropout = 0.1, alpha = 0.2, n_heads = 2, concat = True)    #输入特征维度8， 输出特征维度8, 使用多头注意力机制
 
output_ = gat_(x, adj, node_mask)
print(output_.shape)  
 
output_ = gat_(x, adj, node_mask)
print(output_.shape)
 
 
#输出：
torch.Size([2, 4, 8])
torch.Size([2, 4, 8])

自注意力和图注意力在计算节点之间权重的方式稍有不同，在自注意力的计算方式中之进行了矩阵相乘并没有可训练的参数。在图注意力计算节点之间权重时，采用了线性映射的方式，这两种权重计算方式那个更好一点还要通过实验来进行验证。