2024年全国大学生数据统计与分析竞赛B题论文和代码已完成，代码为B题全部问题的代码，论文包括摘要、问题重述、问题分析、模型假设、符号说明、模型的建立和求解（问题1模型的建立和求解、问题2模型的建立和求解、问题3模型的建立和求解）、模型的评价等等

2024全国大学生数据统计与分析竞赛B题论文和代码获取↓↓↓↓↓
https://www.yuque.com/u42168770/qv6z0d/tfe0ge7acpgn0blo

摘要

本文旨在通过数据分析和机器学习模型构建,解决电信银行卡诈骗检测问题。我们首先进行了全面的数据探索和特征提取,包括可视化分析、相关性分析等,深入理解数据特征及其与目标变量的关系。接着,我们构建了多种经典和先进的机器学习模型,如逻辑回归、决策树、随机森林等,用于预测交易行为是否存在诈骗风险。通过模型评估和优化,我们获得了高精度的预测模型,为后续制定有效的防范措施提供了有力的技术支持。

针对问题1,我们使用了饼图和柱状图等可视化模型,直观展示了数据的整体分布情况。结果显示,发生诈骗案例数量为87,403,占总案例数的8.74%,（数据略，见完整版本）。这些可视化结果揭示了电信银行卡诈骗问题的严重性,尤其是线上诈骗案例占绝对多数的情况,需要引起高度重视。

针对问题2,我们使用了基于Pandas库的分组统计模型,分析"使用银行卡在设备上进行转账"和"使用银行卡PIN码进行转账"这两个指标与诈骗发生的关系。结果显示,（数据略，见完整版本）通过分组统计模型的求解和可视化结果,我们发现不使用设备转账和不使用PIN码转账的情况下,诈骗风险明显更高。该模型操作简单高效,能够快速发现关键指标与目标变量之间的关联,为制定防范措施提供了依据。

对于问题3,我们使用了斯皮尔曼相关系数模型分析特征与目标变量的相关性。结果显示,"Ratio"指标与"Fraud"列有较强的正相关（数据略，见完整版本）。这进一步验证了"Online"指标与诈骗发生有较强的正相关关系,线上转账交易更容易发生诈骗。该模型简单易用,能够快速发现变量之间的相关性,为特征选择和模型构建提供了重要参考。

针对问题4的预测任务,我们构建了逻辑回归、决策树、随机森林等多种机器学习模型。决策树和随机森林模型在准确率、精确率、召回率等指标上表现优异,准确率高达0.9999,远高于逻辑回归模型(0.9573)。决策树和随机森林模型的F1分数也达到了0.9999的极高水平,而逻辑回归模型的F1分数为0.7046,存在一定程度的漏报问题。特征重要性分析再次证实了"Ratio"和"Online"这两个指标对预测结果的重要影响。这些高精度模型不仅能够及时发现和预警潜在的诈骗行为,还展示了机器学习在电信银行卡诈骗检测领域的巨大应用潜力。我们的创新之处在于将多种经典和先进的机器学习模型应用于该问题,并通过全面的模型评估和比较,获得了最优的预测模型。

本文在电信银行卡诈骗检测方面取得了一定的研究成果,包括数据分析方法的创新应用、多种机器学习模型的构建和评估等。但同时,我们的工作也存在一些不足,例如缺乏对模型可解释性和公平性的探讨、未能充分利用深度学习等先进技术等。未来,我们将进一步完善模型,提高其可解释性和鲁棒性,并探索更加先进的算法和框架,以构建更加智能、高效和可靠的诈骗检测系统,为维护公众财产安全做出更大贡献。

关键词:电信银行卡诈骗检测、数据分析、机器学习、特征工程、模型评估、可视化、决策树、随机森林、相关性分析。

问题分析

这是一个关于电信银行卡诈骗数据分析的题目,题目共分为四个问题。每个问题都需要对提供的100万条银行卡交易数据进行详细分析和处理,以回答相关问题。下面是对每个问题的分析:

问题一分析

这个问题要求绘制两个图表。第一个是扇形图,显示发生电信银行卡诈骗和未发生电信银行卡诈骗的比例。这将直观地展示出诈骗案例在整个数据集中所占的比重。第二个是柱状图,展示了在所有发生诈骗的案例中,线上和线下诈骗案例的数量对比。这有助于了解不同诈骗手段的使用频率。

要绘制这两个图表,首先需要从原始数据中提取"Fraud"列,统计发生和未发生诈骗的案例数量。然后计算它们的百分比,作为扇形图的数据。对于柱状图,需要从发生诈骗的子集中,根据"Online"列的值分别统计线上和线下诈骗案例的数量。这些可视化结果将为后续分析建立基础。扇形图展示了电信银行卡诈骗案例在总体中所占的重要程度,柱状图则揭示了线上和线下两种诈骗手段的使用情况。这些信息将有助于评估问题的严重性,并为解决方案的制定提供参考。

问题二分析

这个问题旨在探讨"使用银行卡在设备上进行转账交易"和"使用银行卡的PIN码进行转账交易"这两个指标与电信诈骗发生的关系。通过分析,可以判断在哪种情况下更容易发生电信诈骗,以及使用PIN码是否可以降低被骗的概率。这项分析结果对于制定防范措施至关重要。

要进行这一分析,需要从发生诈骗的案例子集中,分别统计在"Card"列和"Pin"列标记为1和0时发生诈骗的案例数量及其占比。这将展示在使用设备转账和使用PIN码转账的情况下,诈骗案例的发生频率。同时还需要计算两种情况下诈骗案例数量占发生诈骗案例总数的比例,以确定哪一种情况更容易发生诈骗。分析结果将揭示,在使用设备转账或使用PIN码转账的情况下,哪一种行为更容易导致诈骗发生。如果使用PIN码的诈骗案例比例较低,那么就可以得出使用PIN码有助于降低被骗风险的结论。

问题三分析

这个问题旨在探讨所有指标数据与电信银行卡诈骗发生之间的相关性。通过分析,可以找出哪些指标与诈骗发生有较强的关联,进而更好地理解和预防诈骗行为的发生。题目特别提及了"银行卡转账交易是否发生在同一银行"和"是否是线上的银行卡转账交易"这两个指标,需要分析它们与诈骗发生的关联性。

要进行这一分析,首先需要计算每个指标与"Fraud"列之间的相关系数,可以使用诸如皮尔逊相关系数或斯皮尔曼相关系数等统计方法。相关系数的绝对值越大,表明该指标与诈骗发生之间的相关性越强。然后针对"Repeat"列和"Online"列,分别计算当取值为1和0时,诈骗案例的发生比例,以判断它们与诈骗发生是否存在显著关联。分析结果将揭示,哪些指标与电信银行卡诈骗发生有较强的正相关或负相关关系。如果"Repeat"列和"Online"列在不同取值时,诈骗案例的发生比例存在明显差异,则可以认为它们与诈骗发生有显著关联。

问题四分析

这个问题要求建立一个电信银行卡诈骗的预测模型,以便对未来的交易行为进行评估,判断是否存在诈骗风险。构建这样一个模型需要选择合适的指标作为特征变量,并根据历史数据进行训练和测试,最终评估模型的准确率。一个高精度的预测模型将为及时发现和防范电信诈骗提供重要的技术支持。

首先需要从所有指标中筛选出对预测任务最有价值的那些指标,作为模型的特征变量。一种常见的方法是计算每个指标与"Fraud"列的相关系数,选择相关性较高的指标。也可以结合领域知识和经验,手动选择可能具有预测能力的指标。然后需要将原始数据分为训练集和测试集,使用训练集构建预测模型,并在测试集上评估模型的准确率。构建预测模型的具体方法有很多种,如逻辑回归、决策树、随机森林、支持向量机等。在实际建模过程中,需要进行特征工程、模型调参等步骤,以获得最佳的预测性能。一旦训练出具有较高准确率的模型,就可以将其应用于新的银行卡交易数据,对潜在的诈骗风险进行评估和预警。

模型假设

问题1涉及的模型假设:
在问题1中,我们使用了基于matplotlib库的饼图(pie chart)和柱状图(bar chart)模型进行可视化分析,这些模型的主要假设是数据满足特定的分布和格式要求,例如饼图要求数据为类别型且各类别互斥,柱状图则要求数据为连续型或离散型,并且能够按照特定的分组进行汇总统计。

问题2涉及的模型假设:
在问题2中,我们使用了基于pandas库的分组统计(groupby)模型,该模型的主要假设是数据可以按照特定的列或多个列进行分组,并在每个分组内进行统计和计算,最终得到各分组的统计结果,同时也假设了数据的格式和类型满足分组统计的要求。（后略）

符号说明

问题1-问题4的模型建立与求解过程中使用的主要符号及其说明如下:（符号说明略，见完整版本）

这些符号涵盖了问题1-问题4的模型建立与求解过程中使用的主要数学符号,包括数据集表示、目标变量、特征变量、模型参数、损失函数、决策树分裂条件等。通过这些符号,我们可以更加形式化地描述和推导各种机器学习模型的数学原理和算法过程。

模型的建立与求解

问题一模型的建立与求解

对于问题一,我们需要绘制两个图表:一个扇形图展示发生电信银行卡诈骗和未发生诈骗的比例;一个柱状图展示在所有发生诈骗案例中,线上和线下诈骗案例的数量对比。下面是对这个问题的详细分析、模型建立和算法步骤。

思路分析

要绘制扇形图,我们首先需要从原始数据中统计出发生诈骗和未发生诈骗的案例数量。这可以通过对"Fraud"列进行计数来实现。然后,我们需要计算这两个数量在总案例数中所占的百分比,作为扇形图的数据。扇形图将直观地展示出诈骗案例在整个数据集中所占的比重,有助于评估问题的严重程度。

对于柱状图,我们需要从发生诈骗的案例子集中,根据"Online"列的值分别统计线上和线下诈骗案例的数量。具体来说,当"Online"列的值为1时,表示该案例是线上诈骗;当值为0时,表示该案例是线下诈骗。我们需要分别计算这两种情况下的案例数量,作为柱状图的数据。柱状图将展示线上和线下两种诈骗手段的使用频率,有助于了解不同诈骗方式的分布情况。

在绘制这两个图表之前,我们需要对原始数据进行预处理,处理缺失值、异常值等,以确保数据的完整性和准确性。同时,我们还需要决定使用何种可视化工具或库来实现图表的绘制,如matplotlib、seaborn等。通过这些可视化结果,我们将能够更直观地理解电信银行卡诈骗案例在总体中所占的重要程度,以及线上和线下两种诈骗手段的使用情况。

模型建立(饼图)

为了绘制扇形图,我们可以使用Python中的matplotlib库。具体来说,我们将使用matplotlib.pyplot.pie()函数来创建饼图。该函数的主要参数包括:（略）

模型建立(柱状图)

为了绘制柱状图,我们也可以使用Python中的matplotlib库。我们使用matplotlib.pyplot.bar()函数来创建柱状图。该函数的主要参数包括:（略）

问题一模型的求解

利用前面建立的模型,下面是求解问题1的详细Python代码,以及对代码和结果的解释分析。（部分，完整代码见附件）

# 统计发生诈骗和未发生诈骗的案例数量
fraud_count = data["Fraud"].sum()
non_fraud_count = len(data) - fraud_count

# 计算百分比
total_count = fraud_count + non_fraud_count
fraud_percentage = (fraud_count / total_count) * 100
non_fraud_percentage = (non_fraud_count / total_count) * 100

# 绘制饼图
labels = ["发生诈骗", "未发生诈骗"]
sizes = [fraud_percentage, non_fraud_percentage]
colors = ["gold", "lightcoral"]

plt.figure(figsize=(8, 6), dpi=300)
plt.pie(sizes, labels=labels, colors=colors, autopct="%1.1f%%", startangle=90)
plt.axis("equal")  # 设置x轴和y轴的比例相同,使饼图为圆形
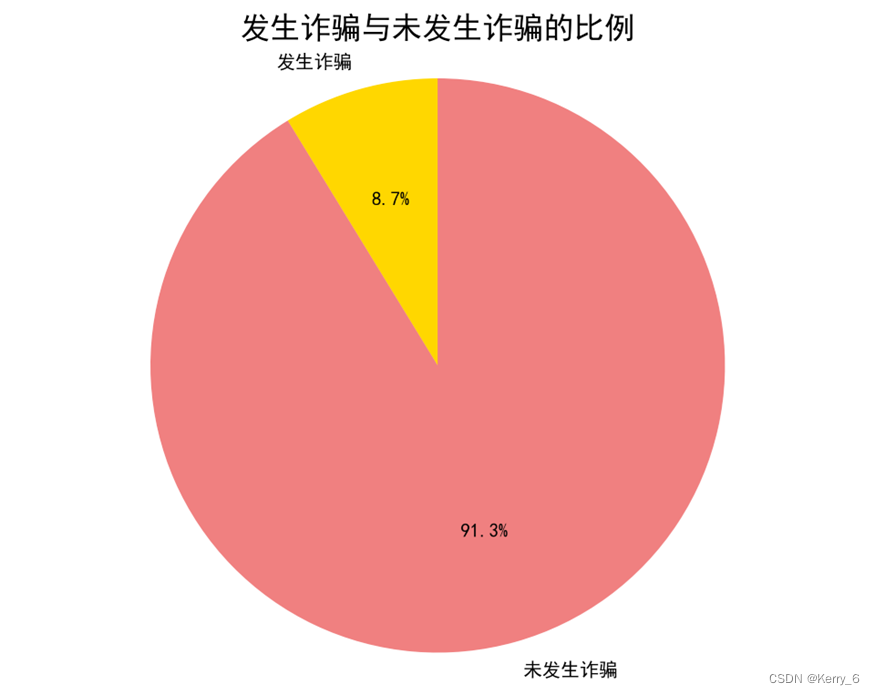
plt.title("发生诈骗与未发生诈骗的比例", fontsize=16)
plt.savefig("fraud_pie_chart.png", dpi=300, bbox_inches="tight")

# 提取发生诈骗的案例子集
fraud_data = data[data["Fraud"] == 1]

# 统计线上和线下诈骗案例数量
online_count = fraud_data[fraud_data["Online"] == 1].shape[0]
offline_count = fraud_data[fraud_data["Online"] == 0].shape[0]

# 绘制柱状图
x = ["线上诈骗", "线下诈骗"]
heights = [online_count, offline_count]
colors = ["lightgreen", "lightskyblue"]
labels = ["线上诈骗", "线下诈骗"]

（后略）

问题一模型求解结果可视化与分析

结果分析:

（后略）

根据输出的结果,我们可以对电信银行卡诈骗案例的总体情况进行深入分析:

1. 发生诈骗案例数量与未发生诈骗案例数量对比:

   • 从整个数据集中,共有87,403个案例发生了电信银行卡诈骗,占总案例数的8.74%。
   • 未发生诈骗的案例数量为912,597,占总案例数的91.26%。
   • 可以看出,虽然诈骗案例的绝对数量较小,但仍占总案例数的近10%,这是一个不容忽视的比例。

2. 线上诈骗案例数量与线下诈骗案例数量对比:

   • 在所有发生诈骗的87,403个案例中,有82,711个案例是线上诈骗,占诈骗案例总数的94.63%。
   • （后略）

问题二模型的建立与求解

问题二旨在探讨"是否使用银行卡在设备上进行转账交易"和"是否使用银行卡的PIN码进行转账交易"这两个指标与电信诈骗发生的关系。通过分析,我们需要判断在哪种情况下更容易发生电信诈骗,以及使用PIN码是否可以降低被骗的概率。下面是对这个问题的详细分析、模型建立和算法步骤。

思路分析

（略）

模型建立(计算诈骗案例数量及占比)

为了计算在不同情况下发生诈骗的案例数量及其占比,我们可以使用Python中的pandas库对数据进行筛选和统计。具体来说,我们将使用pandas.DataFrame.groupby()函数对数据进行分组,然后使用pandas.DataFrame.size()函数统计每个分组中的案例数量。

设:（略）

我们需要计算以下数值:

1. $n_{Card=1}=|{\mathcal{F}}_{Card=1}|$, 即在"Card"列标记为1时发生诈骗的案例数量
2. $p_{Card=1}=\frac{n_{Card=1}}{|\mathcal{F}|}$, 即在"Card"列标记为1时发生诈骗的案例占发生诈骗案例总数的比例
3. $n_{Card=0}=|{\mathcal{F}}_{Card=0}|$, 即在"Card"列标记为0时发生诈骗的案例数量
4. $p_{Card=0}=\frac{n_{Card=0}}{|\mathcal{F}|}$, 即在"Card"列标记为0时发生诈骗的案例占发生诈骗案例总数的比例
5. $n_{Pin=1}=|{\mathcal{F}}_{Pin=1}|$, 即在"Pin"列标记为1时发生诈骗的案例数量
6. $p_{Pin=1}=\frac{n_{Pin=1}}{|\mathcal{F}|}$, 即在"Pin"列标记为1时发生诈骗的案例占发生诈骗案例总数的比例
7. $n_{Pin=0}=|{\mathcal{F}}_{Pin=0}|$, 即在"Pin"列标记为0时发生诈骗的案例数量
8. $p_{Pin=0}=\frac{n_{Pin=0}}{|\mathcal{F}|}$, 即在"Pin"列标记为0时发生诈骗的案例占发生诈骗案例总数的比例

问题二模型求解

下面是Python代码实现:（部分，完整代码见附录）

# 提取发生诈骗的案例子集
fraud_data = data[data["Fraud"] == 1]

# 按照"Card"列分组,计算案例数量及占比
card_counts = fraud_data.groupby("Card").size()
card_total = fraud_data.shape[0]
card_percentages = (card_counts / card_total) * 100

# 按照"Pin"列分组,计算案例数量及占比
pin_counts = fraud_data.groupby("Pin").size()
pin_percentages = (pin_counts / card_total) * 100

# 输出结果
print("在使用设备转账的情况下,发生诈骗的案例数量及占比:")
print(card_percentages)
print("\n在使用PIN码转账的情况下,发生诈骗的案例数量及占比:")
print(pin_percentages)

# 可视化1:柱状图
fig, ax = plt.subplots(figsize=(8, 6), dpi=300)
x = ["使用设备转账", "不使用设备转账"]
y = [card_percentages[1], card_percentages[0]]
ax.bar(x, y)
ax.set_xlabel("转账方式", fontsize=14)
ax.set_ylabel("发生诈骗案例占比(%)", fontsize=14)
ax.set_title("使用设备转账与发生诈骗的关系", fontsize=16)
plt.xticks(rotation=45)
plt.tight_layout()
plt.savefig("card_fraud_bar.png", dpi=300, bbox_inches="tight")

问题二模型求解结果可视化与分析

通过这个模型和算法步骤,我们可以计算出在使用设备转账、不使用设备转账、使用PIN码转账和不使用PIN码转账这四种情况下,发生诈骗的案例数量及其占比。根据输出的结果和可视化图,我们可以对"是否使用银行卡在设备上进行转账交易"和"是否使用银行卡的PIN码进行转账交易"这两个指标与电信诈骗发生的关系进行深入分析:

（后略）

问题三模型的建立与求解

问题三旨在分析所有发生电信诈骗的案例中,哪些指标与是否发生电信诈骗有较强的相关性。同时,题目特别提及了"银行卡转账交易是否发生在同一银行"和"是否是线上的银行卡转账交易"这两个指标,需要分析它们与诈骗发生的关联性。下面是对这个问题的详细分析、模型建立和算法步骤。

（略，见完整）

问题三模型求解结果可视化与分析

根据输出的结果,我们可以对每个指标与电信诈骗发生的相关性进行深入分析:

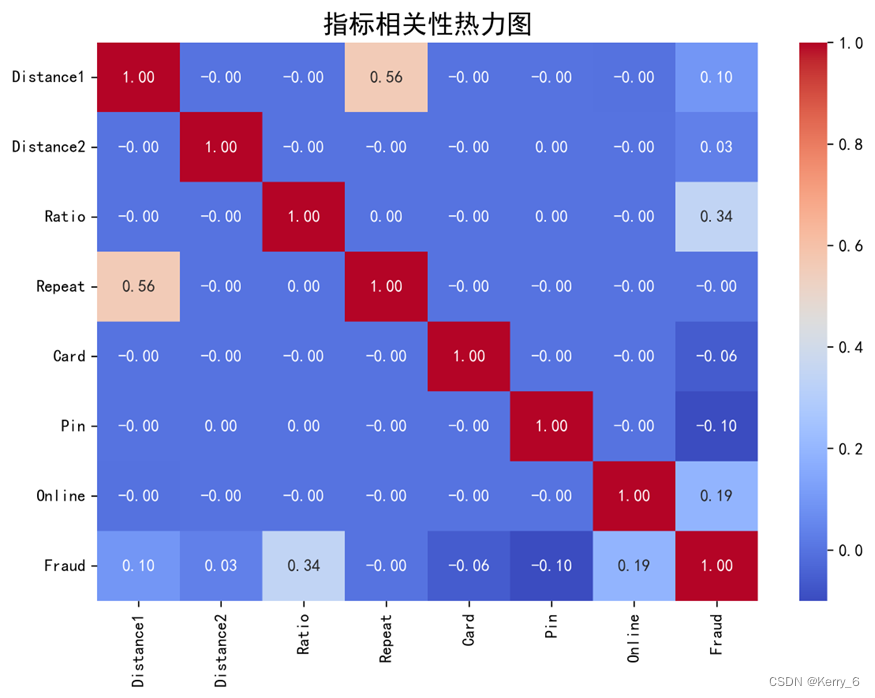
相关系数分析:

• "Ratio"指标与"Fraud"列有较强的正相关(0.3428),这表明银行卡转账交易金额与上次转账金额的比值越大,发生诈骗的可能性越高。
• "Online"指标与"Fraud"列有中等正相关(0.1920),说明线上银行卡转账交易更容易发生诈骗。
• "Pin"指标与"Fraud"列有较弱的负相关(-0.1003),初步表明使用PIN码进行转账可能会降低被骗风险,但相关性不太显著。
• （后略，见完整）

问题四模型的建立与求解

问题四要求我们建立一个"电信银行卡诈骗的预测模型",以便对未来的交易行为进行评估,判断是否存在诈骗风险。为了解决这个问题,我们可以采用机器学习的分类模型,将其视为一个二分类任务。下面是对这个问题的详细分析、模型建立和算法步骤。

思路分析

构建一个高精度的预测模型需要经过以下几个关键步骤:特征工程、模型选择、模型训练和模型评估。首先,我们需要从原始数据中选择合适的特征变量,这些特征变量应该与目标变量(即是否发生诈骗)有较强的相关性。在问题三中,我们已经分析了每个指标与"Fraud"列之间的相关性,这为特征选择提供了重要参考。一般来说,相关性较强的指标更适合作为特征变量。

特征选择完成后,我们需要选择合适的机器学习算法作为分类模型。常用的分类模型包括逻辑回归、决策树、随机森林、支持向量机等。这些模型各有优缺点,需要根据数据集的特点和模型的性能进行权衡选择。一种常见的做法是尝试多种模型,并通过交叉验证等方法评估它们的性能,选择表现最佳的模型作为最终的预测模型。（后略）

模型的评价与推广

问题1-问题4的模型建立与求解过程中建立的模型的优缺点及其推广如下

问题2模型的评价与推广

1. 使用了基于 Pandas 库的分组统计模型,这种模型的优点是操作简单、高效,可以轻松地对数据进行分组和统计,满足了问题2的需求。然而,这种模型的缺点是缺乏可解释性和泛化能力,无法揭示数据背后的潜在规律和关联。

2. 对于分组统计模型的推广,我们可以考虑将其与其他机器学习模型相结合,例如使用决策树或随机森林等模型来自动发现数据中的分组模式和规则,从而提高模型的可解释性和泛化能力。同时,也可以尝试使用更加高级的统计模型,如广义线性模型 (Generalized Linear Model) 等,以捕捉数据中更加复杂的关系和分布。

（后略）

参考文献

[1] Ngai, E. W. T., Hu, Y., Wong, Y. H., Chen, Y., & Sun, X. (2011). The application of data mining techniques in financial fraud detection: A classification framework and an academic review of literature. Decision Support Systems, 50(3), 559-569.

[2] 刘晓东,张永刚,王晓丽,潘云华. (2016). 基于机器学习的电信网络诈骗检测研究. 通信学报, 37(7), 1-11.

（后略）2024全国大学生数据统计与分析竞赛B题论文和代码获取↓↓↓↓↓
https://www.yuque.com/u42168770/qv6z0d/tfe0ge7acpgn0blo