目录

一·归并排序介绍：

二·归并排序递归版本：

2.1·递归思路：

2.2·递归代码实现：

三·归并排序非递归版本：

3.1·非递归思路：

3.2·非递归代码实现：

四·归并排序性能分析：

---

欢迎大佬：

羑悻的小杀马特-CSDN博客羑悻的小杀马特关注c++,c语言,数据结构领域.https://blog.csdn.net/2401_82648291?spm=1011.2266.3001.5343

一·归并排序介绍：

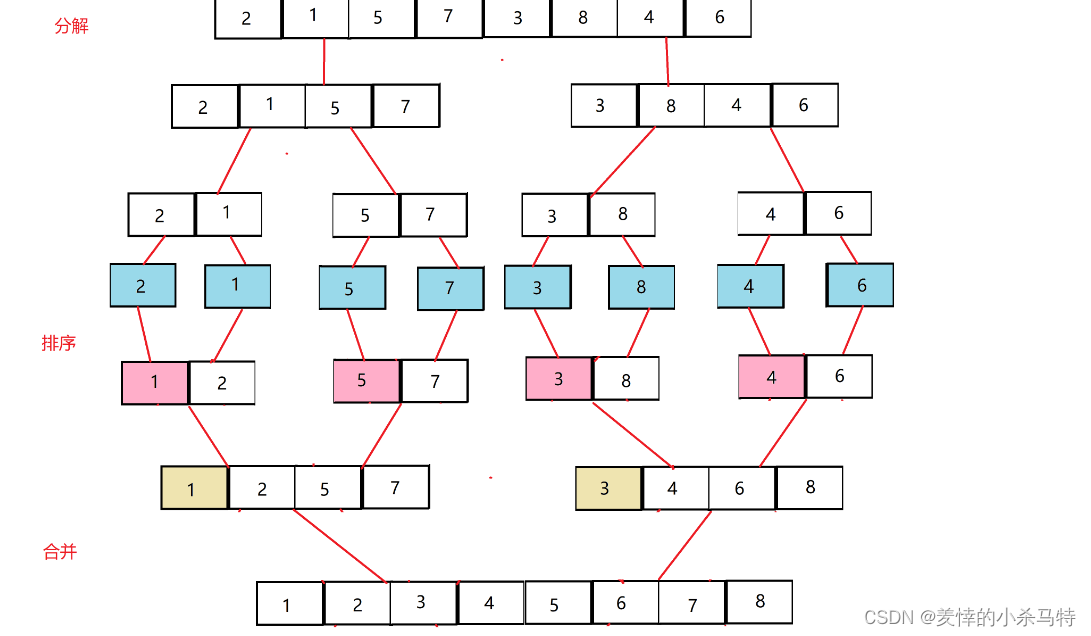
 首先，归并排序可以理解为用分治策略的一种排序算法，这里可以用递归的思想去理解，对一个数组进行不断分割，每次分为两个子数组，直到最后剩下的是一个数据也就是不可再分割，那么就开始对末两个子数组进行归并，然后归回去，在原数组得到有序的数组。（也就是说再每次归并的两个数组一定要是有序的）。

二·归并排序递归版本：

2.1·递归思路：

实现代码的同时，首先要先分割原数组为两个子数组，这里就用到了分割方法，分割的区间为[left，mid][mid+1，right]这样分割，可以避免出现区间循环的问题（[偶数，偶数+1]）。

(注：其它细节见代码处注释)

2.2·递归代码实现：

//归并的时候要确保每两个区间内数据都是有序的
//这里可以是递归，但是不让它每次都开辟空间，故这里用了一个子函数来完成递归操作

//这里可以假设完成的是最后一次归并操作，通过调用两次子函数假设已经把最后两个区间排好序了，最后
//再对它们归并即可。
void _mergesort(int* a, int* tmp, int begin, int end) {
	if (begin >= end) {
		return;
	}//递归终止条件：多为不断分割区间到只剩下一个数据结束直接归并
	int mid = (begin + end) / 2;
	_mergesort(a, tmp, begin, mid);//这里由于如果选mid-1和mid的话，当区间为【偶数，偶数+1】就会分割死循环
	_mergesort(a, tmp, mid + 1, end);
	int begin1 = begin;
	int begin2 = mid + 1;
	int end1 = mid;
	int end2 = end;
	//由于每次归并都是从原数组归到tmp，而最后又要把tmp对应的位置数据copy回原数组，故当我们归并排序到tmp数组
	//应对应原数组下标放入
	int i = begin;
	while (begin1 <= end1 && begin2 <= end2) {
		if (a[begin1] < a[begin2]) {
			tmp[i++] = a[begin1++];
		}
		else {
			tmp[i++] = a[begin2++];
		}
	}
	if (begin1 > end1) {
		while (begin2 <= end2) {
			tmp[i++] = a[begin2++];
		}
	}
	else {
		while (begin1 <= end1) {
			tmp[i++] = a[begin1++];
		}
	}
	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
	//这里开辟的tmp数组，可防止原数组被覆盖，每次归并完为有序的数组copy回原数组原位置

}
//这里递归每次分割，最后成一个数据自然有序，接着每次归并后归回去。
void mergesort(int* a, int n) {
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL) {
		perror(malloc);
		return;
	}
	_mergesort(a, tmp, 0, n - 1);
	free(tmp);
	tmp = NULL;
}

三·归并排序非递归版本：

3.1·非递归思路：

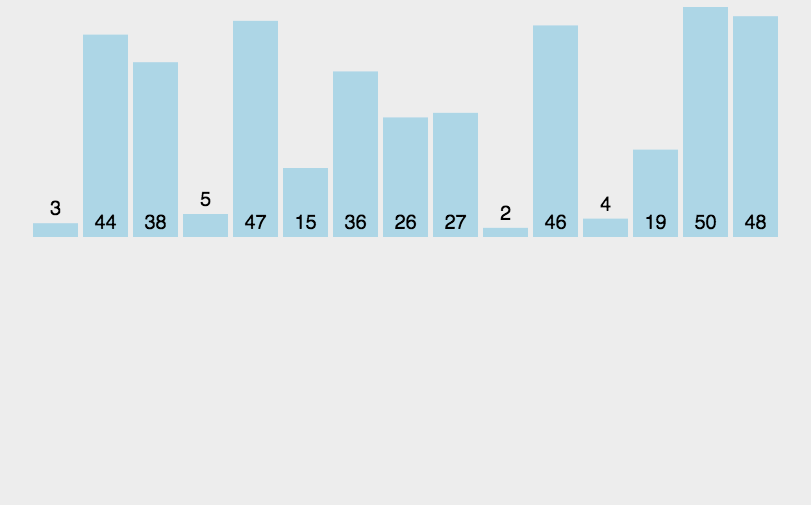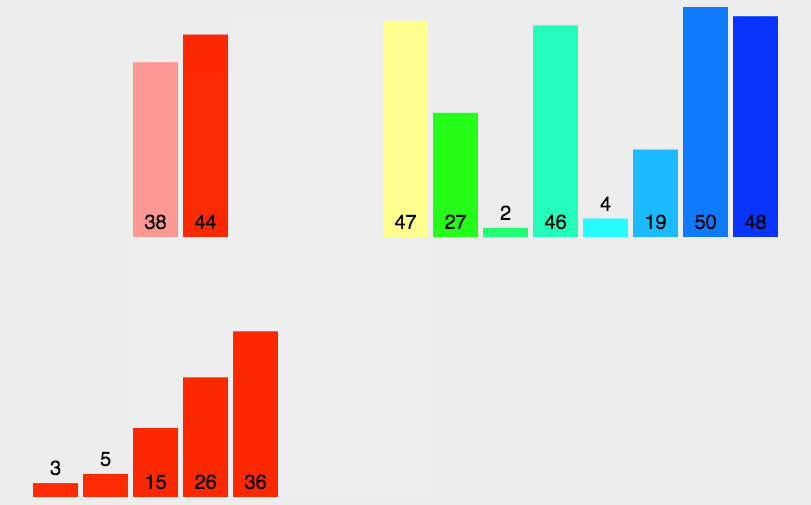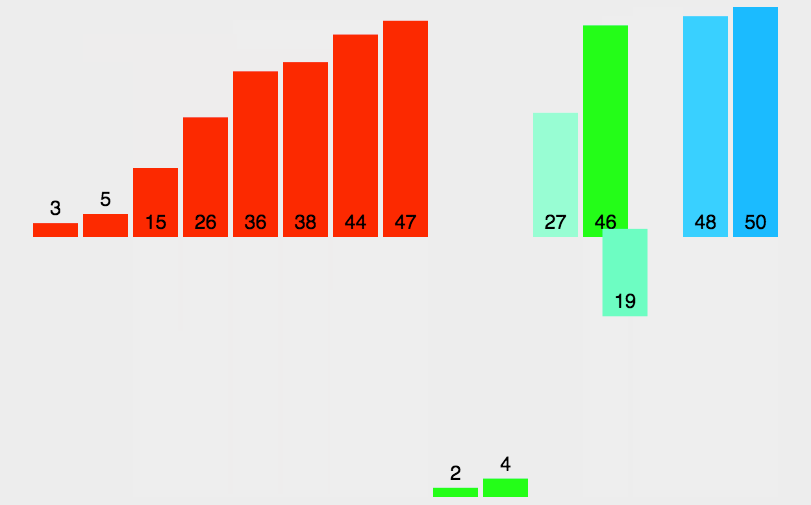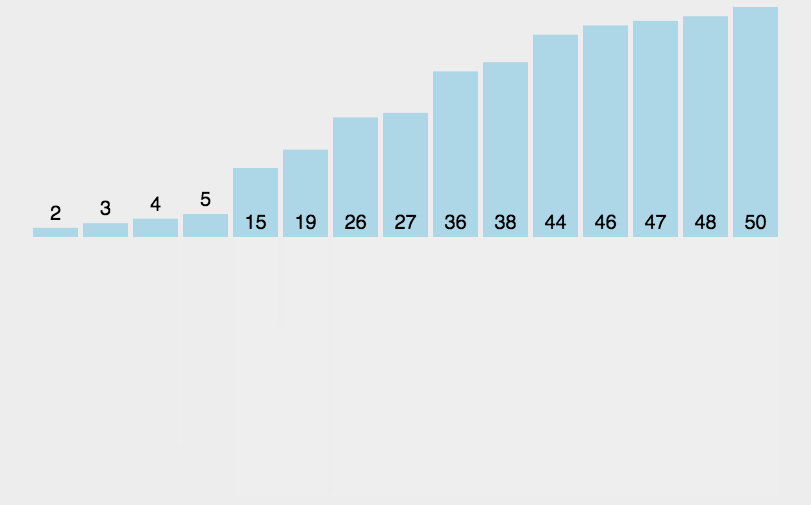
上面这个非递归的归并排序，是先是gap=1，归并当出现gap可以=2的时候再整体归并，这时整个数组并未被gap=1遍历完分好组，也是可以的，下面介绍一种直接被gap遍历完分好组再进行归并的方法：

非递归的话，就是把数组先分为一个个的每个子区间只有一个数据，然后让它们每两个成一对进行归并操作，等这一轮进行完后，从数组首开始给它们两个数据为一个区间，每两个区间就会满足区间内数据均有序，从而再次进行归并操作，依次类推，最后会生成两组有序归并完后得到原数组即为有序的原数组。

这里用gap来记录每组数据个数，通过循环来改变gap，gap定值时候用for循环来确定每次分两组情况。

而这里需要考虑的重点就是越界问题，当分区间的时候无论奇数个还是偶数个数据都会存在越界现象，而如果为奇数个的话，当gap为1的时候，最后会存在越界，而偶数的时候，可能往后面才出现越界，而画图可知道，由于每次第一组的区间首位是i不会越界故越界的是第二组要么是都越界，要么第二个区间的第二个数字越界。（其他细节见源代码注释）

画图解释：

3.2·非递归代码实现：

//这里非递归，可以从每组一个数据开始归并，然后有序，然后每两个就有序了，
// 最后会变为最后的两组要么归并要么舍弃一组
// 接着每组两个归并成四个，依次每组gap个数据调整到最后剩下两组，即再次归并得到最后有序的数组
//画图可知道每次如果出现越界只能是最后两组，而这两组的第一组的end1为i不可能越界
//故可以分数据为偶数个还是奇数个，如果偶数个那么gap为1时不越界但是之后会，为奇数时gap为1最后一组
//越界，然后出现越界肯定是第二组，然后begin2如果越，就break，而end2越界就变为n-1接着归并
//可发现gap跳的时候每次都是跳的2的多少次方，即当剩下的组区间有越界但里面有数据一定是有序的，变为n-1归并
void  mergesortNoR(int* a, int n) {
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL) {
		perror(malloc);
		return;
	}

	for (int gap = 1; gap < n; gap = 2 * gap) {
		for (int i = 0; i < n; i += 2 * gap) {
			//两边闭区间
			int begin1 = i;
			int end1 = i + gap - 1;
			int begin2 = i + gap;
			int end2 = i + 2 * gap - 1;
			if (begin2 >= n) {
				break;
				//由于最后两组如果出现越界的话end1始终不会越界，一旦越界begin2一定越界
				//那么就防止后面的归并出错，就停止归并
			}
			if (end2 >= n) {
				end2 = n - 1;
				//当最后一次gap+的循环，肯定第二组begin2不越界，越界可能是end2，而前几次的归并
				//已经把最后一次第二组的数据排好序了那么更改end2然后再次归并就可以了
			}
			int i = begin1;
			int start = begin1;
			int last = end2;
			while (begin1 <= end1 && begin2 <= end2) {
				if (a[begin1] < a[begin2]) {
					tmp[i++] = a[begin1++];
				}
				else {
					tmp[i++] = a[begin2++];
				}
			}
			if (begin1 > end1) {
				while (begin2 <= end2) {
					tmp[i++] = a[begin2++];
				}
			}
			else {
				while (begin1 <= end1) {
					tmp[i++] = a[begin1++];
				}
			}
			memcpy(a + start, tmp + start, sizeof(int) * (last - start + 1));


		}
	}

}

四·归并排序性能分析：

复杂度：首先由于归并排序每次是折半归，故它的时间复杂度类似于二叉树为o（n*logn）,而由于多开了n个空间的数组作为归并暂存数组用来copy。空间复杂度为：o（n）。

稳定性：首先稳定性就是当用排序算法给数组排序的时候，它里面原本的相同的元素相对位置不变化就称为其的稳定性。对于归并排序而言，每次两个数组归并成一个数组，只要我们改动一下当begin1与begin2对应数字相等，就放入begin1对应的数据，这样顺序就不变了，也可以说归并排序是稳定的。

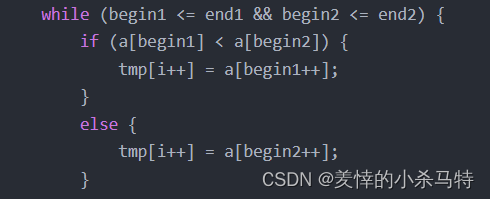
就是把<改成=。

应用：可用于正常的排序，或者大文件的排序，由于归并排序是在内存中进行，有的时候文件太大无法正常进行，可以把它分为一个个小文件到内存归为有序，最终整合使得大文件也有序。