一、选题背景
以多元线性回归统计模型为基础,用R语言对美国部分地区房价数据进行建模预测,进而探究提高多元回 归线性模型精度的方法。先对数据进行探索性预处理,随后设置虚拟变量并建模得出预测结果,再使用方差膨胀因子对 多重共线性进行修正,从而提高模型精度与稳健性,使回归结果在很大程度上得到优化。...
近年来,随着经济的不断增长,飞速增长的房价仍然是民众心中最看重的问题之一。房地产行业是我国经济健康发展的稳定器,也是加快我国经济增长的助力器,不仅对经济社会起着重要的支撑作用,还对社会的稳定产生着难以衡量的影响。
二、文献综述
...
三、方案论证(设计理念)
多元线性回归具有非常广泛的应用范围,但在实 际预测中对存在类别变量设置不充分或多重共线性 问题,导致统计模型缺乏精度和稳健性。由此,本文对如何精准且高效的排除多重共线性影响,并合理地 将分类变量转化为虚拟变量,提升多元线性回归模型 精度作了进一步探索,并将其应用于房价预测上。
四、实证分析
在美国房屋信息数据集中,包含不同地区的平均房价及多个可能影响房价的自变量:AvgAreaIncome(该地区的平均收入) AvgAreaHouseAge (房子的平均面积)AreaPopulation(该地区的人口数量)等。首先进行数据展示
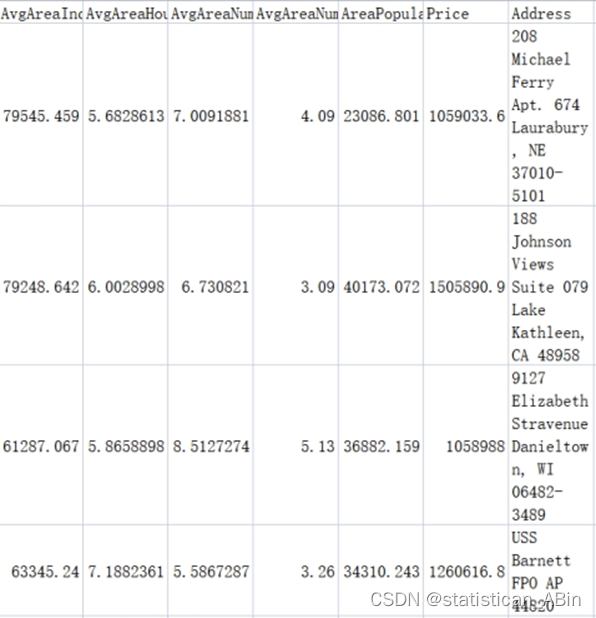
随后读取数据并且进行描述性统计
library(openxlsx)
# 文件名+sheet的序号
dataset<- read.xlsx("house.xlsx", sheet = 1)
#View(dataset)
dataset
summary(dataset)#####描述性统计分析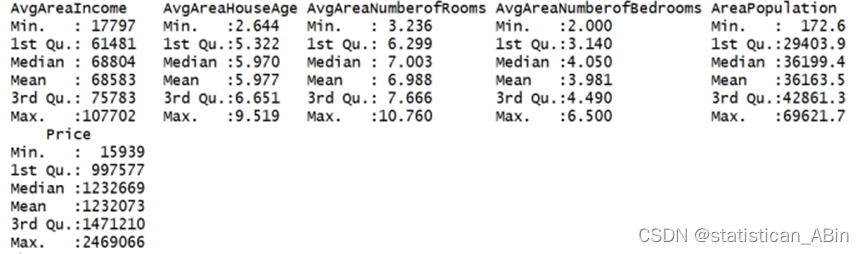
具体描述性统计如上,包括各个变量的最大值、最小值、中位数、1/4分位数和3/4分位数等
接下来画出价格、该地区的平均收入的柱状图查看情况:


###画出price柱状图
price<-dataset$Price
price
head(price,n=100)
barplot(head(price,n=100),xlab="house",ylab="prcie",col="blue",main="房价柱状图(前100个)",border="red")
####画出该地区的平均收入柱状图
income<-dataset$AvgAreaIncome
income
head(income,n=100)
barplot(head(income,n=100),xlab="",ylab="收入",col="pink",main="该地区的平均收入柱状图(前100个)",border="green")画出特征变量的箱线图,看其分布形状,如图所示:

由图可得,6个特征变量均分布较好且,存在异常值但是异常值很少。
接下来运用热力图展示出特征变量与响应变量的关系图:

从相关系数热力图可以看出,几乎每个特征变量对房价的相关系数都较高,但是其中该地区的平均收入与房价的相关系数是最高的,为0.64。
再用ggpairs函数展示出变量间的相关性,以及从下图中的相关系数中也可得出其相关性。

接下来用房价对最初的特征变量进行回归,结果如下:
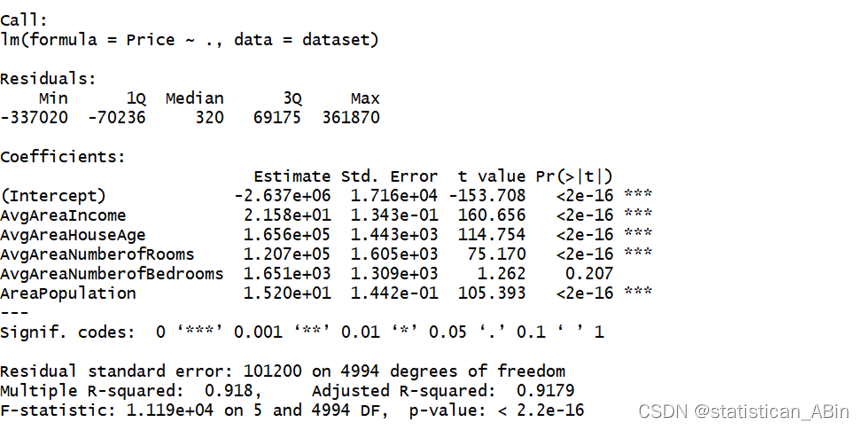
图为软件R计算的结果。R²反应了全部6个x与y之间的线性相关水平。其中调整后的拟合优度为0.9179,接近于1,表明该模型对数据的拟合程度比较好,并且可以说明Price的91.79%可由这些因素来解释。P值<0.01,说明p的值非常的小,表明有99%的把握认为至少有一个解释变量是属于这个回归方程的,但这只能说明模型总体是显著的,且*号越多影响越显著。
运用向后逐步回归,每次计算AIC值不断剔除一个变量,利用其余变量进行回归,最终方程为:
 接下来进行模型检验
接下来进行模型检验
表 1 异方差检验结果
| Stufentsized Breusch-Pagan test |
| Data: fit1 |
| BP= 10.385, df=4 , p_value=0.03441 |
由于p值小于0.05,拒绝原假设,可认为该模型不存在异方差性。
接下来,画出回归值与残差的残差图

五、结论
本次实验完整的研究了多元线性回归模型,首先简单的介绍了多元线性回归模型及其相关的基本理论,然后运用 R 语言实现多元回归模型的拟合,学习了如何求变量间的相关系数矩阵和画散点图矩阵,然后运用 lm 函数拟合回归模型,并运用赤池信息准则选择最优模型,最终对拟合的最优模型进行预测。
代码加数据
代码加数据加报告
创作不易,希望大家多多点赞收藏和评论!