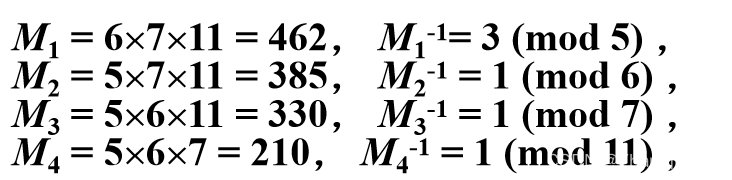6.1 剩余系(掌握)
6.2 同余式概念与一次同余式(熟练)
6.3 中国剩余定理(熟练)
6.1 剩余系
设m是正整数,模m同余的全体整数是一个模m剩余类,即可表示为a = qm+r, 0≤r<m,q=0,±1,±2,…, 的整数是一个模m剩余类。
剩余类中的每个数都称为该类的代表
r称为该类的最小非负剩余
模m剩余类共有m个
例:全部模8的剩余类为
{0,±8,±2×8,±3×8,…},
{1,1±8,1±2×8,1±3×8,…},{2,2±8,2±2×8,2±3×8,…},
…
{7,7±8,7±2×8,7±3×8,…}.
在数轴上,一个剩余类做任意整数间隔的平移仍然是一个剩余类,或是另一个剩余类,或是它自己。
定义:从模m剩余类中各取一个代表,则称这些代表的集合为模m的一个完全剩余系。
显然一个完全剩余系在数轴上的任意整数间隔的平移都是一个完全剩余系:
定理:设a是一个整数且(a,m) =1,b是任意整数.如果x遍历模m的一个完全剩余系,则ax+b也遍历模m的完全剩余系。
即如果![]() 是模m的一个完全剩余系,则
是模m的一个完全剩余系,则![]() 也是模m的完全剩余系。
也是模m的完全剩余系。
定理:如果x1,x2分别遍历模m1和模m2的完全剩余系,且(m1,m2) = 1,则m2x1+m1x2遍历模m1m2的完全剩余系。
定义:如果一个模m的剩余类里面的数与m互素,则称它为与模m互素的剩余类。从与模m互素的每个剩余类中各取一个数构成的集合称为模m的一个简化剩余系。
推论:如果m1,m2是两个正整数,且(m1,m2)=1,则φ(m1m2)=φ(m1)φ(m2)。
定理:设正整数m的标准分解式为![]() 则
则![]() 。
。
定理:模m剩余类环中与m互素的剩余类构成乘法群。
推论:设m是正整数,如果(r,m) =1,则存在s使sr=1 (mod m),反之也成立。 换句话说,就是如果r,m互素,则r在模m下必存在逆元s。
推论(欧拉定理):设m是正整数,如果(r,m) =1,则r^φ( m)≡1(mod m)
推论(费马定理):如果p是素数,则r^p≡r (mod p)
6.2 同余式概念与一次同余式
定义:设f(x)为多项式:![]() 其中n是正整数,ai (0≤i≤n)是整数,则
其中n是正整数,ai (0≤i≤n)是整数,则![]() 称为模m的同余式.如果an≠0 (mod m),则n称为同余式的次数。如果x0满足
称为模m的同余式.如果an≠0 (mod m),则n称为同余式的次数。如果x0满足![]() 则x≡x0 (mod m)称为同余式的解.不同的解指互不同余的解.
则x≡x0 (mod m)称为同余式的解.不同的解指互不同余的解.
例:求下列同余式的解.
1)
解 x≡1,5,6 (mod 7)
2)
解 x≡1,3,5,7,9,11,13,15 (mod 16)
3)
解 无解.
一次同余式
定理:一次同余式ax ≡ b (mod m),a≠0 (mod m),有解的充分必要条件为(a,m)|b.
例:求980x ≡ 1500 (mod 1600)的解.
解 此题中,a = 980,m = 1600,b = 1500,(a,m) = 20,a’ = 49,m’= 80。
1)首先采用欧几里得算法求a’^(-1)(mod m’)。 由于(a’,m’) = 1,所以存在r,s,使a’r+ m’s = 1
于是我们有 31 = 80 – 49= m’ -a’,18 = a’ – 31 = 2a’ – m’,13 = 31 – 18 = 2m’ – 3a’ ,5 = 18 – 13 = 5a’ – 3m’ ,3 = 13 – 2×5 = 8m’ – 13a’ ,2 = 5 – 3 = 18a’ – 11m’ , 1 = 3 – 2 = 19m’ – 31a’ 。
所以19m’ – 31a’ = 1,
则– 31a’ ≡ 49a’ ≡ 1 (mod 80)
故a’^(-1) = 49.
2)求x0
3)同余式的解共有20个,它们为
x ≡ 75+80k (mod 1600),k = 0,1,…,19.
6.3 中国剩余定理
定理(中国剩余定理):设m1,m2,…,mk两两互素,则右边的同余式组有解,且有 唯一解:
唯一解:![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,i =1,2,…,k。
,i =1,2,…,k。
例:解同余式组:
x ≡ 1 (mod 5)
x ≡ 5 (mod 6)
x ≡ 4 (mod 7)
x ≡ 10 (mod 11)
按中国剩余定理求解如下: m = 5×6×7×11 = 2310,
x ≡ 3×462 + 385×5 + 330×4 + 210×10 ≡ 6731 ≡ 2111 (mod 2310).