题目描述
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1
输出:[1]
提示:
1 <= nums.length <= 10^5
-104 <= nums[i] <= 10^4
1 <= k <= nums.length
以下参考力扣官方题解:
链接:https://leetcode.cn/problems/sliding-window-maximum/solutions/543426/hua-dong-chuang-kou-zui-da-zhi-by-leetco-ki6m/
相关标签
队列、滑动窗口、单调队列、堆(优先队列)
解题思路
对于每个滑动窗口,可以使用
O
(
k
)
O(k)
O(k)的时间遍历每个元素,找到最大值。对于长度为 n 的数组 nums,窗口的数量为 n-k+1,因此算法的时间复杂度为
O
(
(
n
−
k
+
1
)
k
)
=
O
(
n
k
)
O((n-k+1)k)=O(nk)
O((n−k+1)k)=O(nk),会超出时间限制,需要进行一些优化。可以想到,对于两个相邻(只差一个位置)的滑动窗口,共用着 k-1 个元素,只有一个元素是变化的,可以根据这个特点进行优化。
解法1:优先队列
对于最大值,可以想到一种非常合适的数据结构,优先队列(堆),其中的大根堆可以帮助我们实时维护一系列元素中的最大值。
初始时,将数组的前k个元素放入优先队列中。每当向右移动窗口时,可以把一个新的元素放入优先队列中,此时堆顶的元素就是堆中所有元素的最大值。然而这个最大值可能不在滑动窗口中,而是出现在滑动窗口左边界的左侧。因此当我们继续向右移动窗口时这个值就永远不可能出现在滑动窗口中了,我们可以将其从优先队列中删除。
我们不断地移除堆顶元素,直到其确实出现在滑动窗口中。此时,堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素和滑动窗口的位置关系,我们可以在有限队列中存储二元组
(
n
u
m
,
i
n
d
e
x
)
(num, index)
(num,index),表示元素 num 在数组中的下标为 index。
code
class Solution:
def maxSlidingWindow(self, nums:List[int], k:int) -> List[int]:
n = len(nums)
# python 默认的优先队列是小根堆
q = [(-nums[i], i) for i in range(k)]
heapq.heapify(q)
ans = [-q[0][0]]
for i in range(k, n):
heapq.heappush(q, (-nums[i], i))
while q[0][1] <= i-k:
heapq.heappop(q)
ans.append(-q[0][0])
return ans
Python的heapq库是用于实现堆(优先队列)算法的库。它提供了一些函数来操作堆结构,如push、pop、heapify等。
heapq.heapify(q):将列表heap原地转换为一个堆。
heapq.heappush(heap, item:将元素item推入堆heap上。
heapq.heappop(q):从堆heap中弹出并返回最小的元素。
复杂度分析:
- 时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn),其中n数数组 nums 的长度。在最坏情况下数组的元素单调递增,那么最终优先队列中包含了所有元素,没有元素被移除。由于将一个元素放入优先队列的时间复杂度为 O ( n ) O(n) O(n),因此总时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)。
- 空间复杂度: O ( n ) O(n) O(n),即优先队列需要使用的空间。这里所有的空间复杂度分析都不考虑返回的答案需要的空间,只计算额外的空间使用。
解法2:单调队列
由于我们需要求出的是滑动窗口的最大值,如果当前的滑动窗口中有两个下标i 和j,其中i 在 j的坐标,并且i 对应的元素不大于 j 对应的元素。那么当滑动窗口向右移动时,只要i 还在窗口中,那么j 一定也还在窗口中。因此i对应的元素一定不会是窗口中的最大值了,可以将其永久移除。
因此可以使用一个队列存储所有还没有被移除的下标,在队列中这些下标按照从小到大的顺序被存储,并且在数组nums中对应的值是严格单调递减的。
当窗口向右移动时,为了保持队列的性质,会不断将新的元素和队尾的元素相比较,如果前者大于等于后者,那么队尾的元素就可以被永久移除,弹出队列。不断进行此操作,知道队列为空或新元素小于队尾元素。
由于队列中下标对应的元素是严格单减的,因此队首下标对应的元素就是滑动窗口中的最大值。此时最大值可能在窗口左边界的左侧,因此还需要不断从队首弹出元素,直到队首元素在窗口中。
为了科研同时弹出队首和队尾的元素,需要使用双端队列。满足这种单调性的双端队列一般称为单调队列。
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
n = len(nums)
q = collections.deque()
for i in range(k):
while q and nums[i] >= nums[q[-1]]:
q.pop()
q.append(i)
ans = [nums[q[0]]]
for i in range(k, n):
while q and nums[i] >= nums[q[-1]]:
q.pop()
q.append(i)
while q[0] <= i - k:
q.popleft()
ans.append(nums[q[0]])
return ans
复杂度分析
- 时间复杂度: O ( n ) O(n) O(n)。每个下标恰好被放入队列一次,并且最多被弹出队列一次。
- 空间复杂度:这里使用的数据结构是双向的,因此不断从队首弹出元素保证了队列中最多不会有超过 k+1 个元素,因此队列使用的空间为 O ( k ) O(k) O(k)。
解法3: 分块 + 预处理
可以将数组nums从左到右按照k个一组进行分组,最后一组中元素的数量可能会不足k个。如果希望求出nums[i]到nums[i+k-1]的最大值就会有两种情况:
- 如果 i 是 k 的倍数,那么 nums[i] 到 nums[i+k-1] 恰好是一个分组。只要预处理出每个分组中的最大值即可;
- 如果 i 不是 k 的备注,那么会跨越两个分组,占有第一个分组的后缀以及第二个分组的前缀。假设 j 是 k 的倍数,并且 i < j <= j+k-1,那么 nums[i]~nums[j-1]就是第一个分组的后缀,nums[j] 到 nums[i+k-1] 就是第二个分组的前缀。如果预处理出每个分组中的前缀最大值和后缀最大值,也可以在 O(1) 的时间得到答案。
用 prefixMax [ I ] \textit{prefixMax}[I] prefixMax[I]表示下标 i 对应的分组中,以 i 结尾的前缀最大值; suffixMax [ i ] \textit{suffixMax}[i] suffixMax[i] 表示下标 i 对应的分组中,以 i 开始的后缀最大值。它们分别满足如下的递推式
prefixMax [ i ] = { nums [ i ] , i 是 k 的倍数 max { prefixMax [ i − 1 ] , nums [ i ] } , i 不是 k 的倍数 \textit{prefixMax}[i]=\begin{cases} \textit{nums}[i], & \quad i ~是~ k ~的倍数 \\ \max\{ \textit{prefixMax}[i-1], \textit{nums}[i] \}, & \quad i ~不是~ k ~的倍数 \end{cases} prefixMax[i]={nums[i],max{prefixMax[i−1],nums[i]},i 是 k 的倍数i 不是 k 的倍数
以及
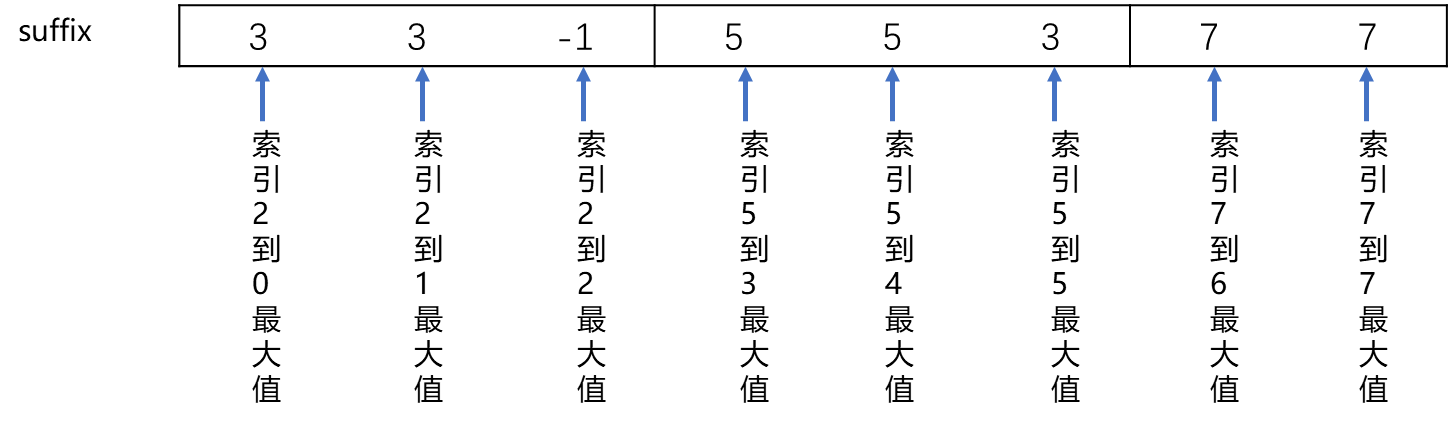
suffixMax [ i ] = { nums [ i ] , i + 1 是 k 的倍数 max { suffixMax [ i + 1 ] , nums [ i ] } , i + 1 不是 k 的倍数 \textit{suffixMax}[i]=\begin{cases} \textit{nums}[i], & \quad i+1 ~是~ k ~的倍数 \\ \max\{ \textit{suffixMax}[i+1], \textit{nums}[i] \}, & \quad i+1 ~不是~ k ~的倍数 \end{cases} suffixMax[i]={nums[i],max{suffixMax[i+1],nums[i]},i+1 是 k 的倍数i+1 不是 k 的倍数
需要注意在递推 suffixMax [ i ] \textit{suffixMax}[i] suffixMax[i] 时需要考虑到边界条件 suffixMax [ n − 1 ] = nums [ n − 1 ] \textit{suffixMax}[n-1]=\textit{nums}[n-1] suffixMax[n−1]=nums[n−1],而在递推 prefixMax [ I ] \textit{prefixMax}[I] prefixMax[I] 时的边界条件 prefixMax [ 0 ] = nums [ 0 ] \textit{prefixMax}[0]=\textit{nums}[0] prefixMax[0]=nums[0] 恰好包含在递推式的第一种情况中,因此无需特殊考虑。
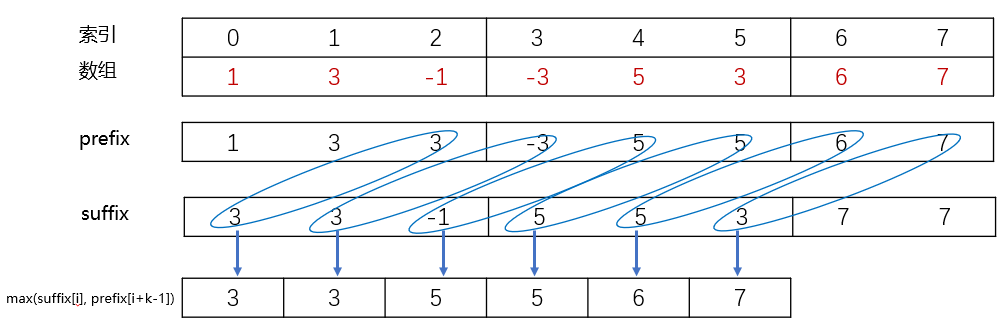
在预处理完成之后,对于 nums [ I ] \textit{nums}[I] nums[I]到 nums [ i + k − 1 ] \textit{nums}[i+k-1] nums[i+k−1] 的所有元素,如果 i 不是 k 的倍数,那么窗口中的最大值为 suffixMax [ I ] \textit{suffixMax}[I] suffixMax[I] 与 prefixMax [ i + k − 1 ] \textit{prefixMax}[i+k-1] prefixMax[i+k−1] 中的较大值;如果 i 是 k 的倍数,那么此时窗口恰好对应一整个分组, suffixMax [ I ] \textit{suffixMax}[I] suffixMax[I] 和 prefixMax [ i + k − 1 ] \textit{prefixMax}[i+k-1] prefixMax[i+k−1] 都等于分组中的最大值,因此无论窗口属于哪一种情况,
suffixMax [ i ] , prefixMax [ i + k − 1 ] } \textit{suffixMax}[i], \textit{prefixMax}[i+k-1] \big\} suffixMax[i],prefixMax[i+k−1]}即为答案。
此方法和稀疏表(Sparse Table)很类似。
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
n = len(nums)
prefixMax, suffixMax = [0] * n, [0] * n
for i in range(n):
if i % k == 0:
prefixMax[i] = nums[i]
else:
prefixMax[i] = max(prefixMax[i - 1], nums[i])
for i in range(n - 1, -1, -1):
if i == n - 1 or (i + 1) % k == 0:
suffixMax[i] = nums[i]
else:
suffixMax[i] = max(suffixMax[i + 1], nums[i])
ans = [max(suffixMax[i], prefixMax[i + k - 1]) for i in range(n - k + 1)]
return ans
复杂度分析
- 时间复杂度:O(n);
- 空间复杂度:存储prefixMax和suffixMax需要的空间。
评论区一个很好的示例: