目录
- 1. motivation
- 2. overall
- 3. model
- 3.1 low rank parametrized update matrices
- 3.2 applying lora to transformer
- 4. limitation
- 5. experiment
- 6. 代码
- 参考文献
1. motivation
- 常规的adaptation需要的微调成本过大
- 现有方法的不足:
- Adapter Layers Introduce Inference Latency
- Directly Optimizing the Prompt is Hard
2. overall
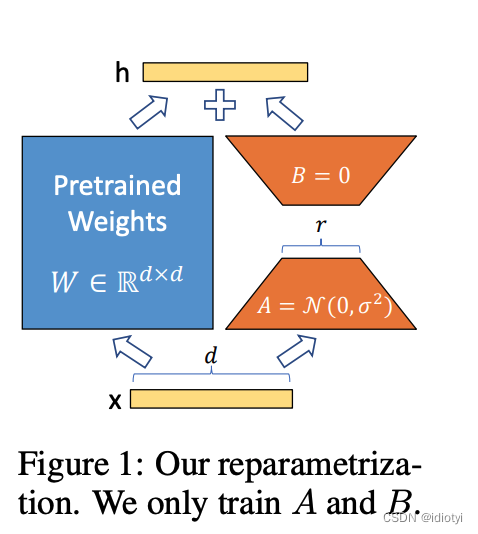
- inspiration
Aghajanyan[1] 证明了预训练语言模型有一个低的“intrinsic rank”,并且将其映射到一个子空间后仍然可以有效率的学习 - hypothesis
假设模型自适应过程中,权重的改变也具有一个低的“intrinsic rank” - core idea
通过优化全连接层改变量的秩分解矩阵去微调全连接层
3. model
3.1 low rank parametrized update matrices
采用秩分解矩阵代表权重的改变量:
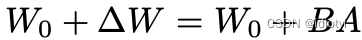
则对于任意的输出:
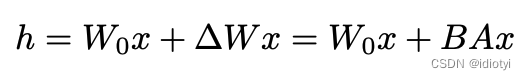
A
∈
R
d
×
r
,
B
∈
R
r
×
d
,
r
<
<
d
{A\in R^{d \times r}}, {B \in R^{r \times d}}, r<<d
A∈Rd×r,B∈Rr×d,r<<d
对于A采用一个随机的高斯初始化,对于B采用0初始化。
采用
α
/
r
{\alpha/r}
α/r缩放
δ
W
x
{\delta Wx}
δWx,r是矩阵的秩,
α
{\alpha}
α是一个常数。这个缩放可以减小当r改变时,我们重新微调参数的需要
A generalization of full fine-tune
adapter-based的方法通常是利用一个MLP或者一个prefix-based方法,导致模型不允许长序列的输入。不同于adapter-based的方法,LORA是针对原始模型训练的。LORA微调时,我们可以通过设置r来达到恢复全量微调的效果。因为LORA在适应过程中不要求对权重矩阵的累积梯度更新具有完整的秩。
no additional inference latency
部署到实际生产时,可以先计算存储
W
=
W
0
+
B
A
{W = W_0 + BA}
W=W0+BA。对于不同的下游任务,只用计算BA和其变化量的差值就可以了。
3.2 applying lora to transformer
- transformer的框架中,有四个权重矩阵在自注意力层( W q , W k , W v , W o {W_q,W_k, W_v, W_o} Wq,Wk,Wv,Wo),两个在MLP。
- lora微调时只针对四个自注意力层的矩阵,冻结MLP的两个矩阵(即下游任务不训练)。
4. limitation
For example, it is not straightforward to batch inputs to different tasks with different A and B in a single forward pass, if one chooses to absorb A and B into W to eliminate additional inference latency. Though it is possible to not merge the weights and dynamically choose the LoRA modules to use for samples in a batch for scenarios where latency is not critical.
5. experiment
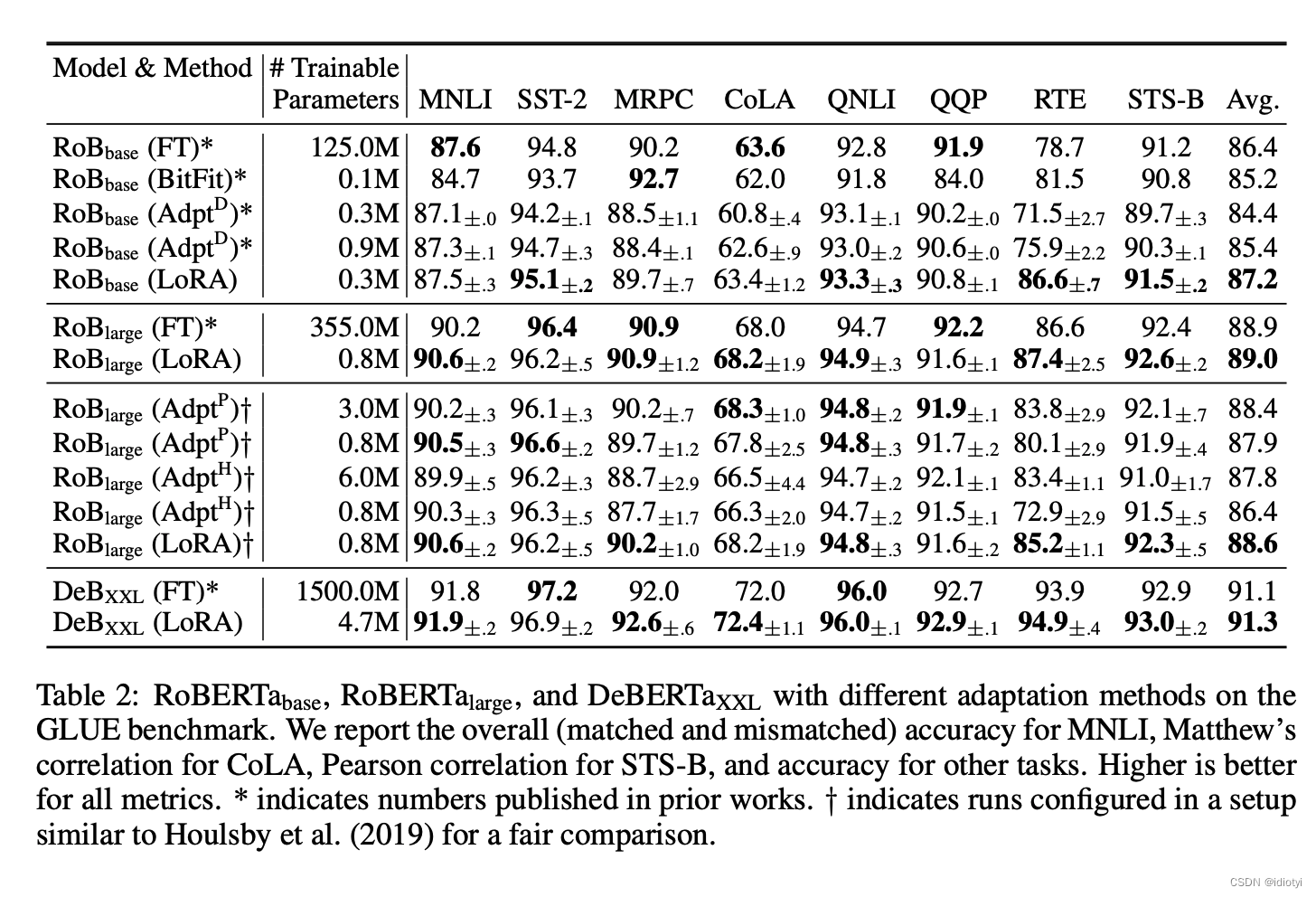
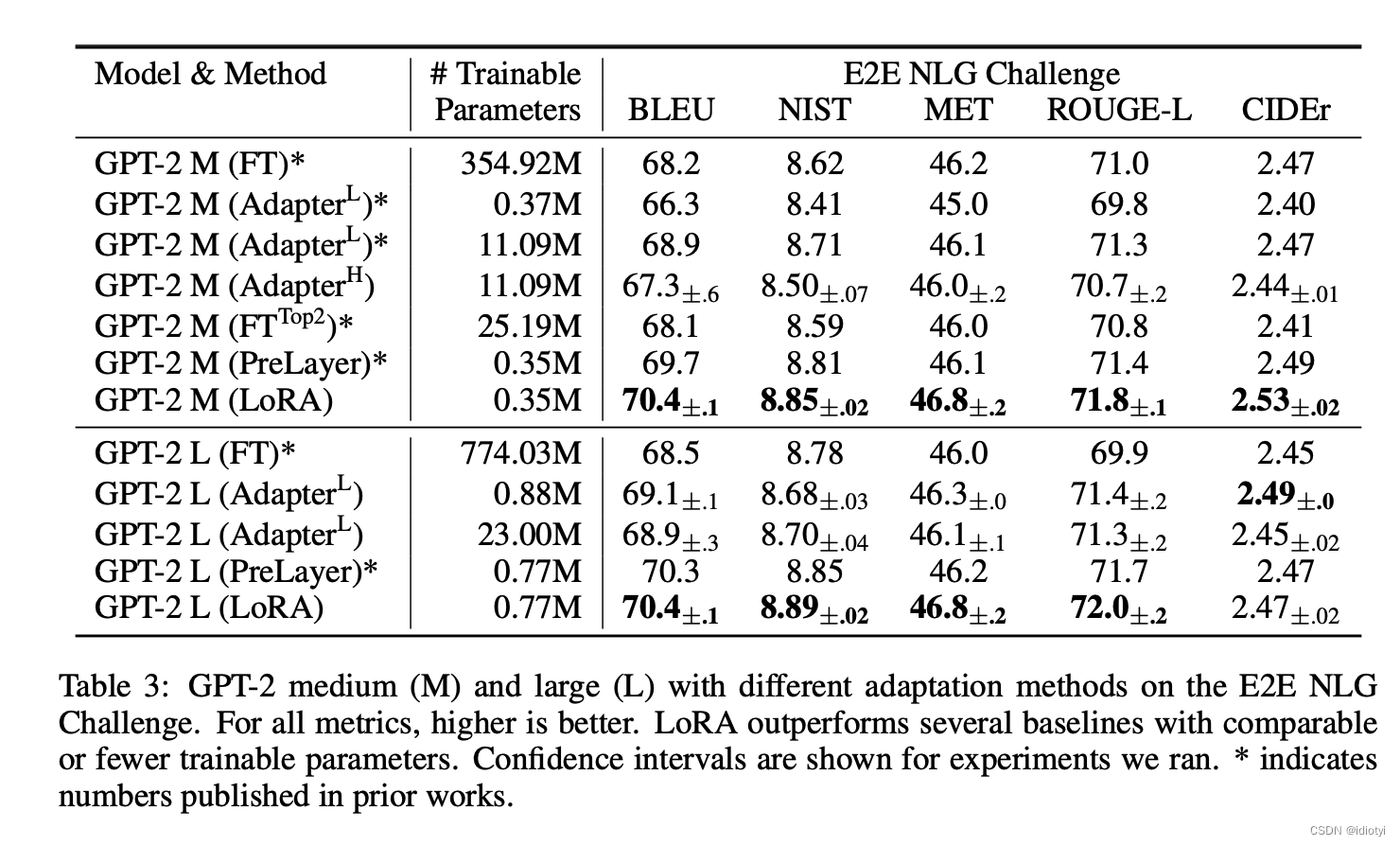
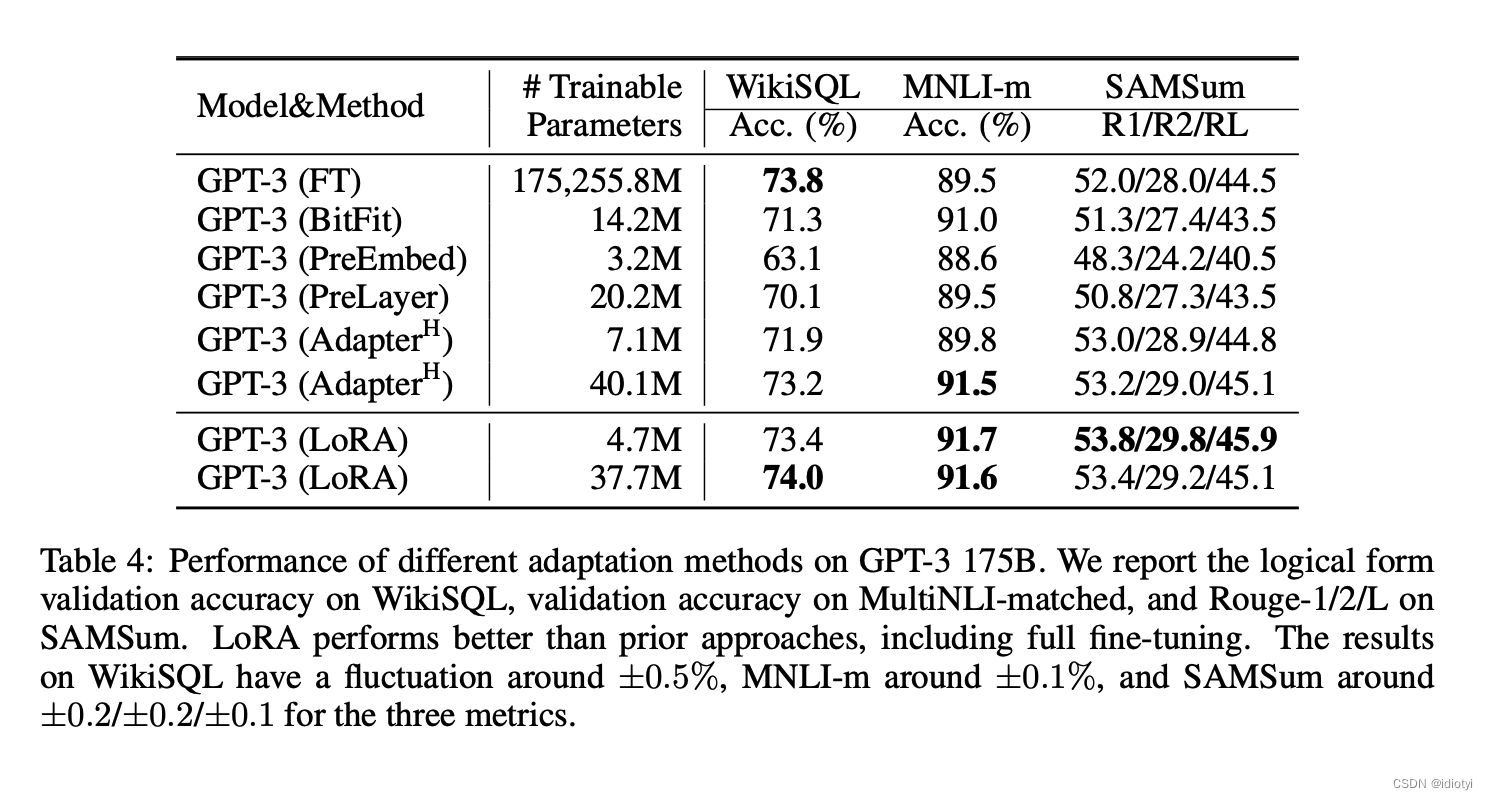
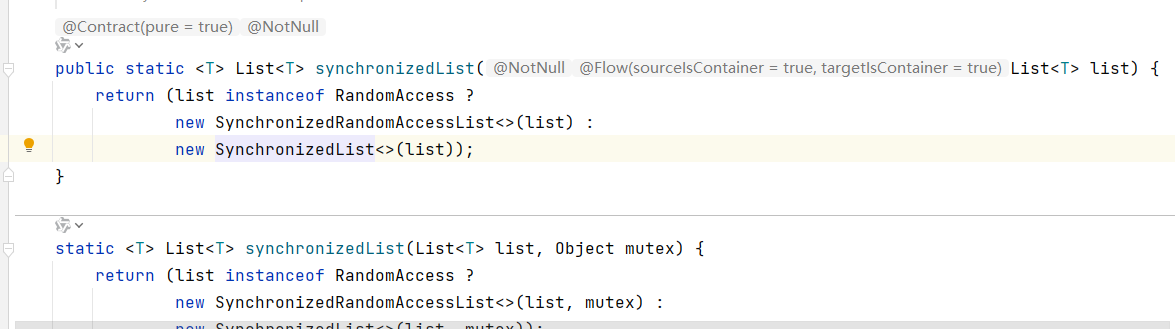
6. 代码
- lora层

- 普通的前馈网络

- 加入lora后

参考文献
[1] Armen Aghajanyan, Luke Zettlemoyer, and Sonal Gupta. Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning. arXiv:2012.13255 [cs], December 2020. URL
http://arxiv.org/abs/2012.13255.
[2]大模型微调原理与代码实战案例(四):LoRA


![[职场] 生活管家的工作要求 #其他#职场发展](https://img-blog.csdnimg.cn/img_convert/64b42dc9da5b75f35d5424393ef81e28.jpeg)