【代码随想录】【算法训练营】【第27天】 [39]组合总和 [40] 组合总和II [131]分割回文串

前言

思路及算法思维，指路代码随想录。
题目来自 LeetCode。

day26，休息的周末~
day 27，周一，库存没了，哭死~

题目详情

[39] 组合总和

题目描述

39 组合总和

解题思路

前提：组合的子集问题，统一元素可以重复选取
思路：回溯 + 剪枝。
重点：剪枝的前提是数组已排序。

代码实现

C语言

回溯 + 未排序剪枝

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */

void backtracing(int* candidates, int candidatesSize, int target, int index, int *nums, int numsSize, int ***ans, int* returnSize, int** returnColumnSizes)
{
    // 退出条件
    if (0 == target)
    {
        *ans = (int **)realloc(*ans, sizeof(int *) * ((*returnSize) + 1));
        (*ans)[*returnSize] = (int *)malloc(sizeof(int) * (numsSize));
        for (int i = 0; i < numsSize; i++)
        {
            (*ans)[*returnSize][i] = nums[i];
        }
        *returnColumnSizes = (int *)realloc(*returnColumnSizes, sizeof(int) * ((*returnSize) + 1));
        (*returnColumnSizes)[*returnSize] = numsSize;
        (*returnSize)++;
        return ;
    }
    
    for (int j = index; j < candidatesSize; j++)
    {
        if (target < candidates[j])
        {
            continue ;
        }
        // 递归
        nums[numsSize] = candidates[j];
        numsSize++;
        backtracing(candidates, candidatesSize, target - candidates[j], j, nums, numsSize, ans, returnSize, returnColumnSizes);
        // 回溯
        numsSize--;
        nums[numsSize] = 0;
    }
    return ;
}

int** combinationSum(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes) {
    // 判空
    if (candidatesSize == 0)
    {
        return NULL;
    }
    // 输出
    int **ans = NULL;
    int nums[41];
    int index = 0;
    *returnSize = 0;
    printf("%d\n", target);
    backtracing(candidates, candidatesSize, target, 0, nums, 0, &ans, returnSize, returnColumnSizes);
    if (*returnSize == 0)
    {
        return NULL;
    }
    return ans;
}

回溯 + 排序 + 剪枝

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */

int cmp(const void *p1, const void *p2)
{
    return *(int *)p1 > *(int *)p2;
}

void backtracing(int* candidates, int candidatesSize, int target, int index, int *nums, int numsSize, int ***ans, int* returnSize, int** returnColumnSizes)
{
    // 退出条件
    if (0 == target)
    {
        *ans = (int **)realloc(*ans, sizeof(int *) * ((*returnSize) + 1));
        (*ans)[*returnSize] = (int *)malloc(sizeof(int) * (numsSize));
        for (int i = 0; i < numsSize; i++)
        {
            (*ans)[*returnSize][i] = nums[i];
        }
        *returnColumnSizes = (int *)realloc(*returnColumnSizes, sizeof(int) * ((*returnSize) + 1));
        (*returnColumnSizes)[*returnSize] = numsSize;
        (*returnSize)++;
        return ;
    }
    
    // 剪枝
    for (int j = index; (j < candidatesSize) && (target >= candidates[j]); j++)
    {
        // 递归
        nums[numsSize] = candidates[j];
        numsSize++;
        backtracing(candidates, candidatesSize, target - candidates[j], j, nums, numsSize, ans, returnSize, returnColumnSizes);
        // 回溯
        numsSize--;
        nums[numsSize] = 0;
    }
    return ;
}

int** combinationSum(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes) {
    // 判空
    if (candidatesSize == 0)
    {
        return NULL;
    }
    // 排序
    qsort(candidates, candidatesSize, sizeof(int), cmp);
    // 输出
    int **ans = NULL;
    int nums[41];
    int index = 0;
    *returnSize = 0;
    backtracing(candidates, candidatesSize, target, 0, nums, 0, &ans, returnSize, returnColumnSizes);
    if (*returnSize == 0)
    {
        return NULL;
    }
    return ans;
}

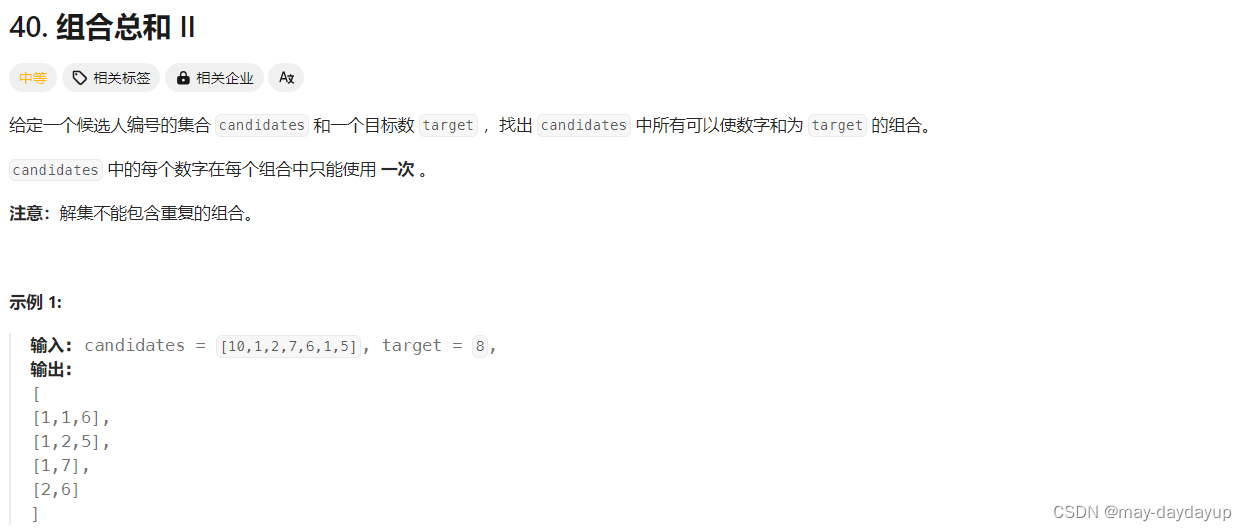
[40] 组合总和II

题目描述

40 组合总和II

解题思路

前提：组合的子集问题，同一元素只能使用一次，但是结果不包含重复组合
思路：回溯 + 剪枝
重点：结果子集中排除重复组合，需要树形结构中，同一树层的相同的元素值不可重复选取，使用used数组实现去重。

代码实现

C语言

利用used数组 false，同一树层去重

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */

int cmp(const void *p1, const void *p2)
{
    return *(int *)p1 > *(int *)p2;
}

void backtracing(int* candidates, int candidatesSize, int target, int index, int *nums, int numsSize, bool *used, int ***ans, int* returnSize, int** returnColumnSizes)
{
    // 退出条件
    if (0 == target)
    {
        *ans = (int **)realloc(*ans, sizeof(int *) * ((*returnSize) + 1));
        (*ans)[*returnSize] = (int *)malloc(sizeof(int) * (numsSize));
        for (int i = 0; i < numsSize; i++)
        {
            (*ans)[*returnSize][i] = nums[i];
        }
        *returnColumnSizes = (int *)realloc(*returnColumnSizes, sizeof(int) * ((*returnSize) + 1));
        (*returnColumnSizes)[*returnSize] = numsSize;
        (*returnSize)++;
        return ;
    }
    for (int j = index; (j < candidatesSize) && (target >= candidates[j]); j++)
    {
        // 去重
        if ((j > 0) && (candidates[j] == candidates[j - 1]) && (used[j - 1] == false))
        {
            continue;
        }
        // 递归
        nums[numsSize] = candidates[j];
        used[j] = true;
        numsSize++;
        backtracing(candidates, candidatesSize, target - candidates[j], j + 1, nums, numsSize, used, ans, returnSize, returnColumnSizes);
        // 回溯
        numsSize--;
        used[j] = false;
        nums[numsSize] = 0;
    }
    return ;
}

int** combinationSum2(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes) {
    // 判空
    if (candidatesSize == 0)
    {
        return NULL;
    }
    // 排序
    qsort(candidates, candidatesSize, sizeof(int), cmp);
    // 输出
    int **ans = NULL;
    int nums[100] = {0};
    bool used[100] = {false};
    int index = 0;
    *returnSize = 0;
    backtracing(candidates, candidatesSize, target, 0, nums, 0, used, &ans, returnSize, returnColumnSizes);
    if (*returnSize == 0)
    {
        return NULL;
    }
    return ans;
}

[131] 分割回文串

题目描述

131 分割回文串

解题思路

前提：分割问题
思路：分解成树状结构，判断子串是否为回文子串，若该子串不为回文，则该分割方式不符合要求。
重点：如何将分割问题，分解为树状结构，利用回溯求解。

代码实现

C语言

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */

char** path;
int pathTop;
char*** ans;
int ansTop = 0;
int* ansSize;

//将path中的字符串全部复制到ans中
void copy() {
    //创建一个临时tempPath保存path中的字符串
    char** tempPath = (char**)malloc(sizeof(char*) * pathTop);
    int i;
    for(i = 0; i < pathTop; i++) {
        tempPath[i] = path[i];
    }
    //保存tempPath
    ans[ansTop] = tempPath;
    //将当前path的长度（pathTop）保存在ansSize中
    ansSize[ansTop++] = pathTop;
}

//判断字符串是否为回文字符串
bool isPalindrome(char* str, int startIndex, int endIndex) {
    //双指针法：当endIndex（右指针）的值比startIndex（左指针）大时进行遍历
    while(endIndex >= startIndex) {
        //若左指针和右指针指向元素不一样，返回False
        if(str[endIndex--] != str[startIndex++])
            return false;
    }
    return true;
}

//切割从startIndex到endIndex子字符串
char* cutString(char* str, int startIndex, int endIndex) {
    //开辟字符串的空间
    char* tempString = (char*)malloc(sizeof(char) * (endIndex - startIndex + 2));
    int i;
    int index = 0;
    //复制子字符串
    for(i = startIndex; i <= endIndex; i++)
        tempString[index++] = str[i];
    //用'\0'作为字符串结尾
    tempString[index] = '\0';
    return tempString;
}

void backTracking(char* str, int strLen,  int startIndex) {
    if(startIndex >= strLen) {
        //将path拷贝到ans中
        copy();
        return ;
    }

    int i;
    for(i = startIndex; i < strLen; i++) {
        //若从subString到i的子串是回文字符串，将其放入path中
        if(isPalindrome(str, startIndex, i)) {
            path[pathTop++] = cutString(str, startIndex, i);
        }
        //若从startIndex到i的子串不为回文字符串，跳过这一层 
        else {
            continue;
        }
        //递归判断下一层
        backTracking(str, strLen, i + 1);
        //回溯，将path中最后一位元素弹出
        pathTop--;
    }
}

char*** partition(char* s, int* returnSize, int** returnColumnSizes){
    int strLen = strlen(s);
    //因为path中的字符串最多为strLen个（即单个字符的回文字符串），所以开辟strLen个char*空间
    path = (char**)malloc(sizeof(char*) * strLen);
    //存放path中的数组结果
    ans = (char***)malloc(sizeof(char**) * 40000);
    //存放ans数组中每一个char**数组的长度
    ansSize = (int*)malloc(sizeof(int) * 40000);
    ansTop = pathTop = 0;

    //回溯函数
    backTracking(s, strLen, 0);

    //将ansTop设置为ans数组的长度
    *returnSize = ansTop;
    //设置ans数组中每一个数组的长度
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    int i;
    for(i = 0; i < ansTop; ++i) {
        (*returnColumnSizes)[i] = ansSize[i];
    }
    return ans;
}