Acwing 786.第K个数

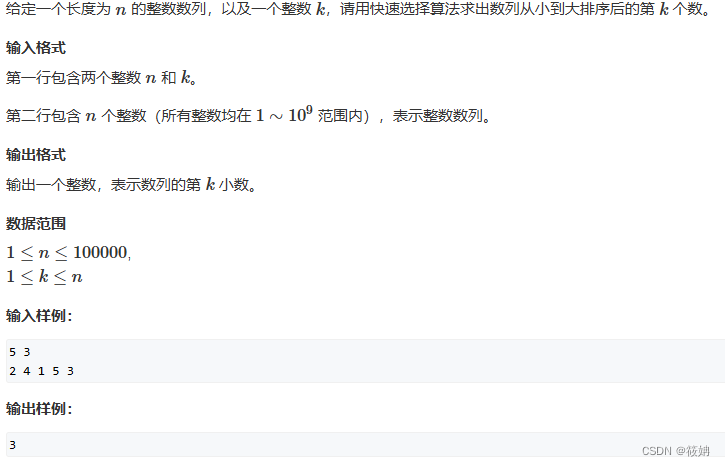
题目描述

786. 第k个数 - AcWing题库

运行代码

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int q[N];

int main()
{
    int n, k;
    scanf("%d%d", &n, &k);
    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);
    nth_element(q, q + k - 1, q + n);
    printf("%d ", q[k - 1]);
    return 0;
}

代码思路

1. 引入头文件和命名空间:#include <iostream> 用于输入输出操作。#include <algorithm> 引入算法库，包含nth_element函数。using namespace std; 允许直接使用标准库中的名称，而无需std::前缀。

2. 定义常量和变量:const int N = 100010; 定义数组的最大容量。int q[N]; 定义一个足够大的数组来存储输入的整数。

3. 主函数main:

   • 读取数据:首先，读取两个整数n和k，分别代表数组的元素个数和要找的第k小的元素的位置（从1开始计数）。然后，通过一个循环读取n个整数并存储到数组q中。

   • 使用nth_element:nth_element(q, q + k - 1, q + n); 这行代码是关键，它将数组q中的元素进行部分排序，使得第k小的元素（按照默认升序排序的标准）正好位于q[k - 1]的位置。nth_element不会保证整个数组有序，只是保证第k个元素就位，它前面的元素都不大于它，后面的元素都不小于它，这就足够找到第k小的元素。

   • 输出结果:printf("%d ", q[k - 1]); 输出找到的第k小的元素。

4. 返回0:return 0; 表示程序正常结束。

代码思路总结: 这段代码简洁高效地实现了寻找数组中第k小元素的任务，利用了nth_element函数的高效性，特别适合于当只需要找到一个特定位置的元素而不需要全数组排序的场景，大大提高了算法效率。

另外思路

#include<iostream>
using namespace std;
const int N=1e6+6;
int n;int k;
int q[N];
void qs(int q[], int l, int r){
    if (l>=r)return;
    int x = q[l];int i = l-1;int j = r+1;
    while(i<j){
        do i++;while(q[i]<x);
        do j--;while(q[j]>x);
        if(i < j)swap(q[i], q[j]);
    }
    qs(q,l,j);
    qs(q,j+1,r);
}
int main(){
    cin >> n >> k;
    for(int i = 0; i < n; ++i){
        cin >> q[i];
    }
    qs(q,0,n-1);
    cout << q[k-1];
    return 0;
}

代码思路

1. 头文件和命名空间:

   • #include<iostream> 用于输入输出操作。
   • using namespace std; 允许直接使用标准库中的名称，如cout和cin，而不必加std::前缀。

2. 常量定义和变量声明:

   • const int N = 1e6 + 6; 定义了一个常量N，用于设定数组的最大容量。
   • int n; int k; 声明了两个整型变量，分别用于存储数组长度和要找的第k小的元素的位置。
   • int q[N]; 定义了一个足够大的数组来存储输入的整数序列。

3. 快速排序函数qs:

   • 函数接受一个整数数组q[]及其左右边界索引l和r作为参数。
   • 选择数组的第一个元素q[l]作为基准值x。
   • 初始化两个指针i和j，分别位于l-1和r+1，用于从两边向中间扫描。
   • 使用循环，在q[i]不大于x且q[j]不小于x时，向中间移动这两个指针，并在适当时候交换两者所指的元素，以确保左侧元素都不大于x，右侧元素都不小于x。
   • 当i和j交错时，基准值x的最终位置确定在j，此时基准值左侧的元素都小于等于它，右侧的元素都大于等于它。
   • 递归调用qs函数分别对基准值左侧和右侧的子序列进行快速排序。

4. 主函数main:

   • 读取整数n（数组长度）和k（要找的第k小元素的位置）。
   • 通过循环读取数组q[]中的每个整数。
   • 调用快速排序函数qs(q, 0, n - 1)对数组进行排序。
   • 输出排序后数组中第k小的元素，即q[k-1]，因为数组索引是从0开始的。

代码在处理大量数据或极端情况时可能不是最优选择，特别是在快速排序最坏情况下的时间复杂度为O(n^2)，虽然平均时间复杂度为O(n log n)。对于寻找第k小的元素，有时候使用快速选择算法（基于快速排序思想的优化版本，避免完全排序）会更高效。

改进思路

将原有的快速排序改为快速选择算法，因为我们的目标不是完全排序数组，而是找到第k小的元素。这样可以减少不必要的比较和交换，提高效率，尤其是在k相对较小的情况下。快速选择算法的关键在于只对与k相关的部分进行排序，具体改进如下：

1. 修改分区函数：调整分区逻辑，仅保证基准元素到达其最终排序位置，而不需要对整个数组进行排序。
2. 直接返回第k小的元素：在快速选择过程中，一旦找到正确的分区，直接返回第k小的元素，无需完成整个数组的排序。

改进代码

#include<iostream>
#include<climits>
using namespace std;

const int N = 1e6 + 6;

int partition(int arr[], int l, int r) {
    int pivot = arr[r]; // 选择最右侧元素作为基准
    int i = l - 1;
    for(int j = l; j < r; ++j) {
        if(arr[j] <= pivot) {
            i++;
            swap(arr[i], arr[j]);
        }
    }
    swap(arr[i + 1], arr[r]); // 把基准元素放到正确的位置
    return i + 1;
}

int select(int arr[], int l, int r, int k) {
    if(l == r) return arr[l];
    int pivot_index = partition(arr, l, r);
    if(k == pivot_index) {
        return arr[k];
    } else if(k < pivot_index) {
        return select(arr, l, pivot_index - 1, k);
    } else {
        return select(arr, pivot_index + 1, r, k);
    }
}

int main() {
    int n, k;
    cin >> n >> k;
    int q[N];
    for(int i = 0; i < n; ++i) {
        cin >> q[i];
    }
    --k; // 数组索引从0开始
    cout << select(q, 0, n - 1, k) << endl;
    return 0;
}