小编阅读了一篇发表于2002年关于P值的一项问卷调查研究 [1],作者在6所德国大学中邀请了3组不同的受试者,分别为: 心理学专业的学生(n = 44);主要从事科学研究但不进行统计相关教学的教授和讲师(n = 39);进行统计相关教学的教授和讲师(n = 30)。
作者邀请上述三组受试者参加问卷调查,具体内容如下:
假设现在有一种治疗方法,你推测该方法或许可以改善人们在某种测验上的表现能力。于是你设计了一个研究,比较了对照组和实验组(假设每组20个样本)的均数。之后使用了独立样本t检验,获得了以下结果:t = 2.7, d.f. = 18, p = 0.01。请你回答以下六个判断题,分别在对应题目下方的“对”或“错”上打勾。“错”则表示该题内容与前面研究结果的逻辑不相符。需注意,可能有多个或零个问题是正确的。
1)你完全否定了零假设(零假设指的是两个总体的均数没有差异。)
对 / 错
2)你找到了零假设为真的概率。
对 / 错
3)你完全证明了实验假说(实验假说指的是两个总体的均数存在差异。)
对 / 错
4)你可以推断出实验假说为真的概率。
对 / 错
5)假如你决定要拒绝零假设,你已经知道这个决定若为错的概率。
对 / 错
6)你得到了一个可靠的研究结果,原因为:假如这个实验被重复了非常多次,你将有99%的可能获得一个显著的结果。
对 / 错
先呈现3组受试者的结果,正确答案在最后公布,如下:
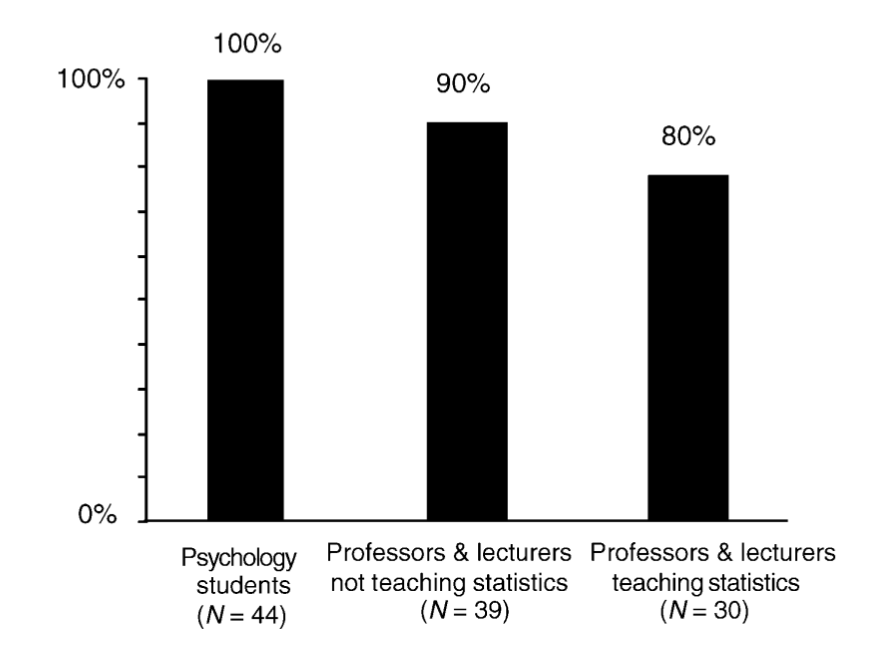
来源: 文献[2]的Figure 1
上述的纵坐标为至少错一题所占的人数比例,横坐标为三组受试者。其中,80%从事统计教学的教授或者讲师至少答错了一题。
如果我们也答错,那也没什么大不了的图片!
再来看看到底哪几个问题容易答错,如下表:
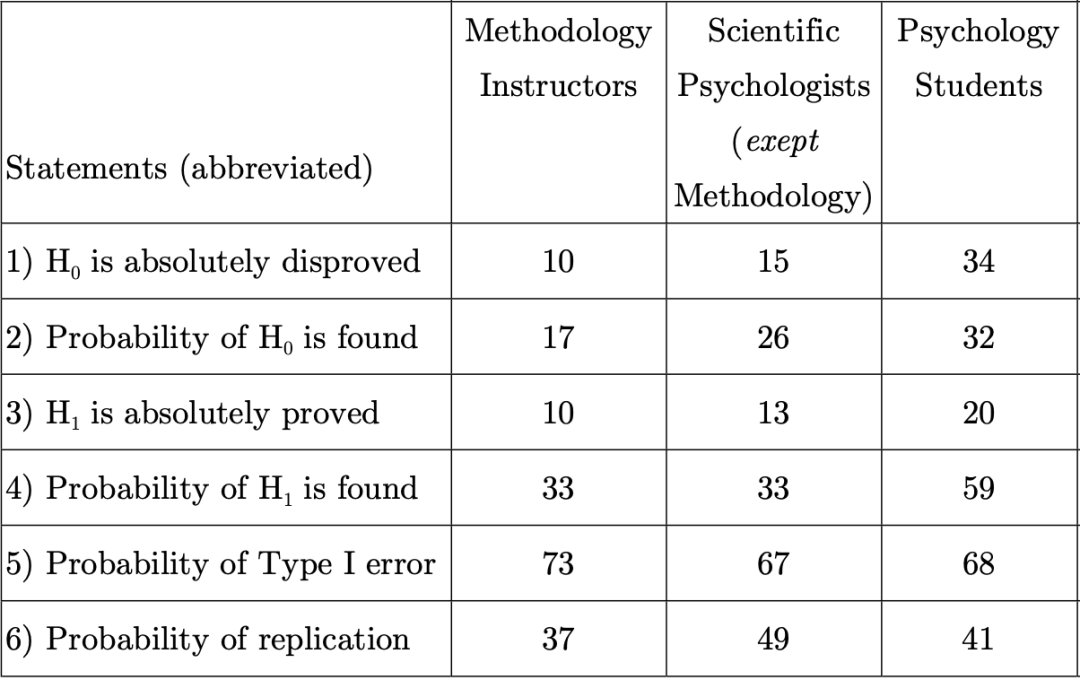
来源: 文献[1]的Table 1
其中,表格上方为三组参与者,内部的数值为错误答案所占的比例,而表格左侧简单归纳了上述6点说法。
最后,公布正确答案:所有说法都是“错的”!
我们回想P值的定义:当零假设为真时,与样本观察结果相同(或更极端结果)的概率,也可以用符号进行表示:p(D|H0)。
上述6种说法是对P值的过度解读以及概念的混淆!
好啦,今天的内容就到这里。
如果有帮助,记得分享给需要的人图片!
参考文献
[1]. Haller, H., Krauss, S., 2002. Misinterpretations of significance: a problem students share with their teachers? Methods of Psychological Reseach.
[2]. Gerd Gigerenzer, Mindless statistics, The Journal of Socio-Economics 33 (2004) 587–606