【备战蓝桥杯】蓝桥杯省一笔记：算法模板笔记（Java）

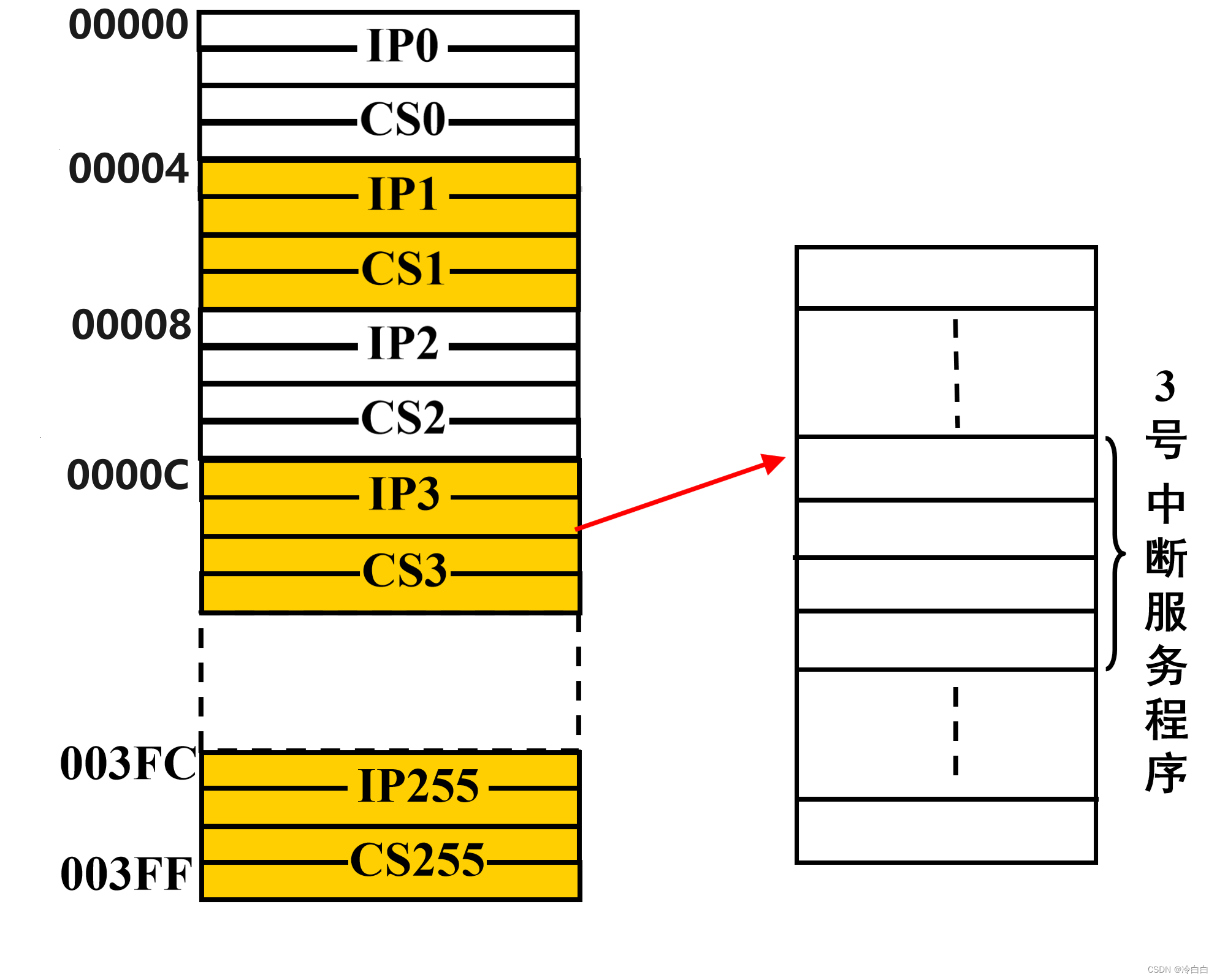
蓝桥杯

- - 0、快读快写模板
  - 1、回文判定
  - 2、前缀和
  - 3、差分
  - 4、二分查找
  - 5、快速幂
  - 6、判断素数
  - 7、gcd&lcm
  - 8、进制转换
  - 9、位运算
  - 10、字符串常用API
  - 11、n的所有质因子
  - 12、n的质因子个数
  - 13、n的约数个数
  - 14、n阶乘的约数个数
  - 15、n的约数和
  - 16、阶乘 & 双阶乘
  - 17、自定义升序降序
  - 18、动态规划_01背包
  - 19、动态规划_多重背包
  - 20、动态规划_完全背包
  - 21、子串分值和
  - 22、埃氏筛法
  - 23、欧拉筛法
  - 24、欧拉函数
  - 25、欧拉求和
  - 26、区间素数筛
  - 27、桶排序
  - 28、费马小定理求逆元
  - 29、阶乘的约数和
  - 30、最小质因子之和（埃氏筛法）
  - 31、排列组合
  - 32、计算几何公式
  - 33、Floyd 多源最短路
  - 34、Dijkstra 单源最短路可处理非负边权
  - 35、Kruskal 算法
  - 36、KMP 算法
  - 37、Prim 算法
  - 38、BellmanFord 算法
  - 39、LIS 最长公共子序列
  - 40、LCS最长上升子序列_朴素
  - 41、LCS最长上升子序列_二分
  - 42、Manacher 算法
  - 43、ST表_求区间最小值
  - 44、ST表_求区间最大值
  - 45、并查集

前言
第二次参加蓝桥杯，从C++组转Java组，分享一下平时备赛整理的模板笔记，如有错误，欢迎评论或者私聊
在这里插入图片描述

0、快读快写模板

import java.io.*;

public class Main {
    static PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
    static StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
    public static void main(String[] args) throws IOException{
        pw.flush();
    }

    public static String Line() throws IOException {
        String s = bf.readLine();
        return s;
    }
    public static int Int() throws IOException{
        st.nextToken();
        return (int)st.nval;
    }
    public static long Long() throws IOException{
        st.nextToken();
        return (long) st.nval;
    }
    public static double Double() throws IOException{
        st.nextToken();
        return st.nval;
    }
}

数据输入达 1e5 需要用快读快写才能拿更多的分

1、回文判定

回文数、回文字符串皆可用双指针进行判断

public static void main(String[] args) throws IOException{
    int n = Int();
    pw.println(hw(n));
    pw.flush();
}

private static boolean hw(int n1) {
    String s = n1+"";
    int n = s.length()-1;
    for (int l = 0,r = n; l<r; l++,r--) {
        if (s.charAt(l)!=s.charAt(r))
            return false;
    }
    return true;
}

2、前缀和

前缀和 sum[i] = sum[i-1] + a[i]
区间前缀和 sum[r]-sum[l-1]
作用：计算各个区间的和

public static void main(String[] args) throws IOException{
    int n = Int();
    int m = Int();
    int[] a = new int[n+1];
    int[] sum = new int[n+1];
    for (int i = 1; i <= n; i++) {
        a[i]=Int();
        sum[i]=sum[i-1]+a[i];
    }
    while (m-->0){
        int l = Int();
        int r = Int();
        pw.println(sum[r]-sum[l-1]);
    }
    pw.flush();
}

3、差分

差分与前缀和互逆
下标从0开始存储（输入左右边界需要减一）
下标从1开始存储（输入左右边界不用减一）
差分 b[i]=a[i]-a[i-1]
区间加法 b[l]+=c b[r+1]-=c
区间减法 b[l]-=c b[r+1]+=c
b[i]+=b[i-1] 还原差分数组
作用：计算差分数组与原数组相加后的元素值

public static void main(String[] args) throws IOException{
    int n = Int();
    int[] a = new int[n+1];
    int m = Int();
    for (int i = 1; i <= n; i++) {  //数组从1开始存储
        a[i]=Int();
    }
    while (m-->0){
        int l = Int();  //左右边界输入不用减一
        int r = Int();
        int c = Int();
        b[l]+=c;
        b[r+1]-=c;
    }
    for (int i = 1; i <= n; i++) {  //前缀和还原差分数组
        b[i]+=b[i-1];
    }
    for (int i = 1; i <= n; i++) {
        long ans = a[i]+b[i];    //原数组与差分数组相加
        if (ans<0){
            pw.print(0+" ");
        }else {
            pw.print(ans+" ");
        }
    }
    pw.flush();
}

4、二分查找

二分查找的序列必须是有序的
下面有两种求法，适应不同的情况
① 在单调递增序列a中查找>=x的数中最小的一个（即x或x的后继）
② 在单调递增序列a中查找<=x的数中最大的一个（即x或x的前驱）

public static void main(String[] args) throws IOException{
    int x = Int();
    int[] a = {1,2,3,4,5,6,7,8};
    int l = 0;
    int r = a.length-1;
    // 在单调递增序列a中查找>=x的数中最小的一个（即x或x的后继）
    while (l<r){
        int mid = (l+r)/2;
        if (a[mid]>=x){
            r = mid;
        }else {
            l = mid + 1;
        }
    }
    System.out.println(r);
    // 在单调递增序列a中查找<=x的数中最大的一个（即x或x的前驱）
    while (l<r){
        int mid = (l+r+1)/2;
        if (a[mid]<=x){
            l = mid;
        }else {
            r = mid - 1;
        }
    }
    System.out.println(l);
    pw.flush();
}

5、快速幂

求（a 的 b次方）mod p

public static void main(String[] args) throws IOException{
    long a = Long();
    long b = Long();
    long p = Long();
    pw.println(qmi(a,b,p));
    pw.flush();
}

private static long qmi(long a, long b, long p) {
    long res = 1;
    while (b>0){
        if ((b&1)==1){
            res=res*a%p;
        }
        a=a*a%p;
        b>>=1;
    }
    return res;
}

6、判断素数

如果 n 小于2，不是素数。枚举2 - n/i , 如果 n%i==0 说明 n 不是素数。

public static void main(String[] args) throws IOException{
    int n = Int();
    pw.println(isprime(n));
    pw.flush();
}

private static boolean isprime(int n) {
    if (n<2) return false;
    for (int i = 2; i <= n/i; i++) {
        if (n%i==0){
            return false;
        }
    }
    return true;
}

7、gcd&lcm

最大公约数gcd、最小公倍数lcm

private static int lcm(int a, int b) {
    return a/gcd(a,b)*b;
}

private static int gcd(int a, int b) {
    return b==0? a:gcd(b,a%b);
}

8、进制转换

在这里插入图片描述

9、位运算

在这里插入图片描述

10、字符串常用API

11、n的所有质因子

求解n的质因子，枚举2 到 n/i，if ( n%i )==0, i 是质因子；
while ( n%i==0 ){
n/=i;

}，则是去除质因子。枚举结束，如果 n>1，n也是质因子。

public static void main(String[] args) throws IOException{
    long n = Long();
    deal(n);
    pw.flush();
}

private static void deal(long n) {
    for (int i = 2; i <= n/i; i++) {
        if (n%i==0){
            System.out.print(i+" ");
        }
        while (n%i==0){
            n/=i;
        }
    }
    if (n>1) System.out.print(n);
}

12、n的质因子个数

求解n的质因子，枚举2 - n/i，if ( n%i )==0, 质因子个数++；
while ( n%i==0 ){
n/=i;
}，则是去除质因子。枚举结束，如果 n>1，质因子个数++。

public static void main(String[] args) throws IOException{
    long n = Long();
    deal(n);
    pw.flush();
}

private static void deal(long n) {
    int sum = 0;
    for (int i = 2; i <= n/i; i++) {
        if (n%i==0){
            sum++;
        }
        while (n%i==0){
            n/=i;
        }
    }
    if (n>1) sum++;
    System.out.println(sum);
}

13、n的约数个数

求约数个数：即求（素因子1的指数+1）（素因子2的指数+1）*…（素因子n的指数+1）

public static void main(String[] args) throws IOException{
    int n = Int();
    int bak = n;
    int[] f = new int[n+1];
    for (int i = 2; i <= bak/i; i++) {
        if (bak%i==0){
            while (bak%i==0){
                f[i]++;
                bak/=i;
            }
        }
    }
    if (bak>1) f[bak]++;
    long ans = 1;
    for (int x : f){
        if (x > 0){
            ans=ans*(x+1);
        }
    }
    pw.println(ans);
    pw.flush();
}

14、n阶乘的约数个数

求约数个数：即求（素因子1的指数+1）（素因子2的指数+1）…（素因子n的指数+1）
求n阶乘的约数个数，即两次for循环即可解决。

public static void main(String[] args) throws IOException{
    int n = Int();
    int bak = 0;
    int[] f = new int[n+1];
    for (int i = 2; i <= n; i++) {
        bak = i;
        for (int j = 2; j <= bak/j; j++) {
            if (bak%j==0){
                while (bak%j==0){
                    f[j]++;
                    bak/=j;
                }
            }
        }
        if (bak>1) f[bak]++;
    }
    long ans = 1;
        for (int x : f){
            if (x > 0){
                ans = ans*(x+1);
            }
        }
    pw.println(ans);
    pw.flush();
}

15、n的约数和

约数与因数是相同的概念，求n的约数，即求 1-n 能被 n 整除的数。

public static void main(String[] args) throws IOException{
    int n = Int();
    pw.println(deal(n));
    pw.flush();
}

private static int deal(int n) {
    int sum = 0;
    for (int i = 1; i <= n; i++) {
        if (n%i==0){
            sum+=i;
        }
    }
    return sum;
}

16、阶乘 & 双阶乘

求阶乘
如果 n 小于等于0，返回1，否则返回 n*jc ( n-1 )

public static void main(String[] args) throws IOException{
    int n = Int();
    System.out.println(jc(n));
    pw.flush();
}

private static long jc(int n) {
    if (n<=0) return 1;
    return n*jc(n-1);
}

求双阶乘
如果 n 小于等于0，返回1，否则返回 n*jc ( n-2 )

public static void main(String[] args) throws IOException{
    int n = Int();
    System.out.println(jc(n));
    pw.flush();
}

private static long jc(int n) {
    if (n<=0) return 1;
    return n*jc(n-2);
}

17、自定义升序降序

注意：自定义排序需要使用引用数据类型

public static void main(String[] args) throws IOException{
    int n = Int();
    Integer[] arr = new Integer[n];
    for (int i = 0; i < n; i++) {
        arr[i]=Int();
    }
    Arrays.sort(arr,(o1, o2) -> o2-o1);
    for (int x : arr){
        System.out.print(x+" ");
    }
    pw.flush();
}

18、动态规划_01背包

小明有一个容量为 V 的背包。

这天他去商场购物，商场一共有 N 件物品，第 i 件物品的体积为 wi，价值为 vi。

小明想知道在购买的物品总体积不超过 V 的情况下所能获得的最大价值为多少，请你帮他算算。

public static void main(String[] args) throws IOException {
    int n = Int();
    int m = Int();
    int[] W = new int[n + 1];
    int[] V = new int[n + 1];
    for (int i = 0; i < n; i++) {
        W[i] = Int();
        V[i] = Int();
    }
    int[][] dp = new int[n + 1][m + 1];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (j >= W[i - 1]) {  //选第i件物品
                dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - W[i - 1]] + V[i - 1]);
            }
            dp[i][j] = Math.max(dp[i][j], dp[i - 1][j]);  //不选第i件物品

        }
    }
    pw.println(dp[n][m]);
    pw.flush();
}

19、动态规划_多重背包

第 i 种物品的体积为 wi，价值为 vi，数量为 si。

public static void main(String[] args) throws IOException {
    int n = Int();
    int m = Int();
    int[] W = new int[n + 50];
    int[] V = new int[n + 50];
    int[] S = new int[n + 50];
    int[] dp = new int[n + 50];
    for (int i = 0; i < n; i++) {
        W[i] = Int();
        V[i] = Int();
        S[i] = Int();
    }
    Arrays.fill(dp,0);
    for (int i = 0; i < n; i++) {  //遍历每一个物品
        for (int j = m; j >= W[i]; j--) {
            for (int k = 1; k <= S[i] && j>=k*W[i]; k++) {
                dp[j]=Math.max(dp[j],dp[j-k*W[i]]+V[i]*k);
            }
        }
    }
    pw.println(dp[m]);
    pw.println();
    pw.flush();
}

20、动态规划_完全背包

每种物品都有无限多个

public static void main(String[] args) throws IOException {
    int n = Int();
    int m = Int();
    int[] w = new int[n];
    int[] v = new int[n];
    for (int i = 0; i < n; i++) {
        w[i]=Int();
        v[i]=Int();
    }
    int[] dp = new int[m+1];
    for (int i = 0; i < n; i++) {
        for (int j = w[i]; j <= m; j++) {
            dp[j]=Math.max(dp[j],dp[j-w[i]]+v[i]);
        }
    }
    pw.println(dp[m]);
    pw.flush();
}

21、子串分值和

统计所有子串不重复的字符个数

public static void main(String[] args) throws IOException{
    char[] c = Line().toCharArray();
    int n = c.length;
    long res = 0l;
    for (int i = 0; i < n; i++) {
        int pre = i-1;
        while (pre>=0&&c[pre]!=c[i]) --pre;
        res+=1l*(i-pre)*(n-i);
    }
    pw.println(res);
    pw.flush();
}

22、埃氏筛法

筛出 1 到 n 的所有素数
埃氏筛法：如果一个数不是素数，它一定是n个素数的乘积，素数的倍数一定是合数。

public static void main(String[] args) throws IOException{
    int n = Int();
    isprime(n);
    pw.flush();
}

private static void isprime(int n) {
    boolean[] isprime = new boolean[n+1];
    for (int i = 2; i <= n/i; i++) {
        if (!isprime[i]){
            for (int j = 2; j <= n/i; j++) {
                isprime[i*j]=true;
            }
        }
    }
    for (int i = 2; i <= n; i++) {
        if (!isprime[i]){
            System.out.print(i+" ");
        }
    }
}

23、欧拉筛法

筛出 1 到 n 的所有素数
欧拉筛法：每个合数只被它最小的质因子筛一次
将目前找到的每一个素数的i倍标记为合数，如果i本身就是素数的倍数，就去执行下一个 i

public static void main(String[] args) throws IOException{
    int n = Int();
    deal(n);
    pw.flush();
}

private static void deal(int n) {
    boolean[] isprime = new boolean[n+1];
    int[] prime = new int[n];
    int count = 0;
    for (int i = 2; i <= n; i++) {
        if (!isprime[i]){
            prime[count++]=i;
        }
        for (int j = 0; j < count && i*prime[j]<=n; j++) {
            isprime[i*prime[j]]=true;
            if (i%prime[j]==0) break; //欧拉筛精髓  如果i本身就是素数的倍数 跳过去
        }
    }
    for (int i = 0; i < count; i++) {
            System.out.print(prime[i]+" ");
    }
}

24、欧拉函数

计算一个数的欧拉函数值，先找出其质因子。

public static void main(String[] args) throws IOException{
    long n = Long();
    pw.println(phi(n));
    pw.flush();
}

private static long phi(long n) {
    long res = n;
    for (int i = 2; i <= n/i; i++) {
        if (n%i==0){
            while (n%i==0){
                n/=i;
            }
           res=res/i*(i-1);
        }
    }
    if (n>1){
        res=res/n*(n-1);
    }
    return res;
}

25、欧拉求和

计算一个区间[ L , R ]的欧拉函数值之和

public static void main(String[] args) throws IOException{
    int l = Int(),r = Int();
    int[] phi = EulerSieve(r);
    long ans = 0;
    for (int i = l; i <= r; i++) {
        ans+=phi[i];
    }
    pw.println(ans);
    pw.flush();
}

private static int[] EulerSieve(int n) {
    boolean[] isprime = new boolean[n+1];
    int[] prime = new int[n+1];
    int count = 0;
    int[] phi = new int[n+1];
    phi[1]=1;
    for (int i = 2; i <= n; i++) {
        if (!isprime[i]){
            prime[count++]=i;
            phi[i]=i-1;
        }
        for (int j = 0; j < count && i*prime[j]<=n; j++) {
            int m = i*prime[j];
            isprime[m]=true;
            if (i%prime[j]==0){
                phi[m]=prime[j]*phi[i];
                break;
            }else {
                phi[m]=(prime[j]-1)*phi[i];
            }
        }
    }
    return phi;
}

26、区间素数筛

求大范围的区间素数或者区间素数个数

public class 区间素数筛 {
    static int a,b;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        a = sc.nextInt();
        b = sc.nextInt();
        isprime(b);

    }

    private static void isprime(int n) {
        boolean[] isprime = new boolean[n+1];
        int[] prime = new int[n+1];
        int count = 0;
        for (int i = 2; i <= n; i++) {
            if (!isprime[i]){
                prime[count++]=i;
            }
            for (int j = 0; j < count && i*prime[j]<=n; j++) {
                int m = i*prime[j];
                isprime[m]=true;
                if (i%prime[j]==0){
                    break;
                }
            }
        }
        for (int i = a; i <= b; i++) {
            if (!isprime[i]){
                System.out.print(i+" ");
            }
        }
    }
}

27、桶排序

输入数据 n 过大，用快速排序会超时，这时可用桶排序

private static final int MaxN = (int) 6e5+5;
private static List<Integer>[] bucket = new ArrayList[MaxN];
public static void main(String[] args) throws IOException{
    int n = Int();
    for (int i = 0; i < MaxN; i++) {
        bucket[i]=new ArrayList<>(); //初始化桶集合 集合里全是桶列表
    }
    for (int i = 1; i <= n; i++) {  //输入n个数
        int x = Int();
        bucket[x/1000].add(x); //设每个桶的值域是1000，分别将x放到相应的桶
    }
    for (int i = 0; i < MaxN; i++) {
        Collections.sort(bucket[i]);  //分别对每个桶的元素进行排序
    }
    for (int i = 0; i < MaxN; i++) {  //遍历每个桶排序后的元素
        for (int item:bucket[i]){
            System.out.print(item+" ");
        }
    }
    pw.flush();
}

28、费马小定理求逆元

计算 a mod p下的逆元
注意：a mod p ==0, 逆元不存在
a^p-1=1(mod p), a^p-2 = a^-1(mod p)
a^-1即为逆元

public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);
    long a = sc.nextInt();
    long p = sc.nextInt();
    if (a%p==0){
        System.out.println("a模p的逆元不存在");
    }else {
        System.out.println(qmi(a,p-2,p));
    }
}

private static long qmi(long a, long b, long p) {
    long res = 1;
    while (b>0){
        if ((b&1)==1){
            res=res*a%p;
        }
        a=a*a%p;
        b>>=1;
    }
    return res;
}

29、阶乘的约数和

阶乘的约数和：p 为素数，cnt 为素数出现的次数
公式：ans=ans*{{[(p^cnt+1) - 1] * [(p-1)^mod-2]%mod+mod}}

public static void main(String[] args) throws IOException{
    int n = Int();
    int[] prime = isprime(n);
    long ans = 1;
    int mod = 998244353;
    for (int p:prime){
        long cnt = 0;
        if (p>0){
            int x = n;
            while (x>0){
                cnt+=x/p;
                x/=p;
            }
            ans=(ans*((qmi(p,cnt+1,mod)-1)*qmi(p-1,mod-2,mod)%mod+mod))%mod;  //中间这一块防止变为负数需加mod
        }
    }
    pw.println(ans);
    pw.flush();
}
private static long qmi(long a, long b, long p) {
    long res=1;
    while (b>0){
        if ((b&1)==1){
            res=res*a%p;
        }
        a=a*a%p;
        b>>=1;
    }
    return res;
}
public static int[] isprime(int n){
    boolean[] isprime = new boolean[n+1];
    int[] prime = new int[n+1];
    int count = 0;
    for (int i = 2; i <= n; i++) {
        if (!isprime[i]){
            prime[count++]=i;
        }
        for (int j = 0; j < count && i*prime[j]<=n; j++) {
            int m = i*prime[j];
            isprime[m]=true;
            if (i%prime[j]==0){
                break;
            }
        }
    }
    return prime;
}

30、最小质因子之和（埃氏筛法）

static boolean[] isprime = new boolean[(int) (3e6+1)];
static long[] ans = new long[(int) (3e6+1)];
public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);
    int t = Integer.parseInt(sc.nextLine());
    get(3000000);
    for (int i = 2; i <= 3000000; i++) {
        ans[i] += ans[i-1];
    }
    while (t-->0){
        System.out.println(ans[Integer.parseInt(sc.nextLine())]);
    }
}

private static void get(int n) {
    for (int i = 2; i <= n; i++) {
        if (!isprime[i]){
            ans[i]=i;
        }
        for (int j = 2; j <= n/i; j++) {
            if (!isprime[i*j]){
                isprime[i*j]=true;
                ans[i*j]=i;
            }
        }
    }
}

31、排列组合

求组合数

private static long c(long n, long m) {
    long res = 1;
    for (long i = n; i >= n-m+1; i--) {
        res=res*i%mod;
    }
    for (int i = 1; i <= m; i++) {
        res=res*qmi(i,mod-2)%mod;
    }
    return res;
}

public static long qmi(long a,long b){
    long res = 1;
    while (b>0){
        if ((b&1)==1){
            res=res*a%mod;
        }
        a=a*a%mod;
        b>>=1;
    }
    return res;
}

求排列数

public static long qmi(long a,long b){
    long res = 1;
    while (b>0){
        if ((b&1)==1){
            res = res*a%mod;
        }
        a = a*a%mod;
        b>>=1;
    }
    return res;
}

public static long A(long n, long m) {
        if (m > n) return 0; // 如果m大于n，排列数不存在，返回0
        long res = 1;
        // 计算 n!
        for (long i = n; i > n - m; i--) {
            res = res * i % mod;
        }
        return res;
    }

32、计算几何公式

类型统一用double 可通过全部用例

1、已知三角形的三个顶点，求三角形面积公式

/**
S = 1/2[(x1y2+x2y3+x3y1)-(x1y3+x2y1+x3y2)]
先求绝对值 [ ]
再整体除以2
*/

2、给出三个点ABC，求C是否在直线AB上

/**
即求斜率AC==AB 如果相等说明点C在直线AB上
求两点斜率 AB y2-y1/x2-x1
*/

3、给出三个点ABC，求点和直线的关系
/**
求某一点在直线左边、右边、还是在直线上
用向量的叉乘计算
计算向量 AB 和 BC 的叉乘
叉乘为：(x2-x1)(y3-y1)-(y2-y1)(x3-x1)
叉乘大于0 点在直线左边
叉乘等于0 点在直线上
叉乘小于0 点在直线右边
@param args
*/

4、判断直线相交和点位置
/**
判断两条直线是否相交斜率不等
判断两条直线是否平行斜率相等

y=Ax+B 斜截式
求两条直线相交的点
x坐标 == B2-B1/A1-A2
y坐标 == Ax+B

判断一个点是否在一个线段上
如果 k1 == k2 说明在线段上否则不在

5、给出ABC三个点，求点C与线段AB的关系
在这里插入图片描述

33、Floyd 多源最短路

Floydl算法是一种用于在加权图中找到所有顶点对之间的最短路径的算法。它与Dijkstra算法不同，Dijkstra算法只能找到从单个源点到其他所有顶点的最短路径，而Floyd算法可以找到图中每一对顶点之间的最短路径。
Floyd算法的基本思想是使用动态规划。它通过逐步考虑图中的所有顶点，作为路径中的中继点，来更新任意两点之间的最短路径。算法使用一个二维数组来存储任意两点之间的最短路径长度，并在迭代过程中更新这个数组。
算法步骤如下：

初始化：创建一个二维数组dist，其中dist[i][j]表示顶点i到顶点j的路径长度。初始时，如果i和j直接相邻，则dist[i][j]为它们之间边的权重；如果i和j不直接相邻，则dist[i][j]为无穷大；对角线上的元素dist[i][i]初始化为0。
更新路径长度：对于图中的每个顶点k，遍历所有顶点对(i, j)，如果dist[i][k] + dist[k][j] < dist[i][j]，则更新dist[i][j]为dist[i][k] + dist[k][j]。这个步骤会重复进行，直到所有的顶点都作为中继点被考虑过。
结束：当所有顶点都作为中继点被考虑过后，算法结束。此时，dist数组中的dist[i][j]就存储了顶点i到顶点j的最短路径长度。
时间复杂度：O(V^3)，其中V是顶点的数量。它不适合处理顶点数量非常大的图。

    static int floyd(int[][] g) {
        for(int k=1;k<=n;k++) 
            for(int i=1;i<=n;i++) 
                for(int j=1;j<=n;j++) 
                    g[i][j] = Math.min(g[i][j], g[i][k]+g[k][j]);
        return g[1][n];
    }

    //初始化
    for(int i=0;i<n;i++) {
        Arrays.fill(g[i], INF);
        tie[i][i] = gon[i][i] = 0;  //自己到自己的距离为0      
    }

	//最短距离 表示从顶点1到顶点n的最短路径
	g[1][n];

34、Dijkstra 单源最短路可处理非负边权

Dijkstra算法是一种用于在加权图中找到单源最短路径的算法。所谓单源最短路径问题，就是给定一个图，其中的每条边都有一个非负权重，以及一个起始顶点，需要找到从该起始顶点到图中所有其他顶点的最短路径。
Dijkstra算法的基本思想是，从一个顶点开始，逐步探索图中的其他顶点，同时记录从起始顶点到每个顶点的最短路径长度。算法使用一个优先队列（通常是一个最小堆）来选择下一个访问的顶点，这个顶点是当前已知路径长度中最短的。
算法步骤如下：

初始化：将起始顶点的路径长度设置为0，其他顶点的路径长度设置为无穷大。创建一个优先队列，将起始顶点加入队列。
循环：当优先队列非空时，执行以下步骤：

从优先队列中取出具有最小路径长度的顶点。
对于这个顶点的每个邻接顶点，计算通过当前顶点到达邻接顶点的路径长度。如果这个路径长度比已知的最短路径长度更短，就更新最短路径长度，并将邻接顶点加入优先队列。

结束：当优先队列为空时，算法结束。此时，算法已经找到了从起始顶点到所有其他顶点的最短路径。
时间复杂度：取决于所使用的优先队列的实现。如果使用数组实现的优先队列，时间复杂度为O(V^2)，其中V是顶点的数量。如果使用二叉堆实现的优先队列，时间复杂度为O((V + E) log V)，其中E是边的数量。使用斐波那契堆可以实现更优的时间复杂度，为O(E + V log V)。

	static int[] h = new int[N],e = new int[M],ne = new int[M],w = new int[M];
	static int idx;
	static int[] dist = new int[N],st = new int[N];
	static void add(int a,int b,int c) {
		e[idx] = b;
		w[idx] = c;
		ne[idx] = h[a];
		h[a] = idx++;
	}
	static int dijkstra() {
		Arrays.fill(dist, INF);
		PriorityQueue<PII> q = new PriorityQueue<PII>((a,b)->(a.dist-b.dist));//小根堆
		q.add(new PII(0,1));
		dist[1]=0;

		while(q.size()>0) {
			PII top = q.poll();
			//如果这个点的最短路确定了，那么直接跳过
			if(st[top.ver]==1) continue;
			st[top.ver]=1;
			
			for(int i=h[top.ver];i!=-1;i=ne[i]) {
				int j = e[i];
				if(dist[j]>dist[top.ver]+w[i]) {
					dist[j] = dist[top.ver]+w[i];
					q.add(new PII(dist[j],j));
				}
			}
		}
		return dist[n];
	}
}
class PII{
	int dist,ver;
	
	public PII(int dist,int ver) {
		this.dist = dist;
		this.ver = ver;
	}
}

35、Kruskal 算法

适用于稀疏图，时间复杂度 O(m*logm)
Kruskal算法是一种用于在加权图中找到最小生成树的算法。它按照边的权重顺序（从小到大）选择边，并检查是否形成环。如果不形成环，就将其加入到最小生成树中。这个过程一直持续到所有的顶点都被包含在最小生成树中。

import java.io.*;
import java.math.BigInteger;
import java.util.*;


public class Main {
    public static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    public static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    public static StreamTokenizer cin = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    public static PrintWriter cout = new PrintWriter(new OutputStreamWriter(System.out));
    public static Scanner sc = new Scanner(System.in);

    public static int maxd = 200000+7;
    public static int INF = 0x3f3f3f3f;
    public static int mod = (int) 1e9+7;
    public static int[] par = new int[maxd]; //存储父节点
    public static int n;

    public static class Edge implements Comparable<Edge> {
        private int u; //起点
        private int v; //终点
        private int w; //边的权重
        public Edge(int u, int v, int w) {
            this.u = u;
            this.v = v;
            this.w = w;
        }
        public int compareTo(Edge obj) {
            return this.w - obj.w;
        }
    }
    public static Edge[] edges = new Edge[maxd<<1]; //无向图，开两倍

    public static void init(int n,int m){
        for(int i=1;i<=n;++i){
            par[i] = i;
        }
    }
    public static int find(int x){
        if(x!=par[x]) par[x]=find(par[x]);
        return par[x];
    }
    public static void unite(int a,int b){
        int aa = find(a);
        int bb = find(b);
        if(aa!=bb) {
            par[aa]=bb;
        }
    }
    public static int Kruskal(int m){
        int res = 0; //结果
        int cnt = 0; //记录边
        Arrays.sort(edges,0,m);
        for(int i=0;i<m;++i){
            int u = edges[i].u;
            int v = edges[i].v;
            int w = edges[i].w;
            if(find(u)!=find(v)){
                unite(u,v); //合并
                res+=w;
                cnt++;
            }
        }
        if(cnt<n-1) return INF; //若少于n-1条边，则说明图不连通
        else return res;
    }

    public static void main(String[] args) throws Exception {

        n = nextInt();
        int m = nextInt();
        init(n,m);
        for(int i=0;i<m;++i){
            int a = nextInt();
            int b = nextInt();
            int c = nextInt();
            edges[i] = new Edge(a,b,c);
        }

        int ans = Kruskal(m);
        cout.println(ans==INF? "orz":ans);
        cout.flush();
        closeAll();
    }

    public static void cinInit(){
        cin.wordChars('a', 'z');
        cin.wordChars('A', 'Z');
        cin.wordChars(128 + 32, 255);
        cin.whitespaceChars(0, ' ');
        cin.commentChar('/');
        cin.quoteChar('"');
        cin.quoteChar('\'');
        cin.parseNumbers(); //可单独使用来还原数字
    }

    public static int nextInt() throws Exception{
        cin.nextToken();
        return (int) cin.nval;
    }
    public static long nextLong() throws Exception{
        cin.nextToken();
        return (long) cin.nval;
    }
    public static double nextDouble() throws Exception{
        cin.nextToken();
        return cin.nval;
    }
    public static String nextString() throws Exception{
        cin.nextToken();
        return cin.sval;
    }
    public static void closeAll() throws Exception {
        cout.close();
        in.close();
        out.close();
    }

}

36、KMP 算法

判断模式串（p）是不是主串（s）的子串，返回主串中出现子串的下标
时间复杂度：O（n）
模式串p，主串s。字符串下标都是从1开始。n是p的长度，m是s的长度。
指针i指向主串，指针j指向模式串，每一轮是将i与j+1的位置比较，如果不满足，j就回退到ne[j]
如果i和j+1位置相同，那么就j++
一旦找到不符合的，我们就需要找前一位前面的子串的next数组（即 j+1 和 i 的位置比较）

static char[] p,s;//p是模式串，s是主串
static int[] ne = new int[N];//p的next数组,ne[i]=j表示相等的前后缀最大长度
//n是模式串的长度，m是主串的长度。

//1.计算模式串p的next数组（背过）
static void getNext() {
    for(int i=2,j=0;i<=n;i++) {
        while(j>0 && p[i]!=p[j+1]) 
            j=ne[j];
        if(p[i]==p[j+1])
            j++;
        ne[i] = j;
    }
}

//2.kmp匹配
for(int i=1,j=0;i<=m;i++) {
    while(j>0 && s[i]!=p[j+1])
        j=ne[j];
    if(s[i]==p[j+1]) j++;
    if(j==n) {//匹配成功
        out.print(i-n+1+" ");//下标从1开始
        j = ne[j];//计算后面是否还有子串p
    }
}

37、Prim 算法

适用于稠密图。时间复杂度：O(n^2)
核心思想：每次挑一条与当前集合相连的最短边。
最短边：取当前点和集合中所有点比较后的最短距离。
Prim 算法（朴素）

import java.io.*;
import java.math.BigInteger;
import java.util.*;

public class Main {
    public static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    public static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    public static StreamTokenizer cin = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    public static PrintWriter cout = new PrintWriter(new OutputStreamWriter(System.out));
    public static Scanner sc = new Scanner(System.in);

    public static int maxd = 200000+7;
    public static int INF = 0x3f3f3f3f;
    public static int mod = (int) 1e9+7;
    public static int[] dis = new int[maxd];
    public static int[] head = new int[maxd];
    public static int[] edgePre = new int[maxd<<1]; //无向图，边需要开2倍
    public static int[] edgeW = new int[maxd<<1];
    public static int[] edgeTo = new int[maxd<<1];
    public static boolean[] vis = new boolean[maxd];
    public static int n;
    public static int node=0;

    public static void add_edge(int a,int b,int c){
        edgeTo[node] = b;
        edgeW[node] = c;
        edgePre[node] = head[a];
        head[a]=node++;
    }

    public static void init(int n){
        for(int i=0;i<=n;++i){
            dis[i]=INF;
            vis[i]=false;
            head[i] = -1;
        }
    }
    public static int Prim(){//默认找到的第一个为集合的首元素
        int res = 0;
        for(int i=1;i<=n;++i){
            int t = -1;
            for(int j=1;j<=n;++j){
                if(!vis[j] && (t==-1 || dis[t]>dis[j]))
                    t = j;
            }
            vis[t]=true;
            if(i!=1 && dis[t]==INF) return INF; //当前点与集合中的所有点都不连通，不存在最小生成树
            if(i!=1) res+=dis[t]; //首元素不需要加
            for(int j=head[t];j!=-1;j=edgePre[j]){
                int to = edgeTo[j];
                dis[to] = Math.min(dis[to],edgeW[j]);
            }
        }
        return res;
    }


    public static void main(String[] args) throws Exception {

        n = nextInt();
        int m = nextInt();
        init(n);
        while(m-->0){
            int a = nextInt();
            int b = nextInt();
            int c = nextInt();
            add_edge(a,b,c); //无向图
            add_edge(b,a,c);
        }
        int ans = Prim();
        cout.println(ans==INF? "orz":ans);
        cout.flush();
        closeAll();
    }

    public static void cinInit(){
        cin.wordChars('a', 'z');
        cin.wordChars('A', 'Z');
        cin.wordChars(128 + 32, 255);
        cin.whitespaceChars(0, ' ');
        cin.commentChar('/');
        cin.quoteChar('"');
        cin.quoteChar('\'');
        cin.parseNumbers(); //可单独使用来还原数字
    }

    public static int nextInt() throws Exception{
        cin.nextToken();
        return (int) cin.nval;
    }
    public static long nextLong() throws Exception{
        cin.nextToken();
        return (long) cin.nval;
    }
    public static double nextDouble() throws Exception{
        cin.nextToken();
        return cin.nval;
    }
    public static String nextString() throws Exception{
        cin.nextToken();
        return cin.sval;
    }
    public static void closeAll() throws Exception {
        cout.close();
        in.close();
        out.close();
    }

}

Prim 算法（堆优化）
优化后时间复杂度为：时间复杂度 O(m*logn)

import java.io.*;
import java.math.BigInteger;
import java.util.*;


/**
 * @Author DragonOne
 * @Date 2021/12/5 21:27
 * @墨水记忆 www.tothefor.com
 */
public class Main {
    public static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    public static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    public static StreamTokenizer cin = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    public static PrintWriter cout = new PrintWriter(new OutputStreamWriter(System.out));
    public static Scanner sc = new Scanner(System.in);

    public static int maxd = 200000+7;
    public static int INF = 0x3f3f3f3f;
    public static int mod = (int) 1e9+7;
    public static int[] dis = new int[maxd];
    public static int[] head = new int[maxd];
    public static int[] edgePre = new int[maxd<<1]; //无向图，边需要开2倍
    public static int[] edgeW = new int[maxd<<1];
    public static int[] edgeTo = new int[maxd<<1];
    public static boolean[] vis = new boolean[maxd];
    public static int n;
    public static int node=0;

    public static class Edge implements Comparable<Edge> {
        private int to; //点
        private int w; //此点到集合的最短距离
        Edge(int to, int w) {
            this.to = to;
            this.w = w;
        }
        public int compareTo(Edge obj) {
            return this.w - obj.w;
        }
    }

    public static void add_edge(int a,int b,int c){
        edgeTo[node] = b;
        edgeW[node] = c;
        edgePre[node] = head[a];
        head[a]=node++;
    }

    public static void init(int n){
        for(int i=0;i<=n;++i){
            dis[i]=INF;
            vis[i]=false;
            head[i] = -1;
        }
    }
    public static int Prim(){
        PriorityQueue<Edge> q = new PriorityQueue<Edge>();
        int res = 0;
        int cnt = 0; //记录集合中的点数,只有等于给定点数n时才存在最小生成树，小于n则表示图不连通
        q.add(new Edge(1,0));
        while(!q.isEmpty()){
            Edge u = q.poll();
            if(vis[u.to]) continue;
            vis[u.to] = true;
            res+=u.w;
            cnt++;
            for(int i=head[u.to];i!=-1;i=edgePre[i]){
                if(dis[u.to]>edgeW[i]){
                    q.add(new Edge(edgeTo[i],edgeW[i]));
                }
            }
        }
        if(cnt<n) return INF; //集合中的点数小于给定点数，表示图不连通
        return res;
    }

    public static void main(String[] args) throws Exception {

        n = nextInt();
        int m = nextInt();
        init(n);
        while(m-->0){
            int a = nextInt();
            int b = nextInt();
            int c = nextInt();
            add_edge(a,b,c); //无向图
            add_edge(b,a,c);
        }
        int ans = Prim();
        cout.println(ans==INF? "orz":ans);
        cout.flush();
        closeAll();
    }

    public static void cinInit(){
        cin.wordChars('a', 'z');
        cin.wordChars('A', 'Z');
        cin.wordChars(128 + 32, 255);
        cin.whitespaceChars(0, ' ');
        cin.commentChar('/');
        cin.quoteChar('"');
        cin.quoteChar('\'');
        cin.parseNumbers(); //可单独使用来还原数字
    }

    public static int nextInt() throws Exception{
        cin.nextToken();
        return (int) cin.nval;
    }
    public static long nextLong() throws Exception{
        cin.nextToken();
        return (long) cin.nval;
    }
    public static double nextDouble() throws Exception{
        cin.nextToken();
        return cin.nval;
    }
    public static String nextString() throws Exception{
        cin.nextToken();
        return cin.sval;
    }
    public static void closeAll() throws Exception {
        cout.close();
        in.close();
        out.close();
    }

}

38、BellmanFord 算法

BellmanFord算法是一种图论中的算法，它用于计算单源最短路径问题，即从单一源点出发到所有其他节点的最短路径。与Dijkstra算法不同，BellmanFord算法能够处理包含负权边的图，但它无法处理包含负权环的图。
Bellman-Ford算法的时间复杂度为O(V*E)，其中V是顶点数，E是边数。这是因为算法需要松弛每一条边，并且最多需要松弛V-1轮。

import java.util.*;

public class BellmanFord {
    // 定义边类，包含源点、目标点和权重
    static class Edge {
        int src, dest, weight;
        public Edge(int src, int dest, int weight) {
            this.src = src; // 源点
            this.dest = dest; // 目标点
            this.weight = weight; // 边的权重
        }
    }

    // Bellman-Ford算法实现
    static void bellmanFord(ArrayList<Edge> edges, int V, int E, int src) {
        int[] dist = new int[V]; // 距离数组，用于存储从源点到每个点的最短距离

        // 初始化距离数组，将所有距离设置为无穷大，除了源点设置为0
        for (int i = 0; i < V; i++)
            dist[i] = Integer.MAX_VALUE;
        dist[src] = 0;

        // 松弛操作，进行V-1轮，每次对所有边进行松弛
        for (int i = 1; i < V; i++) {
            for (int j = 0; j < E; j++) {
                int u = edges.get(j).src; // 边的源点
                int v = edges.get(j).dest; // 边的目标点
                int weight = edges.get(j).weight; // 边的权重
                // 如果通过当前边可以使得目标点的距离更短，则更新距离
                if (dist[u] != Integer.MAX_VALUE && dist[u] + weight < dist[v])
                    dist[v] = dist[u] + weight;
            }
        }

        // 检测负权环，如果在完成V-1轮松弛后仍然可以松弛，则说明存在负权环
        for (int j = 0; j < E; j++) {
            int u = edges.get(j).src;
            int v = edges.get(j).dest;
            int weight = edges.get(j).weight;
            if (dist[u] != Integer.MAX_VALUE && dist[u] + weight < dist[v]) {
                System.out.println("图中存在负权环");
                return;
            }
        }

        // 输出最短路径，如果没有负权环，则dist数组中存储的就是最短路径长度
        for (int i = 0; i < V; i++)
            System.out.println(i + "\t\t" + dist[i]);
    }

    public static void main(String[] args) {
        int V = 5; // 图中的顶点数
        int E = 8; // 图中的边数
        ArrayList<Edge> edges = new ArrayList<>();

        // 添加边到边的列表中
        edges.add(new Edge(0, 1, -1));
        edges.add(new Edge(0, 2, 4));
        edges.add(new Edge(1, 2, 3));
        edges.add(new Edge(1, 3, 2));
        edges.add(new Edge(1, 4, 2));
        edges.add(new Edge(3, 2, 5));
        edges.add(new Edge(3, 1, 1));
        edges.add(new Edge(4, 3, -3));

        // 从源点0开始执行Bellman-Ford算法
        bellmanFord(edges, V, E, 0);
    }
}

39、LIS 最长公共子序列

public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int[] a1 = new int[n];
        int[] a2 = new int[m];
        int[][] dp = new int[n+1][m+1];
        for (int i = 0; i < n; i++) {
            a1[i]=sc.nextInt();
        }
        for (int i = 0; i < m; i++) {
            a2[i]=sc.nextInt();
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (a1[i-1]==a2[j-1]){
                    dp[i][j]=Math.max(dp[i-1][j-1]+1,dp[i][j]);
                }else {
                    dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        System.out.println(dp[n][m]);
    }

40、LCS最长上升子序列_朴素

适合输入数据小等于 1e5

int n = Int();
int[] arr = new int[n];
int[] dp1 = new int[n];
int[] dp2 = new int[n];
for (int i = 0; i < n; i++) {
    arr[i] = Int();
    dp1[i] = 1;
    dp2[i] = 1;
}
//从前往后LIS
for (int i = 1; i < n; i++) {
    for (int j = i; j > 0; j--) {
        if (arr[i] >= arr[j - 1]) {
            dp1[i] = Math.max(dp1[j - 1] + 1, dp1[i]);
        }
    }
}
//从后往前LIS
for (int i = n - 2; i >= 0; i--) {
    for (int j = i; j < n - 1; j++) {
        if (arr[i] >= arr[j + 1]) {
            dp2[i] = Math.max(dp2[j + 1] + 1, dp2[i]);
        }
    }
}
int max = 0;
for (int i = 0; i < n; i++) {
    max = Math.max(dp1[i] + dp2[i] - 1, max);
}
pw.println(n - max);  //维持左递增右递减至少需要出列多少个元素
pw.flush();

41、LCS最长上升子序列_二分

适合处理较大的输入数据

public static void main(String[] args) throws IOException{
    int n = Int();
    int[] f = new int[n+1];
    for (int i = 0; i < n; i++) {
        f[i]=Int();
    }
    int[] dp = new int[n+1];
    dp[0]=f[0];
    int cur = 0;
    for (int i = 1; i < n; i++) {
        if (f[i]>dp[cur]){
            dp[++cur]=f[i];
        }else {
            int idx = bs(dp,0,cur,f[i]);
            dp[idx]=f[i];
        }
    }
    pw.println(cur+1);
    pw.flush();
}

private static int bs(int[] dp, int l, int r, int t) {
    while (l<r){
        int mid = (l+r)/2;
        if (dp[mid]>=t){
            r = mid;
        }else {
            l = mid + 1;
        }
    }
    return r;
}

42、Manacher 算法

判断最长回文子串
计算字符串中每个位置作为回文中心的回文半径的算法，位置i的回文半径用p[i]表示，意思是在转换后的字符串中[i-p[i]+1,i+p[i]-1]是回文的
一般来说偶数长度是不会有回文中心的，因为没有意义。所以Mancher算法就是将原来的字符串变成有回文半径的字符串。可以通过添加字符，注意开头和结尾字符不一样！如ABBA->!#A#B#B#A#+

import java.math.BigInteger;
import java.util.*;
 
public class Main {
 
    public static void main(String[] args) {
        Scanner scanner=new Scanner(System.in);
        String s=scanner.next();
        System.out.println(mancher(s));
    }
    public static int mancher(String s){
        StringBuilder str=new StringBuilder();
        str.append('!');
        for(int i=0;i<s.length();i++){
            str.append('#');
            str.append(s.charAt(i));
        }
        str.append("#+");
        int[] p=new int[str.length()];
        //r：所有的回文子串中最大的右边界
        //c：对应的中心点
        int c=0,r=0,max=-1;
        for(int i=1;i<str.length()-1;i++){
            p[i]=i<r?Math.min(r-i,p[2*c-i]):1;
            while(str.charAt(p[i]+i)==str.charAt(i-p[i])){
                p[i]++;
            }
            if(p[i]+i>r){
                r=p[i]+i;
                c=i;
            }
            //真实的长度是p[i]-1，因为我们添加了字符，不是原来的字符串
            max=Math.max(p[i]-1,max);
        }
        return max;
    }
}

43、ST表_求区间最小值

ST表是一种用于解决RMQ（Range Minimum/Maximum Query，区间最小/最大值查询）问题的数据结构。它可以在O(nlogn)的时间复杂度内预处理，之后每次查询只需要O(1)的时间复杂度。

public class SparseTable {
    private int[][] st; // ST表，用于存储预处理的结果
    private int[] log; // 用于快速计算2的幂的对数
    private int n; // 数组的长度

    public SparseTable(int[] arr) {
        n = arr.length;
        int maxLog = 32 - Integer.numberOfLeadingZeros(n); // 计算最大的对数，用于确定ST表的大小
        st = new int[n][maxLog];
        log = new int[n + 1];

        // 初始化log数组，用于快速查询2的幂的对数
        for (int i = 2; i <= n; i++) {
            log[i] = log[i >> 1] + 1;
        }

        // 初始化ST表的第一行，即原数组
        for (int i = 0; i < n; i++) {
            st[i][0] = arr[i];
        }

        // 预处理ST表的其他行
        for (int j = 1; j < maxLog; j++) {
            for (int i = 0; i + (1 << j) <= n; i++) {
                // 对于每个区间，存储区间内的最小值
                st[i][j] = Math.min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
            }
        }
    }

    public int query(int l, int r) {
        int j = log[r - l + 1]; // 计算区间的长度对应的对数
        // 查询区间内的最小值
        return Math.min(st[l][j], st[r - (1 << j) + 1][j]);
    }

    public static void main(String[] args) {
        int[] arr = {3, 0, 1, 4, 2};
        SparseTable st = new SparseTable(arr);

        // 测试查询
        System.out.println(st.query(0, 3)); // 输出 0
        System.out.println(st.query(1, 4)); // 输出 1
    }
}

44、ST表_求区间最大值

- ST表是一种用于解决RMQ（Range Minimum/Maximum Query，区间最小/最大值查询）问题的数据结构。它可以在O(nlogn)的时间复杂度内预处理，之后每次查询只需要O(1)的时间复杂度。

public class SparseTable {
    private int[][] st; // ST表，用于存储预处理的结果
    private int[] log; // 用于快速计算2的幂的对数
    private int n; // 数组的长度

    public SparseTable(int[] arr) {
        n = arr.length;
        int maxLog = 32 - Integer.numberOfLeadingZeros(n); // 计算最大的对数，用于确定ST表的大小
        st = new int[n][maxLog];
        log = new int[n + 1];

        // 初始化log数组，用于快速查询2的幂的对数
        for (int i = 2; i <= n; i++) {
            log[i] = log[i >> 1] + 1;
        }

        // 初始化ST表的第一行，即原数组
        for (int i = 0; i < n; i++) {
            st[i][0] = arr[i];
        }

        // 预处理ST表的其他行
        for (int j = 1; j < maxLog; j++) {
            for (int i = 0; i + (1 << j) <= n; i++) {
                // 对于每个区间，存储区间内的最大值
                st[i][j] = Math.max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
            }
        }
    }

    public int query(int l, int r) {
        int j = log[r - l + 1]; // 计算区间的长度对应的对数
        // 查询区间内的最大值
        return Math.max(st[l][j], st[r - (1 << j) + 1][j]);
    }

    public static void main(String[] args) {
        int[] arr = {3, 0, 1, 4, 2};
        SparseTable st = new SparseTable(arr);

        // 测试查询
        System.out.println(st.query(0, 3)); // 输出 4
        System.out.println(st.query(1, 4)); // 输出 4
    }
}

45、并查集

并查集的模板，用于解决集合的合并与查找问题
并查集通常用于解决元素之间的连通性问题，比如在图论中判断两个节点是否在同一个连通分量中，或者在最小生成树算法中判断是否形成环等

    static int Maxn = 1e5+5;
    static int[] fa;
	private static void init(){	  //初始化每个节点的父节点为本身
        for(int i=0;i<Maxn;i++){
            fa[i]=i;
        }
	}
	
    private static void merge(int a, int b) {
        fa[find(a)]=find(b);  //将根节点a的父节点 设为根节点b
    }

    private static int find(int x) {
        if (fa[x]==x){  //如果x的父节点是本身 即为根节点
            return x;
        }else {
            fa[x]=find(fa[x]); //将父节点设置为根节点
            return fa[x]; //返回根节点
        }
    }

Maxn: 这是一个静态变量，用于表示并查集中元素的最大数量。
fa: 这是一个整型数组，用于存储每个元素的祖先（或代表元素）。
init(): 这个方法用于初始化并查集。它将每个元素的祖先设置为自己，即 fa[i] = i，这意味着一开始每个元素都是一个独立的集合。
merge(int a, int b): 这个方法用于合并两个集合。它首先找到代表元素 a 和 b
的根节点，然后将其中一个根节点的父节点设置为另一个，从而实现两个集合的合并。
find(int x): 这个方法用于查找元素 x 的根节点。如果 x 的父节点是本身（即 fa[x] == x），那么 x
就是根节点，直接返回 x。否则，它递归地查找 fa[x] 的根节点，并将 x
的父节点设置为这个根节点（这一步是路径压缩，用于优化后续的查找操作）。