1.理论基础

动态规划，英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。

所以动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的。

对于动态规划问题，拆解为如下五步曲：

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

2.裴波那契数

func fib(n int) int {
    if n<=1{
        return n
    }
    dp := make([]int,n+1)
    dp[0]=0
    dp[1]=1
    for i:=2;i<=n;i++{
        dp[i]=dp[i-1]+dp[i-2]
    }
    return dp[n] 
}

3.爬楼梯

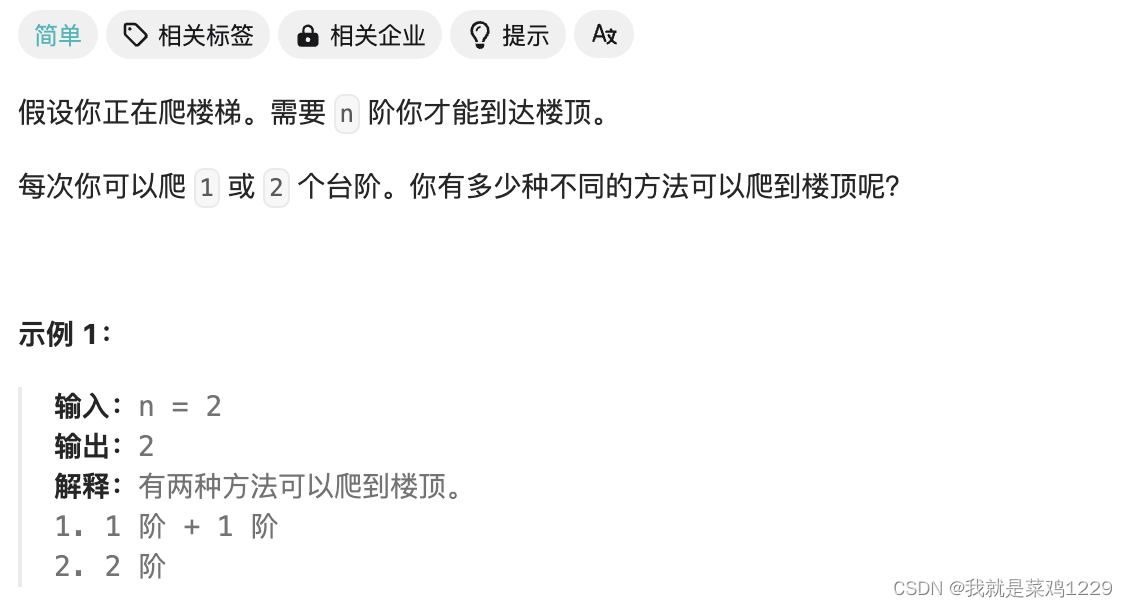
func climbStairs(n int) int {
    arr := make([]int,n+1)
    arr[0]=1
    arr[1]=1
    for i:=2;i<=n;i++{
        arr[i]=arr[i-1]+arr[i-2]
    }
    return arr[n]
}

4.使用最小花费爬楼梯

func minCostClimbingStairs(cost []int) int {
    n := len(cost)
    dp := make([]int,n+1)
    dp[0]=0
    dp[1]=0
    for i:=2;i<=n;i++{
        dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
    }
    return dp[n]
}

func min(a,b int)int{
    if a<b{
        return a
    }
    return b
}

5.不同路径

func uniquePaths(m int, n int) int {
	//初始化dp
	dp := make([][]int, m+1)
	for i := 0; i < m+1; i++ {
		dp[i] = make([]int, n+1)
	}
	dp[1][1] = 1
	//转移方程dp[i][j]=dp[i-1][j]+dp[i][j-1]
	for i := 1; i <= m; i++ {
		for j := 1; j <= n; j++ {
			if i==1&&j==1{
				continue
			}
			dp[i][j] = dp[i-1][j] + dp[i][j-1]
		}
	}
	return dp[m][n]
}

6.不同路径2

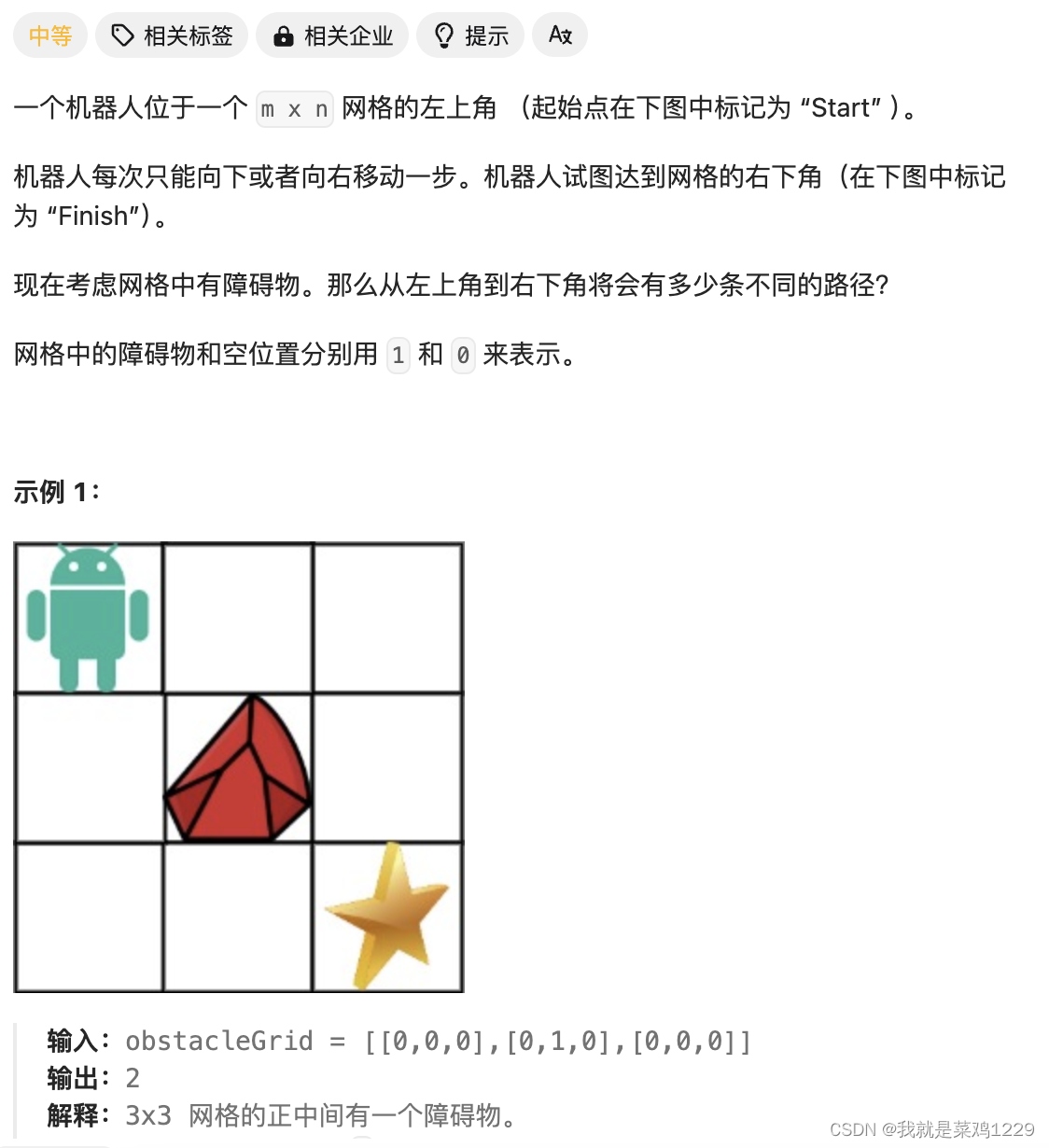
func uniquePathsWithObstacles(obstacleGrid [][]int) int {
    m,n := len(obstacleGrid),len(obstacleGrid[0])
    if obstacleGrid[0][0]==1{
        return 0
    }
    dp := make([][]int,m)
    for i:=0;i<m;i++{
        dp[i]=make([]int,n)
    }
    dp[0][0] = 1 
    for i:=0;i<m;i++{
        for j:=0;j<n;j++{
            left,up:=0,0
            if i==0&&j==0 || obstacleGrid[i][j]==1{
                continue
            }
            if i!=0&&obstacleGrid[i-1][j]!=1{
                up = dp[i-1][j]
            }
            if j!=0&&obstacleGrid[i][j-1]!=1{
                left = dp[i][j-1]
            }
            dp[i][j]=left+up
        }
    }
    return dp[m-1][n-1]
}

7.整数拆分

func integerBreak(n int) int {
    /**
    动态五部曲
    1.确定dp下标及其含义
    2.确定递推公式
    3.确定dp初始化
    4.确定遍历顺序
    5.打印dp
    **/
    dp := make([]int, n+1)
    dp[1] = 1
    dp[2] = 1
    for i:=3;i<n+1;i++{
        for j:=1;j<i-1;j++{
            //i可以拆分为i-j和j。由于需要最大值，故需要j遍历所有存在的值
            dp[i] = max(dp[i],max(j*(i-j),j*dp[i-j]))
        }
    }
    return dp[n]
}

func max(a, b int) int{
    if a > b {
        return a
    }
    return b
}

8.不同的二叉搜索树

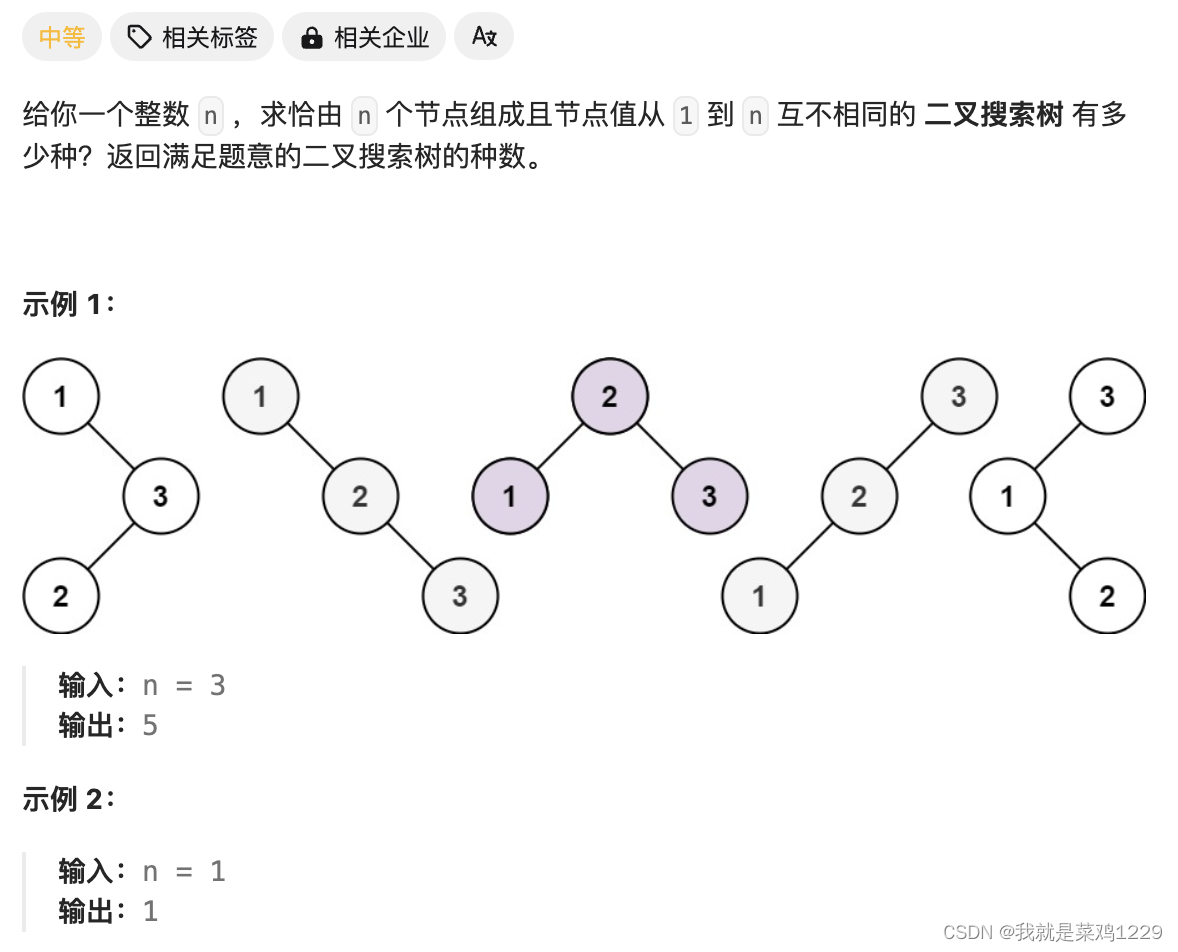
func numTrees(n int)int{
	dp := make([]int, n+1)
	dp[0] = 1
	for i := 1; i <= n; i++ {
		for j := 1; j <= i; j++ {
			dp[i] += dp[j-1] * dp[i-j]
		}
	}
	return dp[n]
}