分解质因数
题目:分解质因数
题目描述
给定一个正整数
n,编写一个程序将其分解为质因数,并按从小到大的顺序输出这些质因数。输入格式
一个正整数
n,其中n的范围是1 <= n <= 10^18。输出格式
按从小到大的顺序输出
n的质因数,每个质因数占一行。输入示例
4012100输出示例
2 5 53 757提示
程序需要处理大整数,因此使用
long long类型。质因数应该按从小到大的顺序输出。
每个质因数只输出一次,即使一个质因数在
n中出现多次。
一个任意的正整数 n 可以写成质因数的乘积形式: n = p 1 k 1 × p 2 k 2 × ⋯ × p m k m n=p1^{k1}×p2^{k2}×⋯×pm^{km} n=p1k1×p2k2×⋯×pmkm
其中, p 1 , p 2 , … , p p1,p2,…,p p1,p2,…,p 是质数, k 1 , k 2 , … , k k1,k2,…,k k1,k2,…,k 是对应的正整数指数。这个表示法称为整数的质因数分解。
2,3是最小的两个质数,用for循环从2开始遍历,一开始 t e m p = p 1 k 1 × p 2 k 2 × ⋯ × p m k m temp=p1^{k1}×p2^{k2}×⋯×pm^{km} temp=p1k1×p2k2×⋯×pmkm
每次遇到的temp%i==0,此时i表示的是其中一个质因数。
最开始的temp%i0,i2,i确实是质因数,接着把temp中有关2的因子全部除掉,接着循环。
如果temp%i==0,那么i一定是temp的质因子,首先i一定是temp的因子,那为什么是质因子呢?
如果i不是质数,说明比i小的一个数k是i的因子,那么之前i一定遍历过k,并且temp中把k的因子全部去掉,temp%i一定不等于0.
正是因为temp每次去掉所有的质因子,所以temp%i==0成立i一定是temp的质因子.
#include<bits/stdc++.h> // 包含所有标准库头文件
using namespace std;
#define int long long // 定义 int 为 long long 类型,方便处理大整数
#define _(i,a,b) for(int i=a;i<=b;i++) // 定义从 a 到 b 的循环
#define _1(i,a,b) for(int i=a;i>=b;i--) // 定义从 a 到 b 的反向循环
int n; // 定义全局变量 n
// 输入: 4012100
// 输出: 2, 5, 53, 757
vector<int> ret; // 用于存储质因数的向量
void solve() {
ret.clear(); // 清空存储质因数的向量
int temp = n; // 临时变量 temp 用于保存 n 的值
_(i, 2, n) { // 从 2 开始遍历到 n
if (i * i > temp) break; // 如果 i 的平方大于 temp,跳出循环
if (temp % i == 0) { // 如果 temp 能被 i 整除
ret.push_back(i); // 将 i 存入结果向量中
while (!(temp % i != 0)) { // 当 temp 能被 i 整除时
temp /= i; // 将 temp 除以 i
}
}
}
if (temp != 1) ret.push_back(temp); // 如果 temp 不等于 1,将 temp 存入结果向量
for (auto& x : ret) cout << x << endl; // 输出结果向量中的每个质因数
}
signed main() {
cin >> n; // 输入 n
solve(); // 调用求解函数
}
952. 按公因数计算最大组件大小
给定一个由不同正整数的组成的非空数组
nums,考虑下面的图:
有
nums.length个节点,按从nums[0]到nums[nums.length - 1]标记;只有当
nums[i]和nums[j]共用一个大于 1 的公因数时,nums[i]和nums[j]之间才有一条边。返回 图中最大连通组件的大小 。
示例 1:
输入: nums = [4,6,15,35] 输出: 4
示例 2:
输入: nums = [20,50,9,63] 输出: 2
示例 3:
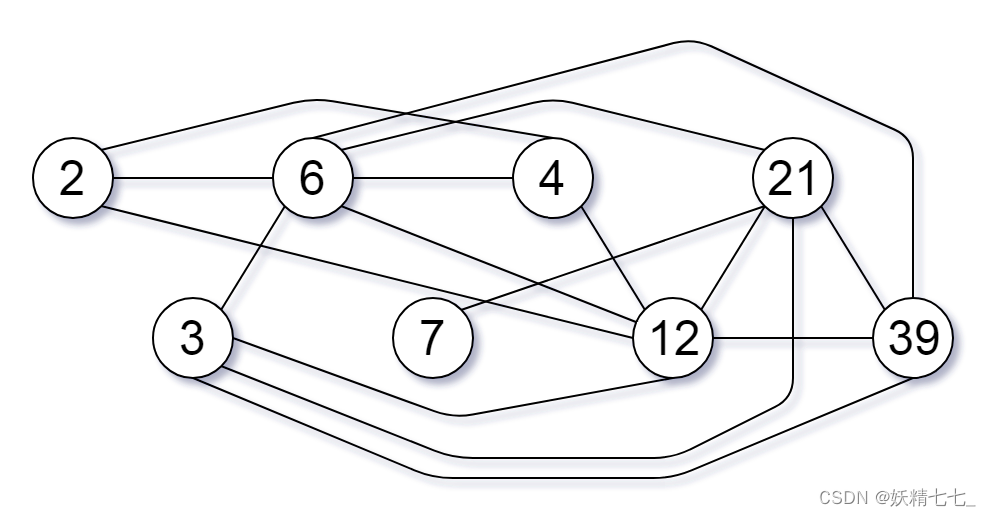
输入: nums = [2,3,6,7,4,12,21,39] 输出: 8
提示:
1 <= nums.length <= 2 * 10(4)
1 <= nums[i] <= 10(5)
nums中所有值都 不同
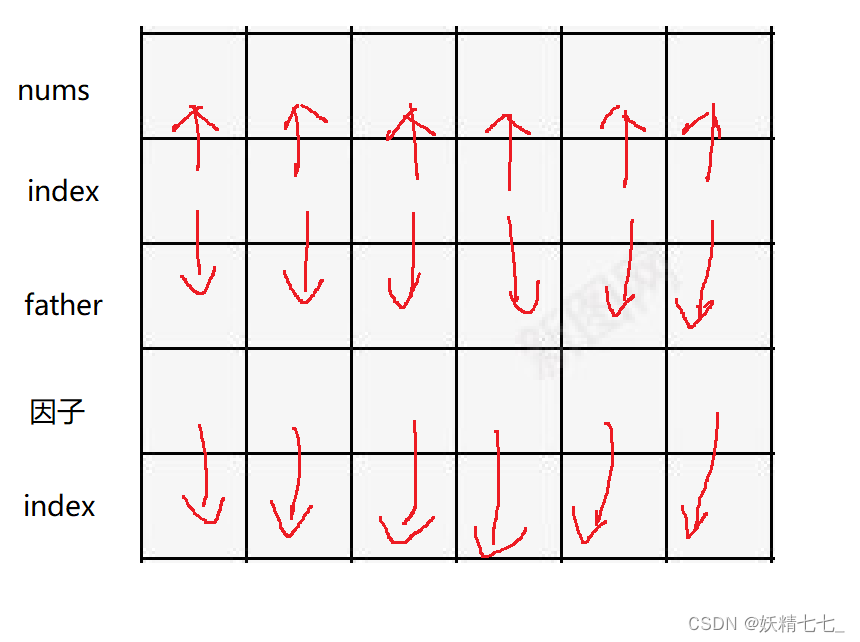
对于每一个数,我们可以分解质因数得到他的每一个质因数.
可以用map存储第一次拥有某个质因数的元素下标.
遍历nums数组,对于i位置元素,分解他的质因数,然后把i元素和他的质因数第一次出现的元素合并到一个集合里面.
并查集.
#define _(i, a, b) for (int i = a; i <= b; i++) // 定义一个从 a 到 b 的循环宏
#define _1(i, a, b) for (int i = a; i >= b; i--) // 定义一个从 a 到 b 的反向循环宏
class Solution {
public:
vector<int> nums; // 存储输入数组
int ret; // 存储结果,即最大连通组件的大小
vector<int> father; // 并查集的父节点数组
vector<int> sizee; // 并查集的大小数组
map<int, int> yinzi_index; // 存储质因数及其首次出现的索引
int n; // 存储输入数组的长度
// 并查集的查找函数
int findd(int i) {
if (father[i] != i) // 如果当前节点不是其自身的父节点
father[i] = findd(father[i]); // 递归查找其父节点,并进行路径压缩
return father[i]; // 返回父节点
}
// 并查集的合并函数
//并查集的合并函数,维护sizee和father数据,先计算x和y的代表节点下标,这样sizee和father谁先谁后都无所谓了.
//重要的是如果fx!=fy才需要维护sizee
void unionn(int x, int y) {
int fx = findd(x); // 查找 x 的父节点
int fy = findd(y); // 查找 y 的父节点
if (fx != fy) // 如果 x 和 y 的父节点不同
sizee[fy] += sizee[fx]; // 合并集合,并更新集合大小
father[fx] = father[fy]; // 将 x 的父节点指向 y 的父节点
}
// 核心解决函数
void solve() {
ret = 1; // 初始化结果为 1
n = nums.size(); // 获取输入数组的长度
yinzi_index.clear(); // 清空质因数索引的映射表
father.assign(n, 0), sizee.assign(n, 1); // 初始化并查集
_(i, 0, n - 1) { father[i] = i; } // 将每个节点的父节点指向其自身
// 遍历输入数组
_(i, 0, n - 1) {
//利用分解质因子的思维获取所有的质因子
int temp = nums[i]; // 获取当前元素
_(j, 2, nums[i]) { // 从 2 开始遍历到当前元素
if (j * j > temp) // 如果 j 的平方大于当前元素
break; // 跳出循环
if (temp % j == 0) { // 如果 j 是当前元素的因子
//对于i位置的元素,j是i的一个质因子
if (yinzi_index.count(j)) { // 如果 j 已经存在于质因数映射表中
//如果之前j质因子出现过,找到第一次出现的下标,然后合并
int index = yinzi_index[j]; // 获取 j 第一次出现的索引
unionn(index, i); // 合并当前元素和 j 第一次出现的元素
ret = max(ret, sizee[findd(i)]); // 更新最大连通组件的大小
} else {
//如果是第一次出现,那么就没有需要合并的元素.
yinzi_index[j] = i; // 将 j 的首次出现索引设置为当前索引
}
//分解质因数需要把确定的质因数全部去掉
while (!(temp % j != 0)) { // 将当前元素中所有 j 的因子去掉
temp /= j;
}
}
}
//对于i位置元素,如果temp!=1说明temp也是i的质因数,这一点不要忘记了.
if (temp != 1) { // 如果剩余部分不是 1,说明 temp 也是一个质因数
if (yinzi_index.count(temp)) { // 如果 temp 已经存在于质因数映射表中
int index = yinzi_index[temp]; // 获取 temp 第一次出现的索引
unionn(index, i); // 合并当前元素和 temp 第一次出现的元素
ret = max(ret, sizee[findd(i)]); // 更新最大连通组件的大小
} else {
yinzi_index[temp] = i; // 将 temp 的首次出现索引设置为当前索引
}
}
}
}
// 主函数,计算图中最大连通组件的大小
int largestComponentSize(vector<int>& _nums) {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 优化输入输出
nums = _nums; // 将输入数组赋值给成员变量
solve(); // 调用求解函数
return ret; // 返回结果
}
};
204. 计数质数
给定整数
n,返回 所有小于非负整数n的质数的数量 。示例 1:
输入: n = 10 输出: 4 解释: 小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
示例 2:
输入: n = 0 输出: 0
示例 3:
输入: n = 1 输出 :0
提示:
0 <= n <= 5 * 10(6)
for循环从2开始遍历,保证每一次i都可以判断是否是n的质因子.
第一次遇到的是质因子,然后把i所有的倍数设置为不是质数.
剪枝,如果当前i不是质数,那么i的倍数一定被设置完了.直接continue.
class Solution {
public:
int ret; // 存储质数的数量
vector<bool> visited; // 标记数组,用于标记非质数
int n; // 存储给定的上限数 n
void solve() {
visited.assign(n, false); // 初始化标记数组,初始时假设所有数都是质数
for(int i = 2; i < n; i++) { // 从 2 开始遍历到 n-1
if (!visited[i]) { // 如果当前数 i 没有被标记为非质数
ret++; // 说明 i 是质数,计数器增加
for (int j = i * 2; j < n; j += i) { // 标记所有 i 的倍数为非质数
visited[j] = true; // 标记 j 为非质数
}
}
}
}
int countPrimes(int _n) {
ios::sync_with_stdio(0), cout.tie(0), cin.tie(0); // 优化输入输出
n = _n; // 将输入的 n 赋值给成员变量 n
solve(); // 调用求解函数
return ret; // 返回质数的数量
}
};
结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!











![yarn dev报错X [ERROR] Cannot assign to “i“ because it is a constant](https://img-blog.csdnimg.cn/direct/1db99a1b9d7e4c2595e4a3e9ba6f0699.png)