引言

上一节介绍了玻尔兹曼机系列的相关模型，本节将介绍深度玻尔兹曼机的预训练过程。

深度信念网络预训练过程的问题

在玻尔兹曼机系列整体介绍中提到过，无论是深度信念网络还是深度玻尔兹曼机，它们建模的核心思想是：叠加$\text{RBM}$结构。以一个三层结构$v,h^{(1)},h^{(2)}$为例，观察未叠加时的状态表示如下：

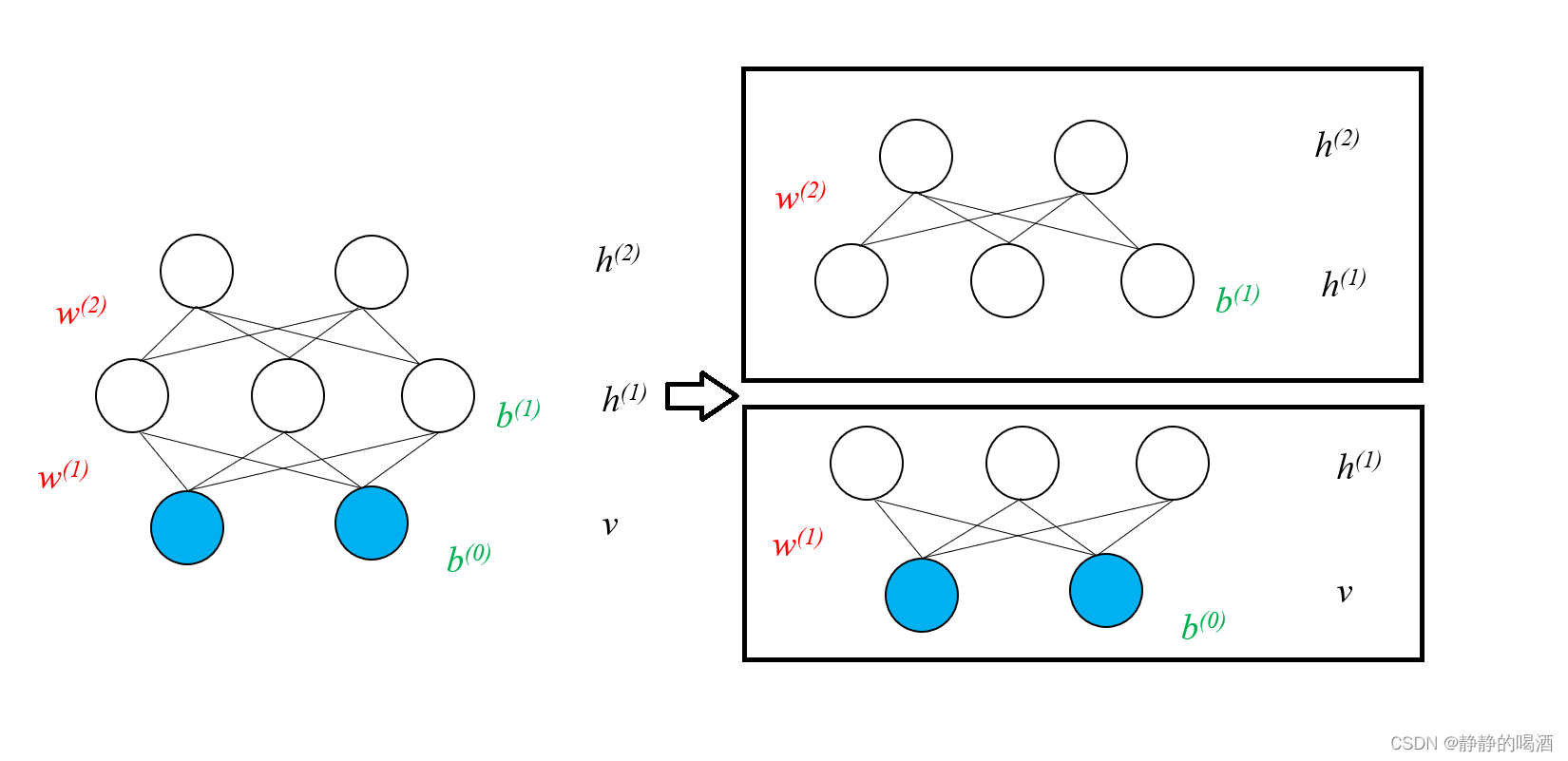
实际上，深度信念网络与深度玻尔兹曼机的学习过程是相同的。以深度信念网络为例，上图的学习过程可分为两个部分：
在受限玻尔兹曼机——对数似然梯度中介绍过，可以通过'对比散度'的方式求解模型参数的对数似然梯度，再通过梯度上升法对模型参数进行近似求解。在这里，求解模型参数并不是重点，只需要知道模型参数是可以求解的即可。

• 第一层学习过程：第一层本质上就是一个受限玻尔兹曼机，关于观测变量的似然函数$\mathcal{P}(v)$可表示如下:
  $$\mathcal{P}(v)=\sum _{h^{(1)}}\mathcal{P}(v,h^{(1)})=\sum _{h^{(1)}}\mathcal{P}(h^{(1)})\cdot \mathcal{P}(v\mid h^{(1)})$$
  关于两个概率分布$\mathcal{P}(h^{(1)}),\mathcal{P}(v\mid h^{(1)})$在玻尔兹曼机系列整体介绍中提到过，它们均可以通过模型参数进行表示：

  • $\mathcal{P}(h^{(1)})$可表示为如下形式：
    关于‘联合概率分布’$\mathcal{P}(v,h^{(1)})$详见受限玻尔兹曼机——模型表示
    这里为方便观看起见，暂时将各随机变量与自身关联关系对应的偏置项$b,c$忽略掉。
    $$\begin{array}{rl}\mathcal{P}(h^{(1)})& =\sum _v\mathcal{P}(v,h^{(1)})\\ & =\sum _v\frac{1}{\mathcal{Z}}\exp [v^T{\mathcal{W}}^{(1)}\cdot h^{(1)}]\end{array}$$
  • $\mathcal{P}(v\mid h^{(1)})$根据受限玻尔兹曼机——后验概率可表示为如下形式：
    $$\begin{array}{rl}\mathcal{P}(v\mid h^{(1)})& =\prod _{k=1}^{|\mathcal{D}|}\mathcal{P}(v_k\mid h^{(1)})\\ \mathcal{P}(v_k\mid h^{(1)})& =\text{Sigmoid}\left(\sum _{j=1}^{|\mathcal{P}|}{w}_{k}j\cdot h_j+b_k\right)w_{kj}\in {\mathcal{W}}^{(1)}\end{array}$$

  这里仅需要知道$\mathcal{P}(h^{(1)}),\mathcal{P}(v\mid h^{(1)})$可以使用${\mathcal{W}}^{(1)}$进行表示即可，这里使用符号$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)}),\mathcal{P}(v\mid h^{(1)};{\mathcal{W}}^{(1)})$进行表示：
  第一层学习过程的重点在于：边缘概率分布$\mathcal{P}(h^{(1)})$仅和模型参数${\mathcal{W}}^{(1)}$之间存在关联关系。
  $$\mathcal{P}(v;{\mathcal{W}}^{(1)})=\sum _{h^{(1)}}\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})\cdot \mathcal{P}(v\mid h^{(1)};{\mathcal{W}}^{(1)})$$

• 第二层学习过程，第二层同样也是一个受限玻尔兹曼机，如果是处理方式，和第一层是完全相同的。但第二层需要的样本是关于$h^{(1)}$随机变量结点相关的样本，而我们只有观测变量$v$的样本$\mathcal{V}$。
  因此，必然需要关于$h^{(1)}$的样本。因而需要从第一层的后验$\mathcal{P}(h^{(1)}\mid v)$中采集样本。关于后验$\mathcal{P}(h^{(1)}\mid v)$表示如下：
  受限玻尔兹曼机各隐变量之间相互条件独立，这是受限玻尔兹曼机自身的结构性质。
  $$\mathcal{P}(h^{(1)}\mid v)=\prod _{l=1}^{|{\mathcal{P}}^{(1)}|}\mathcal{P}(h_l\mid v)$$
  关于隐变量集合$h^{(1)}$中的某一个隐变量$h_l$的后验分布表示如下。通过对该概率分布进行采样，可以得到关于$\mathcal{P}(h_l\mid v)$的样本信息。
  $$\mathcal{P}(h_l\mid v)=\{\begin{array}{l}\text{Sigmoid}\left({\sum }_{i=1}^n{w}_{li}\cdot v_i+c_l\right)h_l=1\\ 1-\text{Sigmoid}\left({\sum }_{i=1}^n{w}_{li}\cdot v_i+c_l\right)h_l=0\end{array}$$
  至此，有了关于$h^{(1)}$的样本之后，可以和第一层学习过程一样，对第二层的隐变量$h^{(2)}$进行表示：
  和第一层的过程相同，这里不再赘述。
  $$\begin{array}{rl}\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})& =\sum _{h^{(2)}}\mathcal{P}(h^{(1)},h^{(2)};{\mathcal{W}}^{(2)})\\ & =\sum _{h^{(2)}}\mathcal{P}(h^{(2)};{\mathcal{W}}^{(2)})\cdot \mathcal{P}(h^{(1)}\mid h^{(2)};{\mathcal{W}}^{(2)})\end{array}$$

在深度信念网络中，它将上述两层受限玻尔兹曼机堆叠的过程中，它仅仅是将$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})$通过新构建一层模型，从而构成新的受限玻尔兹曼机进行学习。从公式的角度观察，它将$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})$替换了$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})$：
$$\begin{array}{rl}\text{DBN : }\mathcal{P}(v;{\mathcal{W}}^{(1)})& =\sum _{h^{(1)}}\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})\cdot \mathcal{P}(v\mid h^{(1)};{\mathcal{W}}^{(1)})\\ & =\sum _{h^{(1)}}\left[\sum _{h^{(2)}}\mathcal{P}(h^{(2)};{\mathcal{W}}^{(2)})\cdot \mathcal{P}(h^{(1)}\mid h^{(2)};{\mathcal{W}}^{(2)})\right]\cdot \mathcal{P}(v\mid h^{(1)};{\mathcal{W}}^{(1)})\end{array}$$
但在3层网络中，也就是第一层第二层合并的情况下，关于隐变量集合$h^{(1)}$的 真实后验 是什么？在混合后的3层网络中，边缘概率分布$\mathcal{P}(h^{(1)})$表示如下：
$$\mathcal{P}(h^{(1)})=\sum _{h^{(2)},v}\mathcal{P}(v,h^{(1)},h^{(2)})$$
虽然此时没有办法写出该网络的联合概率分布表示，但不可否认的是，$\mathcal{P}(v,h^{(1)},h^{(2)})$必然和参数${\mathcal{W}}^{(1)},{\mathcal{W}}^{(2)}$均有关联：
$$\mathcal{P}(h^{(1)})\Rightarrow \mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)},{\mathcal{W}}^{(2)})$$
也就是说，深度信念网络仅用包含${\mathcal{W}}^{(2)}$的表示近似了真实表示：
$$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})\approx \mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)},{\mathcal{W}}^{(2)})$$
此时，在两个受限玻尔兹曼机叠加之后，无论是单个受限玻尔兹曼机的$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})$还是深度信念网络的$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})$，它们的表示 都是不准确的。能否存在一个想法，让$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})$和$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})$联合在一起去近似$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)},{\mathcal{W}}^{(2)})$呢？

深度玻尔兹曼机的预训练过程(2023/1/24)

针对上述问题，存在这样一个想法：既然想要联合近似，可以将$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})$和$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})$对应取算数平均值：
$$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)},{\mathcal{W}}^{(2)})\approx \frac{1}{2}\left[\mathcal{P}(h^{(1)}\mid {\mathcal{W}}^{(1)})+\mathcal{P}(h^{(1)}\mid {\mathcal{W}}^{(2)})\right]$$
这种说法并非绝对，算数平均值仅是一种具体操作，而背后的思想是：相比于深度信念网络$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})\approx \mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)},{\mathcal{W}}^{(2)})$，能否在两个受限玻尔兹曼机结合在一起后，关于边缘概率分布$\mathcal{P}(h^{(1)})$的描述让${\mathcal{W}}^{(1)}$也参与进来，而不是仅使用${\mathcal{W}}^{(2)}$进行描述。

虽然受限玻尔兹曼机对模型结构存在严苛要求，但这些要求主要影响的是观测变量、隐变量之间的关系，对应的是条件概率$\mathcal{P}(h^{(1)}\mid v^{(1)})$或者$\mathcal{P}(v^{(1)}\mid h^{(1)})$。这意味着条件概率能够被准确表示。

但边缘概率分布$\mathcal{P}(h^{(1)})$并不能被精确表示，而只能被近似表示。观察$\mathcal{P}(h^{(1)})$的展开式，可以通过蒙特卡洛方法进行近似：

• 关于${\sum }_{v^{(1)}}$内包含$N$个，也就是样本数量个连加项，可看作计算代价为∞，而针对这种期望形式的表达，使用蒙特卡洛方法近似是完全可以实现的。
• 关于$\frac{1}{N}{\sum }_{v^{(i)}\in \mathcal{V}}\mathcal{P}(h^{(1)}\mid v^{(i)};{\mathcal{W}}^{(1)})$这种求解方式也被称作$\text{appregated posterior Distribution}$聚合后验分布，后验自然是指$\mathcal{P}(h^{(1)}\mid v^{(i)};{\mathcal{W}}^{(1)})$,而聚合是指：本想从‘真实分布’${\mathcal{P}}_{data}/\mathcal{P}(v^{(1)})$中进行采样，但实际上，真实分布是无法得到的，而只有$N$个真实样本，通过$N$个真实样本的‘经验分布’作为采样分布来近似${\mathcal{P}}_{data}$.

$$\begin{array}{rl}\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})& =\sum _{v^{(1)}}\mathcal{P}(v^{(1)},h^{(1)};{\mathcal{W}}^{(1)})\\ & =\sum _{v^{(1)}}\mathcal{P}(v^{(1)})\cdot \mathcal{P}(h^{(1)}\mid v^{(1)};{\mathcal{W}}^{(1)})\\ & ={\mathbb{E}}_{\mathcal{P}(v^{(1)})}\left[\mathcal{P}(h^{(1)}\mid v^{(1)};{\mathcal{W}}^{(1)})\right]\\ & \approx \frac{1}{N}\sum _{v^{(i)}\in \mathcal{V}}\mathcal{P}(h^{(1)}\mid v^{(i)};{\mathcal{W}}^{(1)})\end{array}$$
同理，关于参数${\mathcal{W}}^{(2)}$表示的边缘概率分布$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})$使用蒙特卡洛方法表示为：
其中$\mathcal{H}$表示从$\mathcal{P}(h^{(2)})$中采样所产生的样本集合。不同于$\mathcal{P}(v^{(1)})$中的具体样本，准确的说，它是经过两次迭代采样得到的样本：
$$\begin{array}{r}\mathcal{P}(h^{(1)})\Leftarrow {\left\{h^{(1),i}\right\}}_{i=1}^N\sim \mathcal{P}(h^{(1)}\mid v^{(1)};{\mathcal{W}}^{(1)})\end{array}$$

• 上述是第一层产生的样本。很明显，它是从后验分布$\mathcal{P}(h^{(1)}\mid v^{(1)};{\mathcal{W}}^{(1)})$中采集出来的，但真正想要的是$\mathcal{P}(h^{(1)})$自身的分布。而$\mathcal{P}(h^{(1)})$分布和$\mathcal{P}(v^{(1)})$一样，没有办法求出准确解。因此，将采样得到的 { h ( 1 ) , i } i = 1 N \{h^{(1),i}\}_{i=1}^N {h(1),i}i=1N​所形成的经验分布近似为 $\mathcal{P}(h^{(1)})$.
  $$\mathcal{P}(h^{(2)})\Leftarrow {\left\{h^{(2),j}\right\}}_{j=1}^N=\mathcal{H}\sim \mathcal{P}(h^{(2)}\mid h^{(1)};{\mathcal{W}}^{(2)})$$
• 此时已经得到了$h^{(1)}$的样本，上述描述的是以相同方法产生的第二层样本。

$$\begin{array}{rl}\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})& =\sum _{h^{(2)}}\mathcal{P}(h^{(1)},h^{(2)};{\mathcal{W}}^{(2)})\\ & =\sum _{h^{(2)}}\mathcal{P}(h^{(2)})\cdot \mathcal{P}(h^{(1)}\mid h^{(2)};{\mathcal{W}}^{(2)})\\ & ={\mathbb{E}}_{\mathcal{P}(h^{(2)})}\left[\mathcal{P}(h^{(1)}\mid h^{(2)};{\mathcal{W}}^{(2)})\right]\\ & \approx \frac{1}{N}\sum _{h^{(2)}\in \mathcal{H}}\mathcal{P}(h^{(1)}\mid h^{(2)};{\mathcal{W}}^{(2)})\end{array}$$

此时，两个网络层关于$\mathcal{P}(h^{(1)})$的聚合后验分布表示结束后，在两网络层融合过程中，关于$\mathcal{P}(h^{(1)})$的描述以算术平均值为例，可能得到如下结果：
这仅仅描述的是通过不同参数得到的聚合后验分布的融合过程。
$$\begin{array}{rl}\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)};{\mathcal{W}}^{(2)})& \approx \frac{1}{2}\left[\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})+\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})\right]\\ & =\frac{1}{2N}\left[\sum _{v^{(i)}\in \mathcal{V}}\mathcal{P}(h^{(1)}\mid v^{(i)};{\mathcal{W}}^{(1)})+\sum _{h^{(2)}\in \mathcal{H}}\mathcal{P}(h^{(2)}\mid h^{(1)};{\mathcal{W}}^{(2)})\right]\end{array}$$
这种模型融合的方式是否存在问题：这种相加的方式会存在$\text{Double Counting}$现象。在上面的描述中，样本集合$\mathcal{V}$和$h^{(2)}$对应的样本集合$\mathcal{H}$之间并不是相互独立的，而是通过$\text{bottom-up}$方法逐级生成出来的：
$$\begin{array}{rl}\mathcal{V}& \Rightarrow \underset{近似计算\mathcal{P}(h^{(1)})}{\underbrace{\frac{1}{N}\sum _{v^{(i)}\in \mathcal{V}}\mathcal{P}(h^{(1)}\mid v^{(i)};{\mathcal{W}}^{(1)})\approx \mathcal{P}(h^{(1)})}}\\ & \Rightarrow \underset{从\mathcal{P}(h^{(1)})中抽取样本，组成关于h^{(1)}的隐变量样本集合\hat{\mathcal{H}}}{\underbrace{\hat{\mathcal{H}}={\left\{h^{(1),i}\right\}}_{i=1}^N\sim \mathcal{P}(h^{(1)})}}\\ & \Rightarrow \underset{近似计算\mathcal{P}(h^{(2)})}{\underbrace{\frac{1}{N}\sum _{h^{(1)\in \hat{\mathcal{H}}}}\mathcal{P}(h^{(2)}\mid h^{(1)};{\mathcal{W}}^{(2)})\approx \mathcal{P}(h^{(2)})}}\\ & \Rightarrow \underset{从\mathcal{P}(h^{(2)})中抽取样本，组成关于h^{(2)}的因变量样本集合\mathcal{H}}{\underbrace{\mathcal{H}={\left\{h^{(2),j}\right\}}_{j=1}^N\sim \mathcal{P}(h^{(2)})}}\end{array}$$
很明显可以观察到：

• 计算$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})$时，需要使用隐变量样本集合$\mathcal{H}$；隐变量样本集合$\mathcal{H}$生成过程中，就已经用过样本集合$\mathcal{V}$一次；
• 计算$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})$时，需要使用样本集合$\mathcal{V}$，此时又用了一次；

这意味着样本集合$\mathcal{V}$被重复使用了。这种操作会产生什么影响：会使得该模型表达的分布过于尖锐。何为尖锐？即样本分布极差很大。为何会产生这种情况？因为假设通过采样得到了两个完全相同的样本，即便他们在样本空间中重合，那也是两个样本，而样本集合在描述概率分布过程中，使用的是 经验分布，在重复使用样本集合$\mathcal{V}$时整个经验分布会产生严重的数值上的分裂：

• 数据密集的部分可能会影响较小(概率密度函数下降的程度较小)，或者说经验分布分子、分母之间比率相差不大；
• 而数据不密集的部分会有较大影响，虽然分子数值上升，但远没有分母增加的多，这使得概率密度函数相比之前更小了。
• 这种分布可能没有缓冲区间，对应模型产生的生成样本，也会存在特征上的较大缺陷。

相关参考：
深度玻尔兹曼机2-预训练1-介绍