目录
一、快速排序核心思想
二、快速排序步骤
(1)暴力做法
(2)双指针做法
三、代码模板
四、边界问题
五、总结
一、快速排序核心思想
分治,即将一个序列划分成左部分小于等于x,右部分大于等于x
二、快速排序步骤
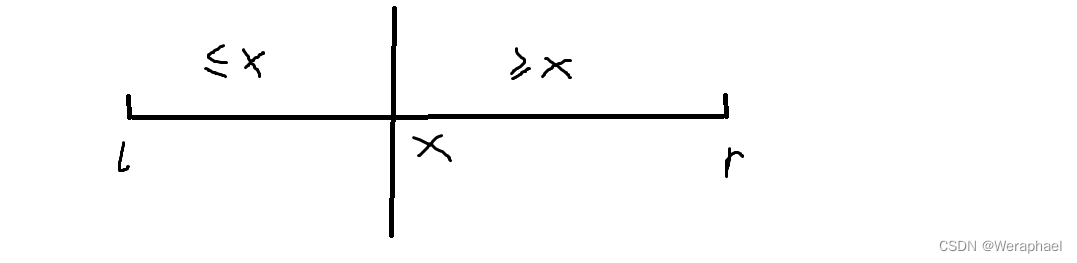
①确定一个分界点x。分界点可以是左端 a[l]、右端a[r]、中间值a[(l+r) / 2]、以及随机取值。
②调整区间。将数组一分为二,使≤x在左边,≥x在右边。【重点】
③递归处理左右两个部分。
Q:如何将数组一分为二,使≤x在左边,≥x在右边呢?
(1)、暴力做法:
1> 开辟两个数组从c[ ]、b[ ]。
2>将原数组a[ ]中把≤x的元素放在c[ ]中,≥x放在b[ ]中。
3>最后将c[ ] 放入 a[ ],c[ ]放入a[ ]。
(2)、双指针做法(推荐)
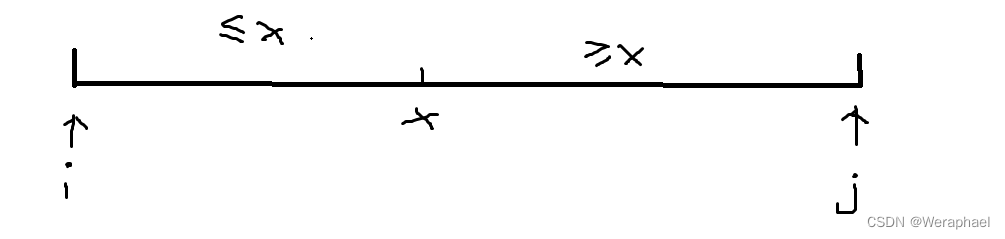
首先先让指针 i++ 向中间寻找元素,直到指向的元素 ≥x 停下
同样地,再将指针 j - -向中间寻找元素,直到指向的元素 ≤x 停下
当条件满足 i < j,就将这两个元素交换
最终指针 j 就一定会在指针 i 的前面
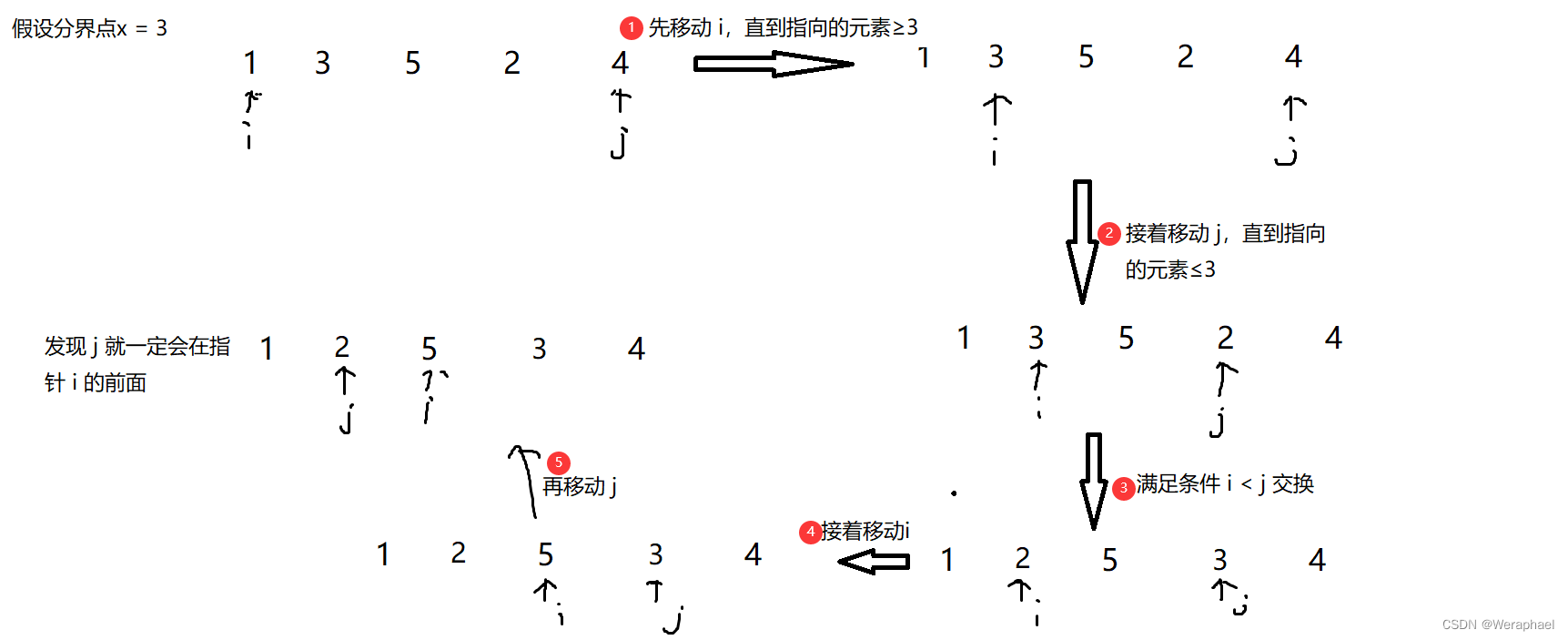
举个例子,如下图所示
三、代码模板
void quick_sort(int a[],int l,int r)
{
if(l >= r) return; //如果数组中就一个数,就已经排好了(递归出口)
int x = a[(l + r) / 2]; //确定分界点
int i = l - 1,j = r + 1;
while (i < j)
{
do i++; while(a[i] < x);
do j--; while(a[j] > x);
if (i < j) swap(a[i],a[j]);
}
//递归处理左部分
quick_sort(a,l,j);
//递归处理右部分
quick_sort(a,j + 1,r);
}四、边界问题
①为什么要使用 do while循环而while循环
while(a[i] < x) i++;
while(a[i] > x) j--;如图所示,假设数组中有相同的元素,会死循环

②为什么移动移动 i 和 j的条件分别是 < x 和 > x,而不是一开始所说的 <= x 和 >= x
如果分界点x,恰好是数组中最大值,会导致 i++ 越界。
同理,如果分界点又恰好是数组中最小值,也会导致 j -- 越界。
③当x=a[l]
递归部分就不能使用quick_sort(a,l,i - 1)、quick_sort(a,i,r)
假设数组只有1和2在排序时,假设分界点x = 1,因此 到时候 i 和 j 会同时指向1,对于第一个递归quick_sort(a,0,- 1),相当于没有值,也就没有交换,但到了第二个递归quick_sort(a,0,2),就一直就这两个数交换,导致了死递归
④当x = a[r]
递归部分就不能使用quick_sort(a,l,j)、quick_sort(a,j + 1,r)
例子和①一样
⑤当x=a[(l + r) /2]
同样的道理,假设数组中只有2个元素分别是1和2,这时,分界点x = 1,这种情况和③类似,就不能使用quick_sort(a,l,i - 1)、quick_sort(a,i,r)
⑥当x=a[(l + r + 1) / 2]
递归部分就不能使用quick_sort(a,l,j)、quick_sort(a,j + 1,r)
五、总结
(1)当x=a[l] 或者 x=a[(l + r) /2],只能用quick_sort(a, l, j); //左半部分递归 quick_sort(a,j + 1, r); //右半部分递归(2)当x=q[r] or x=q[l+r + 1>>1],只能用
quick_sort(a,l,i - 1);//左半部分递归 quick_sort(a, i, r);//右半部分递归