介绍
排序算法是计算机科学中被广泛研究的一个课题。历时多年,它发展出了数十种算法,这些
算法都着眼于一个问题:如何将一个无序的数字数组整理成升序?先来学习一些“简单排序”,它们很好懂,但效率不如其他排序算法。主打一个循序渐进👏
冒泡排序🐳
假设要对[4, 2, 7, 1, 3]进行排序。它现在是无序的,我们的目标是产生一个包含相同元素、升序的数组。
第 1 步:首先,比较 4 和 2。如图可见它们的顺序是错的

第 2 步:交换它们的位置
第 3 步:比较 4 和 7:

依次类推,每一次轮回过后,未排序的值中最大的那个都会“冒”到正确的位置上。
用python实现
def bubble_sort(list):
unsorted_until_index = len(list) - 1
sorted = False
while not sorted:
sorted = True
for i in range(unsorted_until_index):
if list[i] > list[i+1]:
sorted = False
list[i], list[i+1] = list[i+1], list[i]
unsorted_until_index = unsorted_until_index - 1
list = [65, 55, 45, 35, 25, 15, 10]
bubble_sort(list)
print(list)
输出:
[10, 15, 25, 35, 45, 55, 65]
效率
冒泡排序的执行步骤可分为两种。
- 比较:比较两个数看哪个更大。
- 交换:交换两个数的位置以使它们按顺序排列
如果数组不只是随机打乱,而是完全反序,在这种最坏的情况下,每次比较过后都得进行一
次交换。
现在把两种步骤放在一起来看。一个含有 10 个元素的数组,需要:
9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45 次比较,以及 45 次交换,共 90 步。
效率太低了😓。元素量呈倍数增长,步数却呈指数增长,如下表所示:

因此描述冒泡排序效率的大 O 记法,是 O(N 2)。
规范一些来说:用 O(N 2)算法处理 N 个元素,大约需要 N 2步。
O(N 2)算法是比较低效的,随着数据量变多,其步数也剧增,如下图所示:
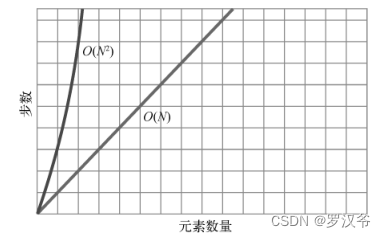
- 嵌套循环
function hasDuplicateValue(array) {
var steps = 0;
for (var i = 0; i < array.length; i++) {
for (var j = 0; j < array.length; j++) {
steps++;
if (i !== j && array[i] == array[j]) {
return true;
}
}
}
console.log(steps);
return false;
}
hasDuplicateValue([1,2,3])
嵌套循环算法的效率就是 O(N^2)。一旦看到嵌套循环,你就应该马上想到 O(N2)
改进
以下时间复杂度:其大 O 记法是 O(N)
function hasDup(array){
var steps = 0;
var existsNumbers = [];
for (let i = 0; i < array.length; i++) {
steps++;
if(existsNumbers[array[i]]===undefined){
existsNumbers[array[i]] = 1;
}else{
return true;
}
}
console.log(steps);
return false;
}
执行 hasDuplicateValue([1,2,3])的话,你会看到输出为 3,跟元素个数一致。
选择排序👈
冒泡排序算法,其效率是 O(N 2)。现在我们再来探索另一种排序算法,选择排序:
步骤
(1) 从左至右检查数组的每个格子,找出值最小的那个。在此过程中,我们会用一个变量来记住检查过的数字的最小值(事实上记住的是索引,但为了看起来方便,下图就直接写出数值)。
如果一个格子中的数字比记录的最小值还要小,就把变量改成该格子的索引。

(2) 知道哪个格子的值最小之后,将该格与本次检查的起点交换。第 1 次检查的起点是索引 0,第2此起点时索引1

(3) 重复第(1) (2)步,直至数组排好序
效率
选择排序的步骤可分为两类:比较和交换,也就是在每轮检查中把未排序的值跟该轮已遇到的最小值做比较,以及将最小值与该轮起点的值交换以使其位置正确。
但每轮的交换最多只有 1 次。如果该轮的最小值已在正确位置,就无须交换,否则要做 1 次交换。相比之下,冒泡排序在最坏情况(完全逆序)时,每次比较过后都要进行 1 次交换。

选择排序的大 O 记法为 O(N2),跟冒泡排序一样!🙋
因为:大 O 记法不包含一般数字,除非是指数。
例如:当数据量少于某个值时,O(N2)是比 O(100N)要快的,但过了这个值之后,O(100N)便反超 O(N 2),并一直保持优势!
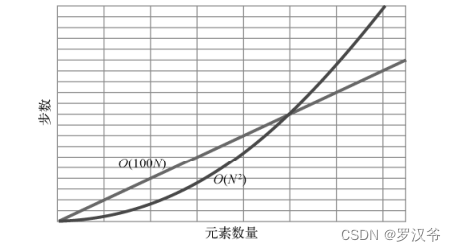
这就是大 O 记法忽略常数的原因。大 O 记法只表明,对于不同分类,存在一临界点,在这
一点之后,一类算法会快于另一类,并永远保持下去。至于这个点在哪里,大 O 并不关心。
插入排序✍
我们已经学过两种排序算法:冒泡排序和选择排序。虽然它们的效率都是 O(N 2),但其实选择排序比冒泡排序快一倍。现在来学第三种排序算法——插入排序。
在最坏的情况里,插入排序的时间复杂度跟冒泡排序、选择排序一样,都是 O(N2)
效率
插入排序包含 4 种步骤:移除、比较、平移和插入。要分析插入算法的效率,就得把每种步骤都统计一遍。
在数组完全逆序的最坏情况下,我们每一轮都要将 temp_value 左侧的所有值与temp_value 比较。因为那些值全都大于 temp_value,所以每一轮都要等到空隙移到最左端才能结束。
在第一轮,temp_value 为索引 1 的值,由于 temp_value 左侧只有一个值,所以最多进行一次比较。到了第二轮,最多进行两次比较,以此类推。到最后一轮时,就要拿 temp_value 以外的所有值与其进行比较。换言之,如果数组有 N 个元素,则最后一轮中最多进行 N - 1 次比较。

总结
懂得区分最好、平均、最坏情况,是为当前场景选择最优算法以及给现有算法调优以适应环
境变化的关键。记住,虽然为最坏情况做好准备十分重要,但大部分时间我们面对的是平均情况。